CUDA Shared Memory Bank

   blog 15 minutes read (About 2243 words)  visits

Introduction

Memory bank is a key concept for CUDA shared memory. To get the best performance out of a CUDA kernel implementation, the user will have to pay attention to memory bank access and avoid memory bank access conflicts.

In this blog post, I would like to quickly discuss memory bank for CUDA shared memory.

Memory Bank

Memory Bank Properties

To achieve high memory bandwidth for concurrent accesses, shared memory is divided into equally sized memory modules (banks) that can be accessed simultaneously. Therefore, any memory load or store of $n$ addresses that spans $n$ distinct memory banks can be serviced simultaneously, yielding an effective bandwidth that is $n$ times as high as the bandwidth of a single bank.

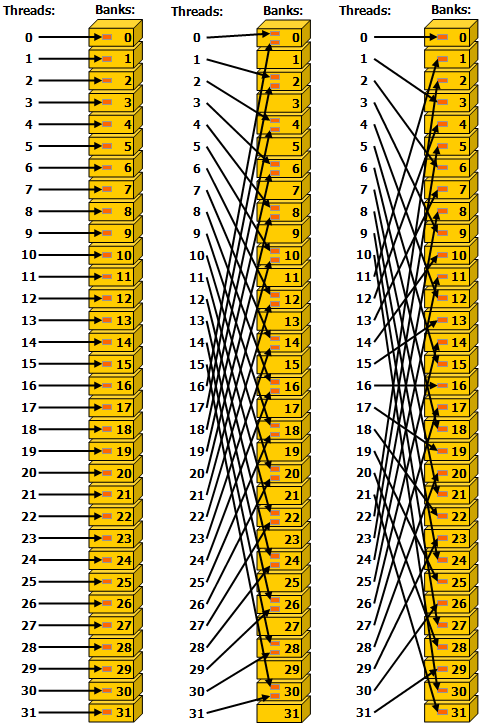
However, if multiple addresses of a memory request map to the same memory bank, the accesses are serialized. The hardware splits a memory request that has bank conflicts into as many separate conflict-free requests as necessary, decreasing the effective bandwidth by a factor equal to the number of separate memory requests. The one exception here is when multiple threads in a warp address the same shared memory location, resulting in a broadcast. In this case, multiple broadcasts from different banks are coalesced into a single multicast from the requested shared memory locations to the threads.

Memory Bank Mapping

The memory bank properties were described above. However, how memory addresses map to memory banks is architecture-specific.

On devices of compute capability 5.x or newer, each bank has a bandwidth of 32 bits every clock cycle, and successive 32-bit words are assigned to successive banks. The warp size is 32 threads and the number of banks is also 32, so bank conflicts can occur between any threads in the warp.

To elaborate on this, let’s see how memory addresses map to memory banks using examples. The following program illustrated the idea of 1D and 2D memory address to memory banks mapping for devices of compute capability 5.x or newer.

memory_bank.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <memory>
#include <vector>

template <typename T>
void bank_id_1d_mapping(int bank_size, int num_banks, int N)
{
    for (int i{0}; i < N; ++i)
    {
        // bank_size: Bank size in bits.
        // 8: 8 bits per Byte.
        int bank_idx = (i * sizeof(T) * 8 / bank_size) % num_banks;
        std::cout << "Array Idx: " << i << " "
                  << "Bank Idx: " << bank_idx << std::endl;
    }
}

template <typename T>
void bank_id_2d_mapping(int bank_size, int num_banks, int M, int N)
{
    for (int i{0}; i < M; ++i)
    {
        for (int j{0}; j < N; ++j)
        {
            int bank_idx =
                ((i * N + j) * sizeof(T) * 8 / bank_size) % num_banks;
            std::cout << "Matrix Idx: (" << i << ", " << j << ") "
                      << "Bank Idx: " << bank_idx << std::endl;
        }
    }
}

int main()
{

    constexpr const int bank_size{32}; // bits
    constexpr const int num_banks{32};

    const int M{4};
    const int N{32};

    std::cout << "Bank ID Mapping 1D: N = " << N << std::endl;
    bank_id_1d_mapping<float>(bank_size, num_banks, N);
    std::cout << "Bank 2D Mapping 1D: M = " << M << " N = " << N << std::endl;
    bank_id_2d_mapping<float>(bank_size, num_banks, M, N);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
$ g++ memory_bank.cpp -o memory_bank -std=c++14
$ ./memory_bank
Bank ID Mapping 1D: N = 32
Array Idx: 0 Bank Idx: 0
Array Idx: 1 Bank Idx: 1
Array Idx: 2 Bank Idx: 2
Array Idx: 3 Bank Idx: 3
Array Idx: 4 Bank Idx: 4
Array Idx: 5 Bank Idx: 5
Array Idx: 6 Bank Idx: 6
Array Idx: 7 Bank Idx: 7
Array Idx: 8 Bank Idx: 8
Array Idx: 9 Bank Idx: 9
Array Idx: 10 Bank Idx: 10
Array Idx: 11 Bank Idx: 11
Array Idx: 12 Bank Idx: 12
Array Idx: 13 Bank Idx: 13
Array Idx: 14 Bank Idx: 14
Array Idx: 15 Bank Idx: 15
Array Idx: 16 Bank Idx: 16
Array Idx: 17 Bank Idx: 17
Array Idx: 18 Bank Idx: 18
Array Idx: 19 Bank Idx: 19
Array Idx: 20 Bank Idx: 20
Array Idx: 21 Bank Idx: 21
Array Idx: 22 Bank Idx: 22
Array Idx: 23 Bank Idx: 23
Array Idx: 24 Bank Idx: 24
Array Idx: 25 Bank Idx: 25
Array Idx: 26 Bank Idx: 26
Array Idx: 27 Bank Idx: 27
Array Idx: 28 Bank Idx: 28
Array Idx: 29 Bank Idx: 29
Array Idx: 30 Bank Idx: 30
Array Idx: 31 Bank Idx: 31
Bank 2D Mapping 1D: M = 4 N = 32
Matrix Idx: (0, 0) Bank Idx: 0
Matrix Idx: (0, 1) Bank Idx: 1
Matrix Idx: (0, 2) Bank Idx: 2
Matrix Idx: (0, 3) Bank Idx: 3
Matrix Idx: (0, 4) Bank Idx: 4
Matrix Idx: (0, 5) Bank Idx: 5
Matrix Idx: (0, 6) Bank Idx: 6
Matrix Idx: (0, 7) Bank Idx: 7
Matrix Idx: (0, 8) Bank Idx: 8
Matrix Idx: (0, 9) Bank Idx: 9
Matrix Idx: (0, 10) Bank Idx: 10
Matrix Idx: (0, 11) Bank Idx: 11
Matrix Idx: (0, 12) Bank Idx: 12
Matrix Idx: (0, 13) Bank Idx: 13
Matrix Idx: (0, 14) Bank Idx: 14
Matrix Idx: (0, 15) Bank Idx: 15
Matrix Idx: (0, 16) Bank Idx: 16
Matrix Idx: (0, 17) Bank Idx: 17
Matrix Idx: (0, 18) Bank Idx: 18
Matrix Idx: (0, 19) Bank Idx: 19
Matrix Idx: (0, 20) Bank Idx: 20
Matrix Idx: (0, 21) Bank Idx: 21
Matrix Idx: (0, 22) Bank Idx: 22
Matrix Idx: (0, 23) Bank Idx: 23
Matrix Idx: (0, 24) Bank Idx: 24
Matrix Idx: (0, 25) Bank Idx: 25
Matrix Idx: (0, 26) Bank Idx: 26
Matrix Idx: (0, 27) Bank Idx: 27
Matrix Idx: (0, 28) Bank Idx: 28
Matrix Idx: (0, 29) Bank Idx: 29
Matrix Idx: (0, 30) Bank Idx: 30
Matrix Idx: (0, 31) Bank Idx: 31
Matrix Idx: (1, 0) Bank Idx: 0
Matrix Idx: (1, 1) Bank Idx: 1
Matrix Idx: (1, 2) Bank Idx: 2
Matrix Idx: (1, 3) Bank Idx: 3
Matrix Idx: (1, 4) Bank Idx: 4
Matrix Idx: (1, 5) Bank Idx: 5
Matrix Idx: (1, 6) Bank Idx: 6
Matrix Idx: (1, 7) Bank Idx: 7
Matrix Idx: (1, 8) Bank Idx: 8
Matrix Idx: (1, 9) Bank Idx: 9
Matrix Idx: (1, 10) Bank Idx: 10
Matrix Idx: (1, 11) Bank Idx: 11
Matrix Idx: (1, 12) Bank Idx: 12
Matrix Idx: (1, 13) Bank Idx: 13
Matrix Idx: (1, 14) Bank Idx: 14
Matrix Idx: (1, 15) Bank Idx: 15
Matrix Idx: (1, 16) Bank Idx: 16
Matrix Idx: (1, 17) Bank Idx: 17
Matrix Idx: (1, 18) Bank Idx: 18
Matrix Idx: (1, 19) Bank Idx: 19
Matrix Idx: (1, 20) Bank Idx: 20
Matrix Idx: (1, 21) Bank Idx: 21
Matrix Idx: (1, 22) Bank Idx: 22
Matrix Idx: (1, 23) Bank Idx: 23
Matrix Idx: (1, 24) Bank Idx: 24
Matrix Idx: (1, 25) Bank Idx: 25
Matrix Idx: (1, 26) Bank Idx: 26
Matrix Idx: (1, 27) Bank Idx: 27
Matrix Idx: (1, 28) Bank Idx: 28
Matrix Idx: (1, 29) Bank Idx: 29
Matrix Idx: (1, 30) Bank Idx: 30
Matrix Idx: (1, 31) Bank Idx: 31
Matrix Idx: (2, 0) Bank Idx: 0
Matrix Idx: (2, 1) Bank Idx: 1
Matrix Idx: (2, 2) Bank Idx: 2
Matrix Idx: (2, 3) Bank Idx: 3
Matrix Idx: (2, 4) Bank Idx: 4
Matrix Idx: (2, 5) Bank Idx: 5
Matrix Idx: (2, 6) Bank Idx: 6
Matrix Idx: (2, 7) Bank Idx: 7
Matrix Idx: (2, 8) Bank Idx: 8
Matrix Idx: (2, 9) Bank Idx: 9
Matrix Idx: (2, 10) Bank Idx: 10
Matrix Idx: (2, 11) Bank Idx: 11
Matrix Idx: (2, 12) Bank Idx: 12
Matrix Idx: (2, 13) Bank Idx: 13
Matrix Idx: (2, 14) Bank Idx: 14
Matrix Idx: (2, 15) Bank Idx: 15
Matrix Idx: (2, 16) Bank Idx: 16
Matrix Idx: (2, 17) Bank Idx: 17
Matrix Idx: (2, 18) Bank Idx: 18
Matrix Idx: (2, 19) Bank Idx: 19
Matrix Idx: (2, 20) Bank Idx: 20
Matrix Idx: (2, 21) Bank Idx: 21
Matrix Idx: (2, 22) Bank Idx: 22
Matrix Idx: (2, 23) Bank Idx: 23
Matrix Idx: (2, 24) Bank Idx: 24
Matrix Idx: (2, 25) Bank Idx: 25
Matrix Idx: (2, 26) Bank Idx: 26
Matrix Idx: (2, 27) Bank Idx: 27
Matrix Idx: (2, 28) Bank Idx: 28
Matrix Idx: (2, 29) Bank Idx: 29
Matrix Idx: (2, 30) Bank Idx: 30
Matrix Idx: (2, 31) Bank Idx: 31
Matrix Idx: (3, 0) Bank Idx: 0
Matrix Idx: (3, 1) Bank Idx: 1
Matrix Idx: (3, 2) Bank Idx: 2
Matrix Idx: (3, 3) Bank Idx: 3
Matrix Idx: (3, 4) Bank Idx: 4
Matrix Idx: (3, 5) Bank Idx: 5
Matrix Idx: (3, 6) Bank Idx: 6
Matrix Idx: (3, 7) Bank Idx: 7
Matrix Idx: (3, 8) Bank Idx: 8
Matrix Idx: (3, 9) Bank Idx: 9
Matrix Idx: (3, 10) Bank Idx: 10
Matrix Idx: (3, 11) Bank Idx: 11
Matrix Idx: (3, 12) Bank Idx: 12
Matrix Idx: (3, 13) Bank Idx: 13
Matrix Idx: (3, 14) Bank Idx: 14
Matrix Idx: (3, 15) Bank Idx: 15
Matrix Idx: (3, 16) Bank Idx: 16
Matrix Idx: (3, 17) Bank Idx: 17
Matrix Idx: (3, 18) Bank Idx: 18
Matrix Idx: (3, 19) Bank Idx: 19
Matrix Idx: (3, 20) Bank Idx: 20
Matrix Idx: (3, 21) Bank Idx: 21
Matrix Idx: (3, 22) Bank Idx: 22
Matrix Idx: (3, 23) Bank Idx: 23
Matrix Idx: (3, 24) Bank Idx: 24
Matrix Idx: (3, 25) Bank Idx: 25
Matrix Idx: (3, 26) Bank Idx: 26
Matrix Idx: (3, 27) Bank Idx: 27
Matrix Idx: (3, 28) Bank Idx: 28
Matrix Idx: (3, 29) Bank Idx: 29
Matrix Idx: (3, 30) Bank Idx: 30
Matrix Idx: (3, 31) Bank Idx: 31

Memory Bank Conflicts

Notice that for 2D matrix, assuming the data type bitwidth is 32 bit, if $N$ is a multiple of 32, the elements in the same column of the matrix belongs to the same memory bank. This is where memory bank conflicts can easily happen in the implementation. If the threads in a warp try to access the values in the same column of the matrix, there will be severe memory bank conflicts. Using some other values for $N$, such as 33, can avoid the elements in the same column of the matrix belongs to the same memory bank. So be careful about the stride of memory bank access.

memory_bank.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <memory>
#include <vector>

template <typename T>
void bank_id_1d_mapping(int bank_size, int num_banks, int N)
{
    for (int i{0}; i < N; ++i)
    {
        int bank_idx = (i * sizeof(T) * 8 / bank_size) % num_banks;
        std::cout << "Array Idx: " << i << " "
                  << "Bank Idx: " << bank_idx << std::endl;
    }
}

template <typename T>
void bank_id_2d_mapping(int bank_size, int num_banks, int M, int N)
{
    for (int i{0}; i < M; ++i)
    {
        for (int j{0}; j < N; ++j)
        {
            int bank_idx =
                ((i * N + j) * sizeof(T) * 8 / bank_size) % num_banks;
            std::cout << "Matrix Idx: (" << i << ", " << j << ") "
                      << "Bank Idx: " << bank_idx << std::endl;
        }
    }
}

int main()
{

    constexpr const int bank_size{32}; // bits
    constexpr const int num_banks{32};

    const int M{4};
    const int N{33};

    std::cout << "Bank ID Mapping 1D: N = " << N << std::endl;
    bank_id_1d_mapping<float>(bank_size, num_banks, N);
    std::cout << "Bank 2D Mapping 1D: M = " << M << " N = " << N << std::endl;
    bank_id_2d_mapping<float>(bank_size, num_banks, M, N);
}

In practice, the additional column is unused and can be filled with any value. Just to make sure that the algorithm implemented will not produce incorrect results by accidentally using the values that are not supposed to be used in the additional column.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
$ g++ memory_bank.cpp -o memory_bank -std=c++14
$ ./memory_bank
Bank ID Mapping 1D: N = 33
Array Idx: 0 Bank Idx: 0
Array Idx: 1 Bank Idx: 1
Array Idx: 2 Bank Idx: 2
Array Idx: 3 Bank Idx: 3
Array Idx: 4 Bank Idx: 4
Array Idx: 5 Bank Idx: 5
Array Idx: 6 Bank Idx: 6
Array Idx: 7 Bank Idx: 7
Array Idx: 8 Bank Idx: 8
Array Idx: 9 Bank Idx: 9
Array Idx: 10 Bank Idx: 10
Array Idx: 11 Bank Idx: 11
Array Idx: 12 Bank Idx: 12
Array Idx: 13 Bank Idx: 13
Array Idx: 14 Bank Idx: 14
Array Idx: 15 Bank Idx: 15
Array Idx: 16 Bank Idx: 16
Array Idx: 17 Bank Idx: 17
Array Idx: 18 Bank Idx: 18
Array Idx: 19 Bank Idx: 19
Array Idx: 20 Bank Idx: 20
Array Idx: 21 Bank Idx: 21
Array Idx: 22 Bank Idx: 22
Array Idx: 23 Bank Idx: 23
Array Idx: 24 Bank Idx: 24
Array Idx: 25 Bank Idx: 25
Array Idx: 26 Bank Idx: 26
Array Idx: 27 Bank Idx: 27
Array Idx: 28 Bank Idx: 28
Array Idx: 29 Bank Idx: 29
Array Idx: 30 Bank Idx: 30
Array Idx: 31 Bank Idx: 31
Array Idx: 32 Bank Idx: 0
Bank 2D Mapping 1D: M = 4 N = 33
Matrix Idx: (0, 0) Bank Idx: 0
Matrix Idx: (0, 1) Bank Idx: 1
Matrix Idx: (0, 2) Bank Idx: 2
Matrix Idx: (0, 3) Bank Idx: 3
Matrix Idx: (0, 4) Bank Idx: 4
Matrix Idx: (0, 5) Bank Idx: 5
Matrix Idx: (0, 6) Bank Idx: 6
Matrix Idx: (0, 7) Bank Idx: 7
Matrix Idx: (0, 8) Bank Idx: 8
Matrix Idx: (0, 9) Bank Idx: 9
Matrix Idx: (0, 10) Bank Idx: 10
Matrix Idx: (0, 11) Bank Idx: 11
Matrix Idx: (0, 12) Bank Idx: 12
Matrix Idx: (0, 13) Bank Idx: 13
Matrix Idx: (0, 14) Bank Idx: 14
Matrix Idx: (0, 15) Bank Idx: 15
Matrix Idx: (0, 16) Bank Idx: 16
Matrix Idx: (0, 17) Bank Idx: 17
Matrix Idx: (0, 18) Bank Idx: 18
Matrix Idx: (0, 19) Bank Idx: 19
Matrix Idx: (0, 20) Bank Idx: 20
Matrix Idx: (0, 21) Bank Idx: 21
Matrix Idx: (0, 22) Bank Idx: 22
Matrix Idx: (0, 23) Bank Idx: 23
Matrix Idx: (0, 24) Bank Idx: 24
Matrix Idx: (0, 25) Bank Idx: 25
Matrix Idx: (0, 26) Bank Idx: 26
Matrix Idx: (0, 27) Bank Idx: 27
Matrix Idx: (0, 28) Bank Idx: 28
Matrix Idx: (0, 29) Bank Idx: 29
Matrix Idx: (0, 30) Bank Idx: 30
Matrix Idx: (0, 31) Bank Idx: 31
Matrix Idx: (0, 32) Bank Idx: 0
Matrix Idx: (1, 0) Bank Idx: 1
Matrix Idx: (1, 1) Bank Idx: 2
Matrix Idx: (1, 2) Bank Idx: 3
Matrix Idx: (1, 3) Bank Idx: 4
Matrix Idx: (1, 4) Bank Idx: 5
Matrix Idx: (1, 5) Bank Idx: 6
Matrix Idx: (1, 6) Bank Idx: 7
Matrix Idx: (1, 7) Bank Idx: 8
Matrix Idx: (1, 8) Bank Idx: 9
Matrix Idx: (1, 9) Bank Idx: 10
Matrix Idx: (1, 10) Bank Idx: 11
Matrix Idx: (1, 11) Bank Idx: 12
Matrix Idx: (1, 12) Bank Idx: 13
Matrix Idx: (1, 13) Bank Idx: 14
Matrix Idx: (1, 14) Bank Idx: 15
Matrix Idx: (1, 15) Bank Idx: 16
Matrix Idx: (1, 16) Bank Idx: 17
Matrix Idx: (1, 17) Bank Idx: 18
Matrix Idx: (1, 18) Bank Idx: 19
Matrix Idx: (1, 19) Bank Idx: 20
Matrix Idx: (1, 20) Bank Idx: 21
Matrix Idx: (1, 21) Bank Idx: 22
Matrix Idx: (1, 22) Bank Idx: 23
Matrix Idx: (1, 23) Bank Idx: 24
Matrix Idx: (1, 24) Bank Idx: 25
Matrix Idx: (1, 25) Bank Idx: 26
Matrix Idx: (1, 26) Bank Idx: 27
Matrix Idx: (1, 27) Bank Idx: 28
Matrix Idx: (1, 28) Bank Idx: 29
Matrix Idx: (1, 29) Bank Idx: 30
Matrix Idx: (1, 30) Bank Idx: 31
Matrix Idx: (1, 31) Bank Idx: 0
Matrix Idx: (1, 32) Bank Idx: 1
Matrix Idx: (2, 0) Bank Idx: 2
Matrix Idx: (2, 1) Bank Idx: 3
Matrix Idx: (2, 2) Bank Idx: 4
Matrix Idx: (2, 3) Bank Idx: 5
Matrix Idx: (2, 4) Bank Idx: 6
Matrix Idx: (2, 5) Bank Idx: 7
Matrix Idx: (2, 6) Bank Idx: 8
Matrix Idx: (2, 7) Bank Idx: 9
Matrix Idx: (2, 8) Bank Idx: 10
Matrix Idx: (2, 9) Bank Idx: 11
Matrix Idx: (2, 10) Bank Idx: 12
Matrix Idx: (2, 11) Bank Idx: 13
Matrix Idx: (2, 12) Bank Idx: 14
Matrix Idx: (2, 13) Bank Idx: 15
Matrix Idx: (2, 14) Bank Idx: 16
Matrix Idx: (2, 15) Bank Idx: 17
Matrix Idx: (2, 16) Bank Idx: 18
Matrix Idx: (2, 17) Bank Idx: 19
Matrix Idx: (2, 18) Bank Idx: 20
Matrix Idx: (2, 19) Bank Idx: 21
Matrix Idx: (2, 20) Bank Idx: 22
Matrix Idx: (2, 21) Bank Idx: 23
Matrix Idx: (2, 22) Bank Idx: 24
Matrix Idx: (2, 23) Bank Idx: 25
Matrix Idx: (2, 24) Bank Idx: 26
Matrix Idx: (2, 25) Bank Idx: 27
Matrix Idx: (2, 26) Bank Idx: 28
Matrix Idx: (2, 27) Bank Idx: 29
Matrix Idx: (2, 28) Bank Idx: 30
Matrix Idx: (2, 29) Bank Idx: 31
Matrix Idx: (2, 30) Bank Idx: 0
Matrix Idx: (2, 31) Bank Idx: 1
Matrix Idx: (2, 32) Bank Idx: 2
Matrix Idx: (3, 0) Bank Idx: 3
Matrix Idx: (3, 1) Bank Idx: 4
Matrix Idx: (3, 2) Bank Idx: 5
Matrix Idx: (3, 3) Bank Idx: 6
Matrix Idx: (3, 4) Bank Idx: 7
Matrix Idx: (3, 5) Bank Idx: 8
Matrix Idx: (3, 6) Bank Idx: 9
Matrix Idx: (3, 7) Bank Idx: 10
Matrix Idx: (3, 8) Bank Idx: 11
Matrix Idx: (3, 9) Bank Idx: 12
Matrix Idx: (3, 10) Bank Idx: 13
Matrix Idx: (3, 11) Bank Idx: 14
Matrix Idx: (3, 12) Bank Idx: 15
Matrix Idx: (3, 13) Bank Idx: 16
Matrix Idx: (3, 14) Bank Idx: 17
Matrix Idx: (3, 15) Bank Idx: 18
Matrix Idx: (3, 16) Bank Idx: 19
Matrix Idx: (3, 17) Bank Idx: 20
Matrix Idx: (3, 18) Bank Idx: 21
Matrix Idx: (3, 19) Bank Idx: 22
Matrix Idx: (3, 20) Bank Idx: 23
Matrix Idx: (3, 21) Bank Idx: 24
Matrix Idx: (3, 22) Bank Idx: 25
Matrix Idx: (3, 23) Bank Idx: 26
Matrix Idx: (3, 24) Bank Idx: 27
Matrix Idx: (3, 25) Bank Idx: 28
Matrix Idx: (3, 26) Bank Idx: 29
Matrix Idx: (3, 27) Bank Idx: 30
Matrix Idx: (3, 28) Bank Idx: 31
Matrix Idx: (3, 29) Bank Idx: 0
Matrix Idx: (3, 30) Bank Idx: 1
Matrix Idx: (3, 31) Bank Idx: 2
Matrix Idx: (3, 32) Bank Idx: 3

Here is an example of memory conflicts due to inappropriate strides.

Memory Bank Access of Stride = 1, 2, and 3 in a Warp

References

CUDA Shared Memory Bank

https://leimao.github.io/blog/CUDA-Shared-Memory-Bank/

Author

Lei Mao

Posted on

06-22-2022

Updated on

08-19-2022

Licensed under

 

Like this article? Support the author with

Comments

  Follow   Sponsor

Catalogue

×