Prefix-Free Code and Huffman Coding
Introduction
Prefix-free code and Huffman coding are concepts in information theory, but I actually know little in this field. The first time I heard about Huffman coding was actually in the Deep Learning class where the professor was trying to prove the “Source Coding Theorem” using prefix-free codes. Frankly, I did not understand too much about the theory, but prefix-free code and Huffman coding turn out to be quite useful in some deep learning tasks, such as a Huffman tree hierarchical softmax. So I need to at least understand the basic concept of prefix-free code and try to construct a Huffman tree on my own.
Prefix-Free Code
Prefix-free code and prefix code are actually the same things (forget about how the namings were done). The formal definition of a prefix-free code system from Wikipedia is as follows:
“A prefix code is a type of code system (typically a variable-length code) distinguished by its possession of the “prefix property”, which requires that there is no whole code word in the system that is a prefix (initial segment) of any other code word in the system. “
Concretely, let us see an example. We have the following one-to-one binary code system, represented using a dictionary.
1 | A: 00 |
We could check the word one by one to see whether the system satisfies the “prefix property”. A was coded as 00, while none of the codes of B, C, D, and E are started with 00. Using the same way, we check B, C, D, and E, and confirm that it is a prefix-free code system.
If we change the above system a little bit to the following system:
1 | A: 00 |
The new system is still one-to-one correspondence. However, it is no-longer a prefix-free code system, because the code of A 00 was shown as the prefix in the code of C which is 001.
Prefix-Free Code Tree
We represent the above prefix-free code system as a binary tree.
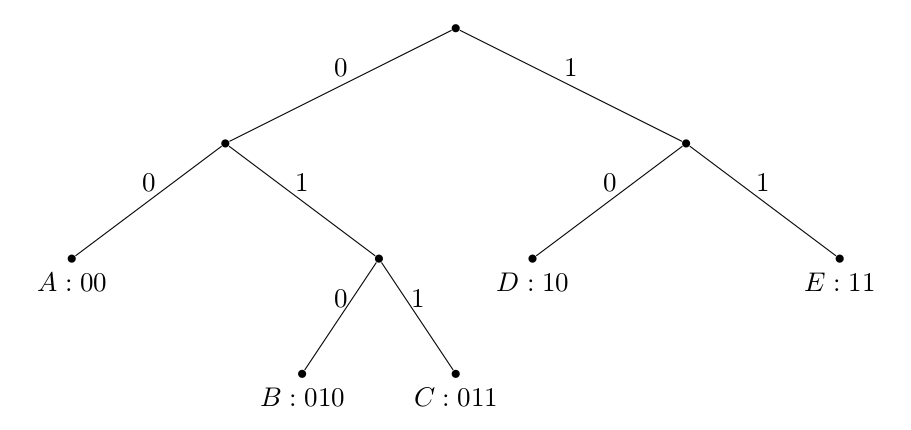
Suppose the probability of choosing the left branch is the same as choosing the right branch, i.e., $P(0) = P(1) = \frac{1}{2}$ for each node, we have: $P(A) = \frac{1}{4}$, $P(B) = \frac{1}{8}$, $P(C) = \frac{1}{8}$, $P(D) = \frac{1}{4}$, $P(E) = \frac{1}{4}$, and $P(A) + P(B) + P(C) + P(D) + P(E) = 1$.
It should be noted that $P(0) = P(1) = \frac{1}{2}$ was used just for illustration purpose, it might not be true in real examples. But even if the branching probabilities are not the same, the sum of all the leaf probabilities should always be exactly 1.
Huffman Tree
Huffman tree is a prefix-free code tree. The specialty of Huffman tree compared to an ordinary prefix-free code tree is that it minimizes the probability weighted mean of code length in the system. Here the “probability” is the probability of word shown in the system. For example, we have a system “AAAAABBBBCCCDDE”, the probabilities of words are $P(A) = \frac{1}{3}$, $P(B) = \frac{4}{15}$, $P(C) = \frac{1}{5}$, $P(D) = \frac{2}{15}$, $P(E) = \frac{1}{15}$.
The $O(n\log n)$ and $O(n)$ algorithms of constructing a Huffman tree were described in the Huffman tree Wikipedia.
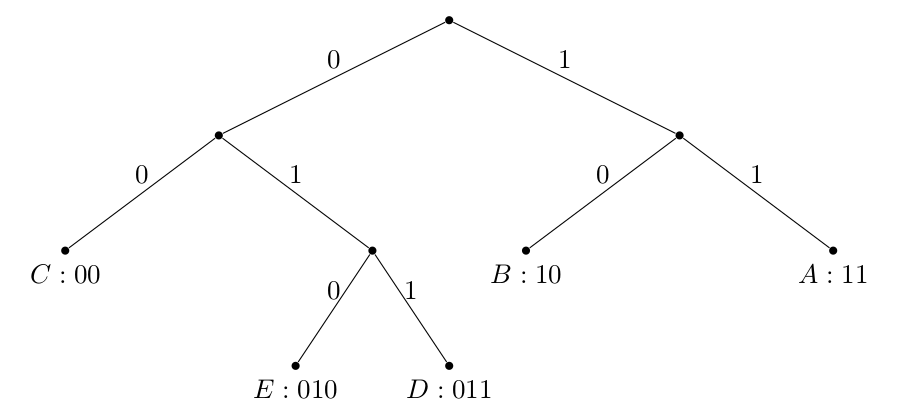
The Huffman tree of this example constructed is:
Constructing Huffman Tree
I first wanted to try implementing Huffman coding on my own, but later I found that probably does not worth spending my time. There are some open-sourced Huffman coding codes on GitHub, and there are two Python libraries of Huffman coding, huffman and dahuffman, available.
So let us try to construct the Huffman tree for the system “AAAAABBBBCCCDDE” using Huffman and dahuffman libraries.
To install huffman or dahuffman:
1 | pip install huffman |
Huffman Library
Use huffman library:
1 | import huffman |
We got the huffman coding:
1 | {'A': '11', 'B': '10', 'C': '00', 'D': '011', 'E': '010'} |
Dahuffman Library
Use dahuffman library:
1 | from dahuffman import HuffmanCodec |
We got the Huffman coding:
1 | bits code (value) symbol |
It seems that _EOF is a default symbol for Huffman coding, I currently have not found out how to get rid of _EOF for Huffman coding. However, huffman library resulted in the same Huffman coding as dahuffman library if I introduce _EOF.
Use huffman library:
1 | import huffman |
We got the huffman coding:
1 | {'A': '11', 'B': '10', 'C': '00', 'D': '011', 'E': '0101', 'EOF': '0100'} |
Which is exactly the same as the Huffman coding obtained using dahuffman library.
Conclusion
Using huffman or dahuffman library, we could easily construct a Huffman tree without knowing too many details about the tree constructing algorithms. For a more realistic example, we are going to do Huffman coding for the words in the passage:
Bellman was born in 1920 in New York City to non-practising Jewish parents of Polish and Russian descent, Pearl (née Saffian) and John James Bellman, who ran a small grocery store on Bergen Street near Prospect Park, Brooklyn. He attended Abraham Lincoln High School, Brooklyn in 1937, and studied mathematics at Brooklyn College where he earned a BA in 1941. He later earned an MA from the University of Wisconsin–Madison. During World War II he worked for a Theoretical Physics Division group in Los Alamos. In 1946 he received his Ph.D at Princeton under the supervision of Solomon Lefschetz. Beginning 1949 Bellman worked for many years at RAND corporation and it was during this time that he developed dynamic programming.
Use huffman library:
1 | import huffman |
We got the huffman coding:
1 | {'(née': '1111111', |
The more frequent the word is, the fewer bits are required to encode the word. For example, the word a was coded as 00100 (5 bits), while the word RAND was coded as 0101110 (7 bits).
Reference
Prefix-Free Code and Huffman Coding