Median-of-Medians Selection Algorithm

   blog 20 minutes read (About 2984 words)  visits

Introduction

Although the name of the median-of-medians selection algorithm suggests the algorithm finds the median of an unsorted array by finding the median of the medians from each subarray, the algorithm is actually an $O(N)$ selection algorithm for finding the $i$-th smallest element in an unsorted array by finding the approximate median of the array for partition. The median of medians from each subarray is not necessary the median of the entire array, but it is a good enough pivot for partitioning the array into two subarrays, one of which contains the $i$-th smallest element.

In this blog post, I would like to quickly discuss the median-of-medians selection algorithm, its asympotoic complexity analysis, and its implementation in C++.

Prerequisite

Master Theorem

The master theorem is useful for the asymptotic analysis for divide-and-conquer algorithms. It states that the runtime of the divide-and-conquer algorithm could usually be described as

$$
\begin{align}
T(N) &=
\begin{cases}
\Theta(1) & \text{if $N = 1$}\\
aT(\frac{N}{b}) + f(N) & \text{if $N > 1$}\\
\end{cases} \\
\end{align}
$$

where $a \geq 1$ and $b > 1$.

The master theorem states that

  1. If $f(N) = O(N^{\log_{b} a - \epsilon})$ for some constant $\epsilon > 0$, then $T(N) = \Theta(N^{\log_{b} a})$.
  2. If $f(N) = \Theta(N^{\log_{b} a})$, then $T(N) = \Theta(N^{\log_{b} a} \lg N)$.
  3. If $f(N) = \Omega(N^{\log_{b} a + \epsilon})$ for some constant $\epsilon > 0$, and if $aT(\frac{N}{b}) \leq cf(N)$ for some constant $c < 1$ and all sufficiently large N, then $T(N) = \Theta(f(N))$.

Median-of-Medians Algorithm

The median-of-medians selection algorithm solves the selection problem, i.e., finding the $i$-th smallest element in an unsorted array. The core idea is if we can find a good enough pivot and its location in the array if sorted, we can partition the array into two subarrays, one of which contains the $i$-th smallest element. We already know that given a pivot a partition algorithm can partition the array into two subarrays in $O(N)$ time. For any array of size $N$, if we can find a pivot that is approximately the median of the array, we would only have to recursively partition the array roughly $O(\log N)$ times to find the $i$-th smallest element. Of course, finding the approximate median of the array should not take more than $O(N)$ time. Otherwise, why not just sort the array and find the $i$-th smallest element in $O(N \log N)$ time?

Algorithm Analysis

To find the approximate median of an unsorted array, we can use the median-of-medians algorithm. The idea is to divide the array into subarrays of certain size $k$, sort each subarray in constant time (because the subarray size is always a constant), and find the median of each subarray. Then, we recursively find the approximate median of the medians to approximate median of the entire array. The approximate median usually has some theoretical guarantees that it is close to the median of the entire array.

For example, as illustrated in the figure below, the array can be divided into subarrays of size $k = 5$ recursively. If the entire array size is 5, we would find the approximate median of the array in the fractional range of $[p_{1}, 1-p_{1}]$ where $p_{1} = \frac{2}{5}$, which is exactly the median of the array. If the entire array size is $5^2 = 25$, we would find the approximate median of the array in the fractional range of $[p_{2}, 1-p_{2}]$ where $p_{2} = p_{1} \times \frac{3}{5} + \frac{2}{5} \times \frac{1}{5^{1}} = \frac{2}{5} \times \frac{3}{5} + \frac{2}{5} \times \frac{1}{5} = \frac{8}{25}$. If the entire array size is $5^3 = 125$, we would find the approximate median of the array in the fractional range of $[p_{3}, 1-p_{3}]$ where $p_{3} = p_{2} \times \frac{3}{5} + \frac{2}{5} \times \frac{1}{5^{2}} = \frac{8}{25} \times \frac{3}{5} + \frac{2}{5} \times \frac{1}{25} = \frac{26}{125}$. If the entire array size is $5^{i}$, we would find the approximate median of the array in the fractional range of $[p_{i}, 1-p_{i}]$ where $p_{i} = p_{i-1} \times \frac{3}{5} + \frac{2}{5} \times \frac{1}{5^{i-1}} = p_{i-1} \times \frac{3}{5} + \frac{2}{5^{i}}$.

Median-of-Medians Algorithm

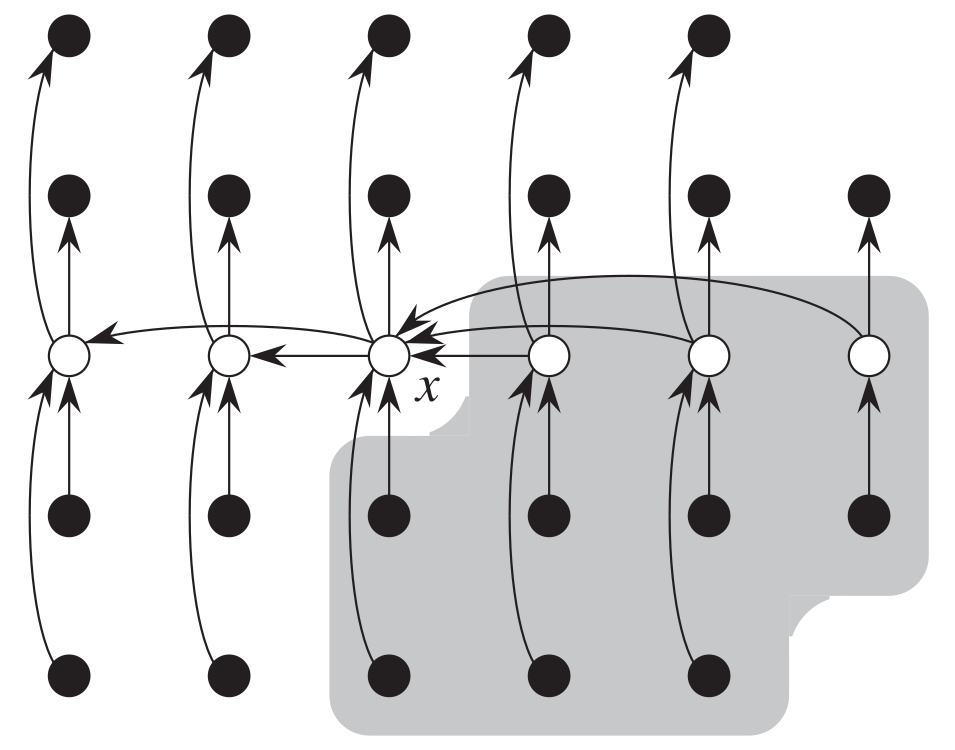
Let’s further analyze exactly the value of $p_{i}$ given $i$.

$$
\begin{align}
p_{i} &= p_{i-1} \times \frac{3}{5} + \frac{2}{5^{i}} \\
&= \left( p_{i-2} \times \frac{3}{5} + \frac{2}{5^{i-1}} \right) \times \frac{3}{5} + \frac{2}{5^{i}} \\
&= p_{i-2} \times \left( \frac{3}{5} \right)^{2} + \frac{2 + 2 \times 3}{5^{i}} \\
&= \left( p_{i-3} \times \frac{3}{5} + \frac{2}{5^{i-2}} \right) \times \left( \frac{3}{5} \right)^{2} + \frac{2 + 2 \times 3}{5^{i}} \\
&= p_{i-3} \times \left( \frac{3}{5} \right)^{3} + \frac{2 + 2 \times 3 + 2 \times 3^{2}}{5^{i}} \\
&= \cdots \\
&= p_{1} \times \left( \frac{3}{5} \right)^{i-1} + \frac{2 + 2 \times 3 + 2 \times 3^{2} + \cdots + 2 \times 3^{i-2}}{5^{i}} \\
&= \frac{2}{5} \times \left( \frac{3}{5} \right)^{i-1} + \frac{\frac{2\left(1 - 3^{i-1}\right)}{1 - 3}}{5^{i}} \\
&= \frac{2}{5} \times \left( \frac{3}{5} \right)^{i-1} + \frac{3^{i-1} - 1}{5^{i}} \\
&= \frac{2}{5} \times \left( \frac{3}{5} \right)^{i-1} + \left(\frac{3}{5}\right)^{i-1} \frac{1}{5} - \frac{1}{5^{i}} \\
&= \left(\frac{3}{5}\right)^{i} - \frac{1}{5^{i}} \\
\end{align}
$$

In general, when the array can be divided into subarrays of size $k$ recursively, we have

$$
\begin{align}
p_{i} &= p_{i-1} \times \frac{\lceil \frac{k}{2} \rceil}{k} + \frac{\lceil \frac{k}{2} \rceil - 1}{k^{i}} \\
&= \left( p_{i-2} \times \frac{\lceil \frac{k}{2} \rceil}{k} + \frac{\lceil \frac{k}{2} \rceil - 1}{k^{i-1}} \right) \times \frac{\lceil \frac{k}{2} \rceil}{k} + \frac{\lceil \frac{k}{2} \rceil - 1}{k^{i}} \\
&= p_{i-2} \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{2} + \frac{\lceil \frac{k}{2} \rceil - 1 + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil}{k^{i}} \\
&= \left( p_{i-3} \times \frac{\lceil \frac{k}{2} \rceil}{k} + \frac{\lceil \frac{k}{2} \rceil - 1}{k^{i-2}} \right) \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{2} + \frac{\lceil \frac{k}{2} \rceil - 1 + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil + \cdots + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil^{i-3}}{k^{i}} \\
&= p_{i-3} \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{3} + \frac{\lceil \frac{k}{2} \rceil - 1 + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil + \cdots + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil^{i-2}}{k^{i}} \\
&= \cdots \\
&= p_{1} \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{i-1} + \frac{\lceil \frac{k}{2} \rceil - 1 + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil + \cdots + (\lceil \frac{k}{2} \rceil - 1) \times \lceil \frac{k}{2} \rceil^{i-2}}{k^{i}} \\
&= \frac{\lceil \frac{k}{2} \rceil - 1}{k} \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{i-1} + \frac{\frac{\left( \lceil \frac{k}{2} \rceil - 1 \right)\left(1 - \lceil \frac{k}{2} \rceil^{i-1}\right)}{1 - \lceil \frac{k}{2} \rceil}}{k^{i}} \\
&= \frac{\lceil \frac{k}{2} \rceil - 1}{k} \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{i-1} + \frac{\lceil \frac{k}{2} \rceil^{i-1} - 1}{k^{i}} \\
&= \frac{\lceil \frac{k}{2} \rceil - 1}{k} \times \left( \frac{\lceil \frac{k}{2} \rceil}{k} \right)^{i-1} + \left(\frac{\lceil \frac{k}{2} \rceil}{k}\right)^{i-1} \frac{1}{k} - \frac{1}{k^{i}} \\
&= \left(\frac{\lceil \frac{k}{2} \rceil}{k}\right)^{i} - \frac{1}{k^{i}} \\
\end{align}
$$

We could see that when $i$ is large, i.e., when the array size $N$ is large because $i = \lceil \log_{k}{N} \rceil$, $p_{i}$ is very small and the approximate of the median of the array can be extremely poor in the worst case.

This suggests that using the median-of-medians algorithm to find the approximate median of the array might not be a good idea when the array size is large.

Nevertheless, the recursive divide-and-conquer median-of-medians algorithm can be analyzed using the master theorem to show that the algorithm is $O(N)$.

In our case,

$$
\begin{align}
T(N) &=
\begin{cases}
\Theta(1) & \text{if $N \leq k$}\\
k T(\frac{N}{k}) + \Theta(1) & \text{if $N > k$}\\
\end{cases} \\
\end{align}
$$

Because $T(N) = aT(\frac{N}{b}) + f(N)$, $a = k$, $b = k$, $\log_{b} {a} = 1$, $\epsilon = k$, $f(N) = O(N^{\log_{b} {a} - \epsilon})$, the master theorem tells us that $T(N) = \Theta(N^{\log_{b} {a}}) = \Theta(N)$ for the median-of-medians algorithm.

Algorithm Implementation

The median-of-medians algorithm can be implemented in C++ as follows.

approximate_median.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <algorithm>
#include <array>
#include <iostream>
#include <iterator>
#include <vector>

// Find the approximate median value.
template <typename T, size_t SmallArraySize, class ForwardIt>
T median_of_medians(ForwardIt first, ForwardIt last)
{
    auto const size{std::distance(first, last)};
    if (size <= SmallArraySize)
    {
        std::array<T, SmallArraySize> v;
        std::copy(first, last, std::begin(v));
        std::sort(std::begin(v), std::begin(v) + size);
        size_t const median_index{static_cast<size_t>(size / 2)};
        return v.at(median_index);
    }
    std::vector<T> medians;
    for (auto it{first}; it < last; it += SmallArraySize)
    {
        auto const sub_last{std::min(it + SmallArraySize, last)};
        medians.push_back(median_of_medians<T, SmallArraySize>(it, sub_last));
    }
    return median_of_medians<T, SmallArraySize>(medians.begin(), medians.end());
}

// Find the median value using sorting.
template <typename T, class ForwardIt>
T median_using_sorting(ForwardIt first, ForwardIt last)
{
    auto const size{std::distance(first, last)};
    std::vector<T> v;
    v.reserve(size);
    std::copy(first, last, std::back_inserter(v));
    std::sort(v.begin(), v.end());
    size_t const median_index{static_cast<size_t>(size / 2)};
    return v.at(median_index);
}

int main()
{
    constexpr size_t SmallArraySize{5};
    std::vector<int> const v{0,   55,  66,  77,  11,  22,  33,  44,  88,  99,
                             100, 101, 102, 103, 104, 105, 106, 107, 108, 109};
    std::cout << "Original Vector:" << std::endl;
    std::copy(std::begin(v), std::end(v),
              std::ostream_iterator<int>(std::cout, " "));
    std::cout << std::endl;
    auto const median{median_using_sorting<int>(std::begin(v), std::end(v))};
    std::cout << "Median Using Sorting: " << median << std::endl;
    auto const approximate_median{
        median_of_medians<int, SmallArraySize>(std::begin(v), std::end(v))};
    std::cout << "Approximate Median Using Median of Medians Algorithm: "
              << approximate_median << std::endl;
}

From the test result below, we can see that the approximate median of the array using the median-of-medians algorithm is 102, which is close to the median of the array using sorting, which is 100.

1
2
3
4
5
6
$ g++ approximate_median.cpp -o approximate_median --std=c++14
$ ./approximate_median
Original Vector:
0 55 66 77 11 22 33 44 88 99 100 101 102 103 104 105 106 107 108 109
Median Using Sorting: 100
Approximate Median Using Median of Medians Algorithm: 102

Median-of-Medians Selection Algorithm

The median-of-medians selection algorithm is a selection algorithm that combines the $O(N)$ partition algorithm and the $O(N)$ median-of-medians algorithm to find the $i$-th smallest element in an unsorted array. Concretely, we find the approximate median of the array using the median-of-medians algorithm, using the approximate median as the pivot to partition the array into two subarrays and we would know how many elements are there in the left and right subarrays after partition. If the number of elements in the left subarray is less than $i$, we would recursively find the $i$-th smallest element in the right subarray. If the number of elements in the left subarray is greater than $i$, we would recursively find the $i$-th smallest element in the left subarray. If the number of elements in the left subarray is equal to $i$, we would return the pivot as the $i$-th smallest element.

Algorithm Analysis

We will analyze the median-of-medians selection algorithm in the worst case. In the worst case, the approximate median that’s found using the median-of-medians algorithm will always be at the boundary of the fractional range and the $i$-th smallest element would never occur until all the elements in the entire array are excluded from the partition. This means that each time we partition the array, we only exclude the theoretical lower-bound number of elements from the entire array for finding the median.

Based on the analysis of the median-of-medians algorithm, given an array of size $N$, we know that the median-of-medians algorithm is $O(N)$ and the maximum number of remained elements after exclusion using partition is $N(1-p)$ where $p = \left(\frac{\lceil \frac{k}{2} \rceil}{k}\right)^{i} - \frac{1}{k^{i}}$ in $(0, 1)$ and $i = \lceil \log_{k}{N} \rceil$.

So to find the most difficult $i$-th smallest element in the worst case, we have

$$
\begin{align}
N(1 - p_{1})(1 - p_{2})\cdots(1 - p_{i})\cdots(1 - p_{n}) & = 1
\end{align}
$$

We need to know how many iterations $n$ we have to run the median-of-medians selection algorithm to find the $i$-th smallest element in the worst case. It is, however, difficult to solve the equation and compute the exact value for $n$ because $p_{i}$ is a function of $k$ and $N$ and this $N$ is subject to change in each iteration.

We can, however, make a bold assumption that $p_{i}$ is a constant $p$ where $p \leq p_{i}$ for any $i$ and solve the equation to find the value for $n$. Such $p$ can just be $p = \left(\frac{\lceil \frac{k}{2} \rceil}{k}\right)^{\lceil \log_{k}{N} \rceil} - \frac{1}{k^{\lceil \log_{k}{N} \rceil}}$ in $(0, 1)$.

Therefore, the number of iterations we have run the median-of-medians selection algorithm to find the $i$-th smallest element in the worst case can be easily solved using the following equation.

$$
\begin{align}
N(1 - p)^{n} & = 1 \\
\end{align}
$$

The asymptotic complexity of the median-of-medians selection algorithm can be computed as follows.

$$
\begin{align}
T(N) &= \sum_{i=1}^{n} \left( \underbrace{O\left(N (1 - p)^{i-1}\right)}_{\text{median of medians}} + \underbrace{O\left(N (1 - p)^{i-1}\right)}_{\text{partition}} \right) \\
&= \sum_{i=1}^{n} O\left(N (1 - p)^{i-1}\right) \\
&= O\left(N \sum_{i=1}^{n} (1 - p)^{i-1}\right) \\
&= O\left(N \frac{1 \left( 1- (1-p)^{n} \right)}{1 - \left(1 - p\right)} \right) \\
&= O\left(N \frac{1 - (1-p)^{n}}{p} \right) \\
&= O\left(\frac{N - N(1-p)^{n}}{p} \right) \\
&= O\left(\frac{N - 1}{p} \right) \\
&= O(N) \\
\end{align}
$$

Therefore, even if we have assumed everything in the worst scenario, the median-of-medians selection algorithm is still $O(N)$. It is also important to note that the asymptotic constant for the median-of-medians selection algorithm can be very large as you could probably feel from the analysis.

Algorithm Implementation

The median-of-medians selection algorithm can be implemented in C++ as follows.

selection.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <algorithm>
#include <array>
#include <iostream>
#include <iterator>
#include <vector>

// Find the approximate median value.
template <typename T, size_t SmallArraySize, class ForwardIt>
T median_of_medians(ForwardIt first, ForwardIt last)
{
    auto const size{std::distance(first, last)};
    if (size <= SmallArraySize)
    {
        std::array<T, SmallArraySize> v;
        std::copy(first, last, std::begin(v));
        std::sort(std::begin(v), std::begin(v) + size);
        size_t const median_index{static_cast<size_t>(size / 2)};
        return v.at(median_index);
    }
    std::vector<T> medians;
    for (auto it{first}; it < last; it += SmallArraySize)
    {
        auto const sub_last{std::min(it + SmallArraySize, last)};
        medians.push_back(median_of_medians<T, SmallArraySize>(it, sub_last));
    }
    return median_of_medians<T, SmallArraySize>(medians.begin(), medians.end());
}

template <typename T, class ForwardIt>
T custom_selection_algorithm(ForwardIt first, ForwardIt last, size_t i)
{
    auto const size{std::distance(first, last)};
    // Check if the size is large or equal to the order statistics index.
    if (size < i)
    {
        throw std::out_of_range{"The order statistics is out of range."};
    }
    // Find the approximate median value.
    auto const pivot{median_of_medians<T, 5>(first, last)};
    // Partition the elements around the pivot.
    auto const partition_it{
        std::partition(first, last, [pivot](T const n) { return n < pivot; })};
    // Calculate the number of elements less than the pivot.
    auto const num_less_than_pivot{std::distance(first, partition_it)};
    // Check if the pivot is the order statistics.
    if (num_less_than_pivot == i)
    {
        return pivot;
    }
    // Check if the pivot is less than the order statistics.
    else if (num_less_than_pivot < i)
    {
        return custom_selection_algorithm<T>(partition_it, last,
                                             i - num_less_than_pivot);
    }
    // Check if the pivot is greater than the order statistics.
    else
    {
        return custom_selection_algorithm<T>(first, partition_it, i);
    }
}

template <typename T, class ForwardIt>
T custom_selection(ForwardIt first, ForwardIt last, size_t i)
{
    // Copy the elements to a vector.
    std::vector<T> v;
    v.reserve(std::distance(first, last));
    std::copy(first, last, std::back_inserter(v));
    // Call the custom selection algorithm.
    return custom_selection_algorithm<T>(v.begin(), v.end(), i);
}

template <typename T, class ForwardIt>
T sorting_selection(ForwardIt first, ForwardIt last, size_t i)
{
    auto const size{std::distance(first, last)};
    if (size < i)
    {
        throw std::out_of_range{"The order statistics is out of range."};
    }
    std::vector<T> v;
    v.reserve(size);
    std::copy(first, last, std::back_inserter(v));
    std::sort(v.begin(), v.end());
    return v.at(i);
}

int main()
{
    std::vector<int> const v{0,   55,  66,  77,  11,  22,  33,  44,  88,  99,
                             100, 101, 102, 103, 104, 105, 106, 107, 108, 109};
    std::cout << "Vector:" << std::endl;
    std::copy(std::begin(v), std::end(v),
              std::ostream_iterator<int>(std::cout, " "));
    std::cout << std::endl;
    auto const order_statistics_index{v.size() / 2};

    auto const median_of_medians_selection_result{custom_selection<int>(
        std::begin(v), std::end(v), order_statistics_index)};
    std::cout << "Selection of " << order_statistics_index
              << "-th Smallest Value"
              << " Using Median of Medians Selection Algorithm: "
              << median_of_medians_selection_result << std::endl;
    auto const sorting_selection_result{sorting_selection<int>(
        std::begin(v), std::end(v), order_statistics_index)};
    std::cout << "Selection of " << order_statistics_index
              << "-th Smallest Value"
              << " Using Sorting Selection Algorithm: "
              << sorting_selection_result << std::endl;
}

From the test result below, we can see that the $i$-th smallest element in the array using the median-of-medians selection algorithm is 100, which is exactly the same as the $i$-th smallest element in the array using the sorting selection algorithm.

1
2
3
4
5
6
$ g++ selection.cpp -o selection --std=c++14
$ ./selection
Vector:
0 55 66 77 11 22 33 44 88 99 100 101 102 103 104 105 106 107 108 109
Selection of 10-th Smallest Value Using Median of Medians Selection Algorithm: 100
Selection of 10-th Smallest Value Using Sorting Selection Algorithm: 100

Conclusions

The median-of-medians selection algorithm is an $O(N)$ selection algorithm for finding the $i$-th smallest element in an unsorted array. However, its asymptotic constant can be very large and the performance of the algorithm implementation can be less satistactory in practice.

References

Median-of-Medians Selection Algorithm

https://leimao.github.io/blog/Median-of-Medians-Select-Algorithm/

Author

Lei Mao

Posted on

02-18-2024

Updated on

02-18-2024

Licensed under

 

Like this article? Support the author with

Comments

  Follow   Sponsor

Advertisement


×