Introduction to YOLOs
Introduction
YOLO (You Only Look Once) is one of the popular fast object detection algorithms. Here I will talk about some details that people who had not actually implemented the model, including myself, would have thought about. Those details are usually described superficially in the paper and the posts from other bloggers will hardly talk about.
YOLO v1
Conceptually, YOLO v1 divided the square image input to $S \times S$ grids. The prediction tensor has size of $S \times S \times (B \times 5 + C)$.
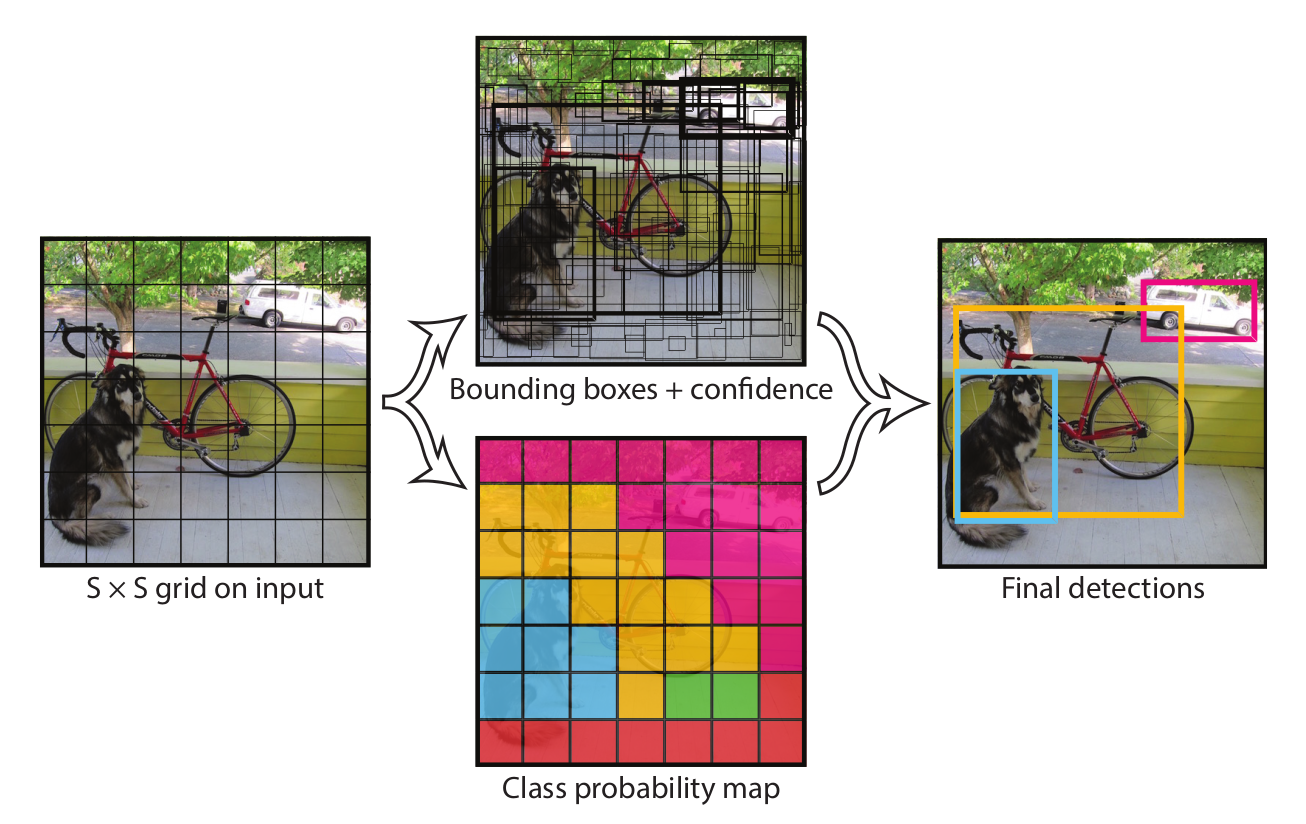
$B$ is the number of bounding boxes for one grid cell. $C$ is the number of candidate classes for one grid cell. The classification is conducted on grid cells only, instead of bounding boxes. It should also be noted that there is no “anchor box” used in YOLO v1. The bounding box representation is $x$, $y$, $w$, $h$, $\text{conf}$, totally 5 elements. $x$ and $y$ are scaled to relative coordinates with a scale of [0, 1] inside the grid. $w$ and $h$ are scaled to [0, 1] against the width and height of the image input. There is a very good illustration of how to convert those coordinates in this blog post.
The confidence score $\text{conf}$ is a little bit obscure. The paper described it as $\text{Pr(object)} \times \mathrm{IOU_{truth}^{pred}}$.
$$
\text{Pr(object)} =
\begin{cases}
1 & \text{if the center of the object is considered inside the box} \\
0 & \text{otherwise}
\end{cases}
$$
The object will only be assigned once to one bounding box.
To better understand it, you may first ignore its actual meaning, and just think it as a scalar value to be predicted.
Now that we know YOLO is a neural network that takes an image of fixed size and outputs some values of the shape described above. During training, what are the ground truth values for those predicted values? What’s different from calculating these ground truth values in YOLO v1 to some latest object detection models is that the ground truth values in YOLO v1 are calculated on the flight after predictions are being made. This sounds awkward because in machine learning usually the training data is pre-processed so that the inputs and ground truth values will be available before the actual training. Let us see what is happening in YOLO.
For each grid, we have to predicted $(B \times 5 + C)$ values, including {$x_1$, $x_2$, $\cdots$, $x_B$}, {$y_1$, $y_2$, $\cdots$, $y_B$}, {$w_1$, $w_2$, $\cdots$, $w_B$}, {$h_1$, $h_2$, $\cdots$, $h_B$}, {$\mathrm{conf_{1}}$, $\mathrm{conf_{2}}$, $\cdots$, $\mathrm{conf_{B}}$}, and {$c_1$, $c_2$, $\cdots$, $c_C$}. If there is an ground-truth bounding box {$x_{\text{gt}}, y_{\text{gt}}, w_{\text{gt}}, h_{\text{gt}}$} whose center is located inside the grid, then the IOUs of the ground-truth box with all the bounding boxes from this grid will be calculated, {$\mathrm{IOU_{1}}, \mathrm{IOU_{2}}, \cdots, \mathrm{IOU_{B}}$},. Among all these bounding boxes, the only one, say bounding box $i$, who has the largest IOU was considered to contain an object ($\text{Pr(object)} = 1$), and got {$x_{\text{gt}}, y_{\text{gt}}, w_{\text{gt}}, h_{\text{gt}}, \mathrm{IOU_{i}}$} as ground-truth values for {$x_i, y_i, w_i, h_i, \mathrm{conf_{i}}$}. The ground-truth for the rest of the bounding boxes does not matter because they will not be taken into account in the loss function.
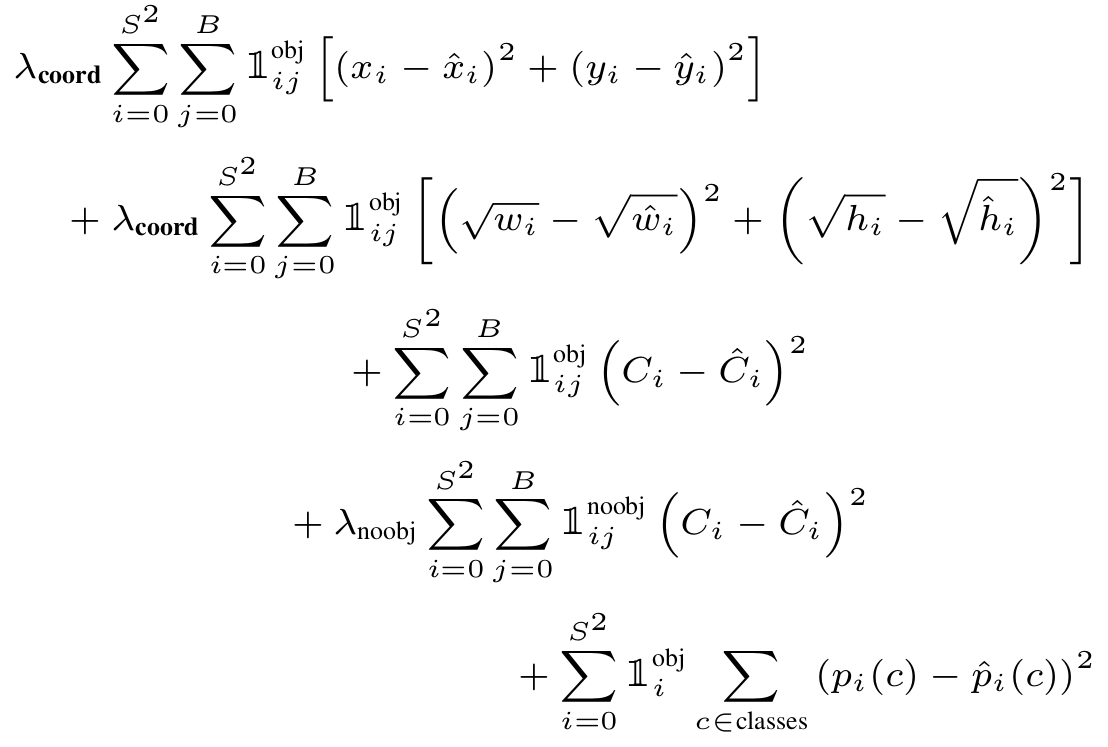
What if one bounding box has the highest IOU with multiple ground-truth bounding boxes, which is very likely in practice? This could be arbitrary. One way is to randomly choose anyone.
What is there are more than $B$ objects whose center is located inside one grid cell? This is not likely in practice because data preprocessing could filter those images.
How about the ground-truth value of class probabilities {$c_1$, $c_2$, $\cdots$, $c_C$}? If there is no object in the grid cell, it does not matter because they will not be taken into account in the loss function. If there is only one object of class $j$ in the grid cell, just set $c_j = 1$ and the rest of $c$ values to be 0. If there are more than one objects, say $m$ objects of classes {$j_1$, $j_2$, $\cdots$, $j_m$}, in the grid cell, just set $c_{j_1} = \frac{1}{m}$, $c_{j_2} = \frac{1}{m}$, $\cdots$, $c_{j_m} = \frac{1}{m}$ and the rest of $c$ values to be 0.
YOLO v2
YOLO v2 first did some unsupervised clustering on bounding box coordinates, they found the the centroid of some clusters of bounding boxes that could be used for object detection training. These boxes are called prior boxes or anchor boxes. Say we have 5 centroids from the bounding box clustering, {$x_1$, $y_1$, $w_1$, $h_1$}, {$x_2$, $y_2$, $w_2$, $h_2$}, {$x_3$, $y_3$, $w_3$, $h_3$}, {$x_4$, $y_4$, $w_4$, $h_4$}, {$x_5$, $y_5$, $w_5$, $h_5$}, where $x$, $y$ are scaled relative to grid cell to a range of [0, 1], $w$, and $h$ are scaled relative to image input to a range of [0, 1]. These 5 centroids are served as the anchor boxes for each grid cell. Unlike anchor boxes in SSD, these anchor box does not necessarily have their center at the center of grid cell.
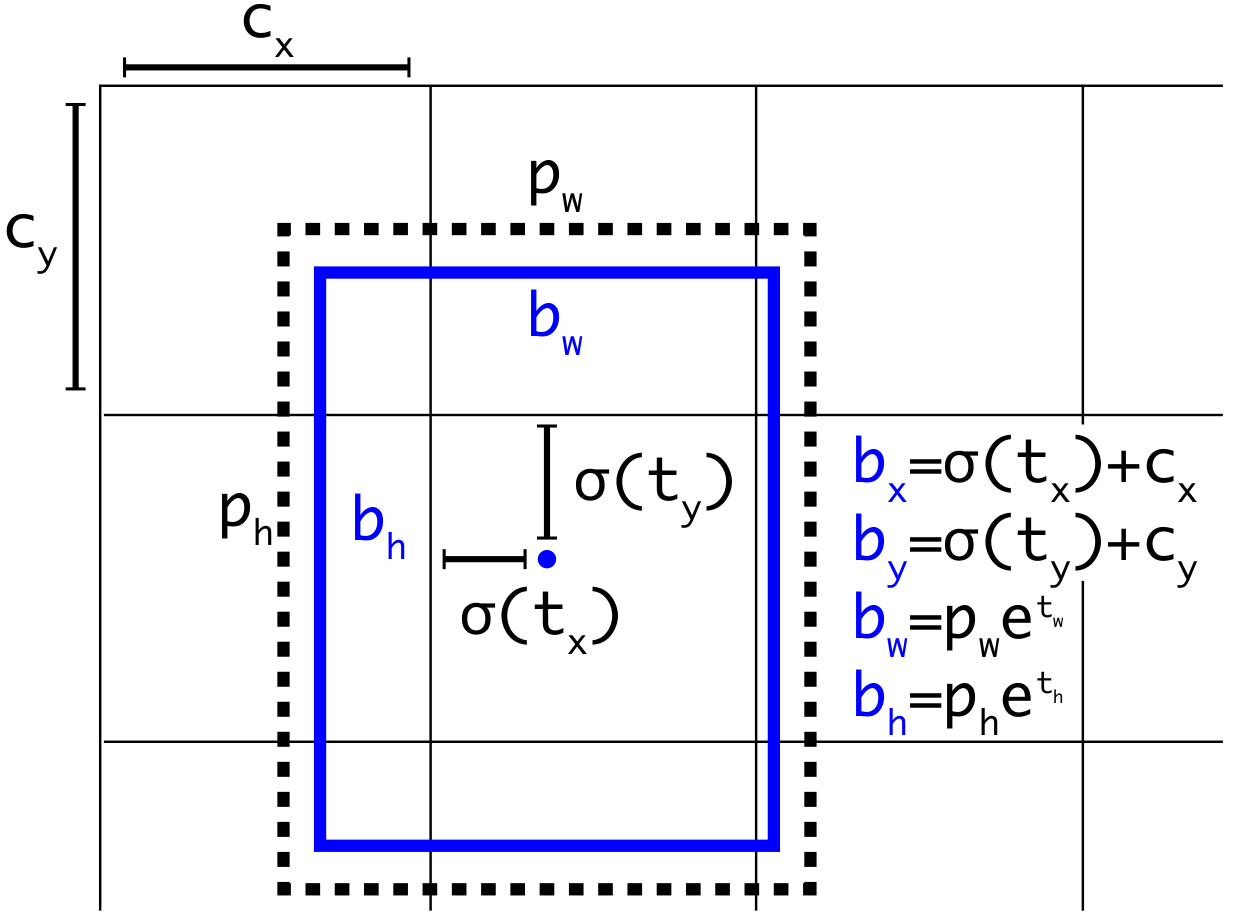
The prediction tensor from YOLO v2 has size of $S \times S \times B \times (5 + C)$. $B$ now becomes the number of anchor boxes / bounding boxes for one grid cell (each anchor box predicts one bounding box). Unlike YOLO v1, YOLO v2 does classification for each bounding box. The 5 box parameters are slightly different in YOLO v2 since it started to use anchor boxes. YOLO v2 is also trying to predict offsets of predicted box to anchor box, but in a slightly different way. The predicted bounding box has 5 coordinates {$t_x$, $t_y$, $t_w$, $t_h$, $t_o$}. Its relationship to anchor box {$c_x$, $c_y$, $c_w$, $c_h$} is as follows.
$$
b_x = \sigma(t_x) + c_x\\
b_y = \sigma(t_y) + c_y\\
b_w = p_w e^{t_w}\\
b_h = p_h e^{t_h}\\
\text{Pr(object)} \times \mathrm{IOU_{truth}^{pred}} = \sigma(t_o)\\
$$
Where $b_x$, $b_y$ are the center coordinates of bounding box scaled relative to image input to a range of [0, 1], and $b_w$, $b_n$ are scaled the width and height of bounding box relative to image input to a range of [0, 1]. $c_x$ and $c_y$ are the scaled offsets of the left corner of the grid cell to the left corner of the image in a range of [0, 1]. It should be noted that only the width and height information of the anchor boxes were used above. $\sigma$ is the sigmoid function, although it looked weired in the above settings. The definition of $\text{Pr(object)}$ is the same as the one in YOLO v1.
There is not too much difference to the YOLO v1 bounding box regression. You still have to calculate $\text{Pr(object)}$ and $\mathrm{IOU_{truth}^{pred}}$ on the flight during training. In my opinion, although the author used the concept of anchor box, the anchor box in YOLO v2 is merely increasing the number of candidate boxes and all the target values could not be pre-computed before training. Personally, I would not consider those “anchor boxes” real anchor boxes.
YOLO v2 also talked about how to put object classification and object detection together to train object detection networks. We have a lot of data, such as ImageNet to do object classification. Those data have labels and usually have more classes than the number of classes in the object detection dataset such as COCO. The author thinks of a way to merge the two datasets together so that the trained neural network could do object detection for the object classes from both the object detection and classification datasets.
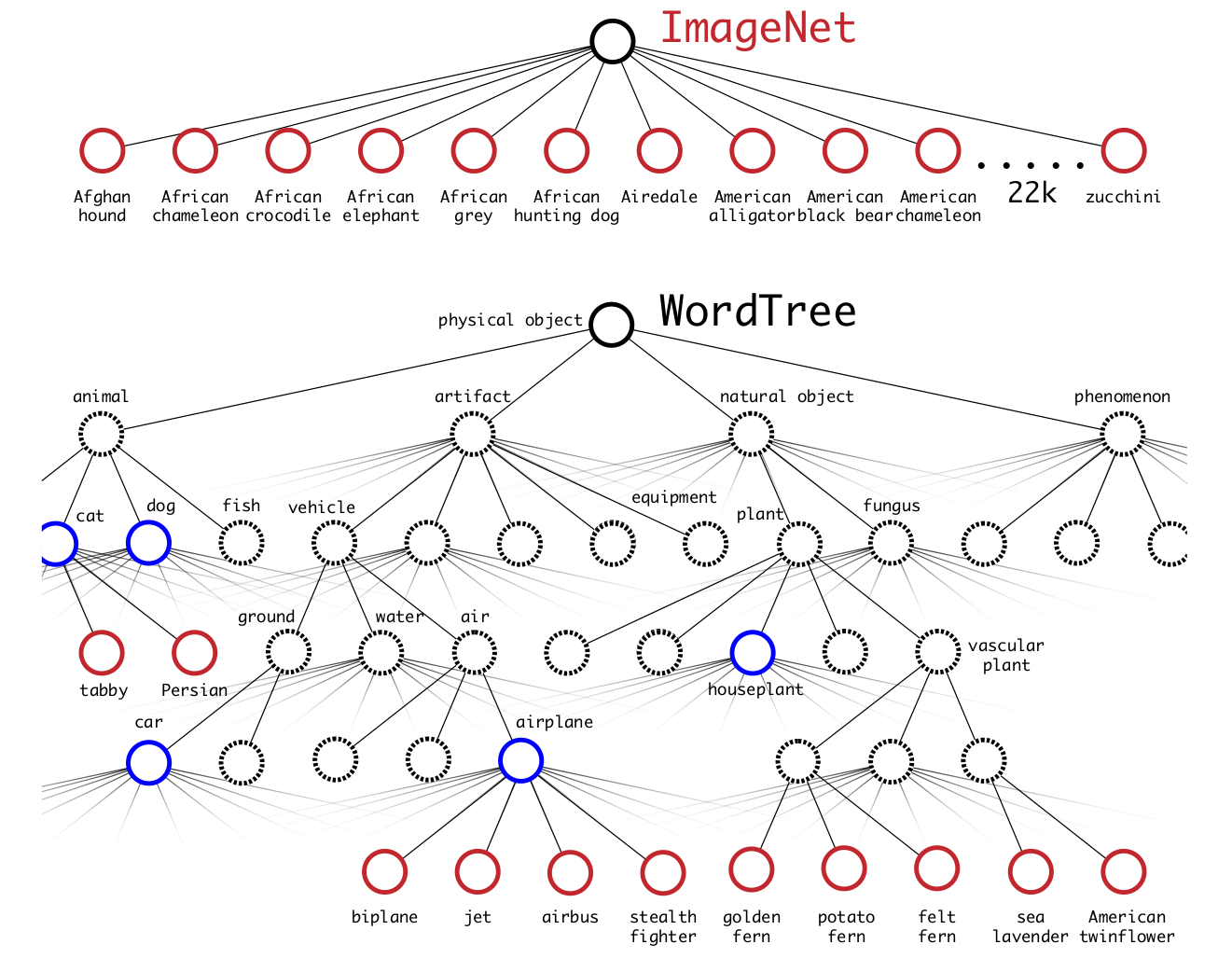
Basically, they “relabel” the images from the two datasets to “hierarchical labels” using WordTree structure, and they use hierarchical architecture to train using the “hierarchical labels”. Check out hierarchical models and Softmax at one of my course projects presentations at TTIC. I will probably talk about hierarchical models in the future on my personal website as well. During training, when the model sees a detection image, the back propagation is the same as usual. When the model sees a classification image the back propagation was only conducted for the classification loss, i.e., the regression loss is muted. This is like a dessert but should not be considered seriously in my opinion.
YOLO v3
To be continued.
References
Introduction to YOLOs