CUDA Matrix Multiplication Optimization

   article 2 hours read (About 19282 words)  visits

Introduction

General matrix multiplication (GEMM) is a fundamental operation in linear algebra. It is also a very important operation in many scientific computing applications, such as machine learning and deep learning.

In this article, we will discuss how to optimize the performance of FP32 GEMM on NVIDIA GPUs using CUDA and how to extend the FP32 GEMM optimizations to FP16 GEMM using NVIDIA Tensor Cores.

General Matrix Multiplication

GEMM operation computes $D = AB + C$, where $D \in \mathbb{R}^{m \times n}$, $A \in \mathbb{R}^{m \times k}$, $B \in \mathbb{R}^{k \times n}$, $C \in \mathbb{R}^{m \times n}$. In computer programs, usually $A$ and $B$ are constant input matrices and $C$ will be overwritten by the output matrix $D$.

In our implementations, we assume all the matrices, $A$, $B$, $C$ and $D$, are stored in the row-major order on memory with the leading dimension padded to 64 bytes for FP32 matrices and 32 bytes for FP16 matrices.

Naive Implementation with Non-Coalesced Memory Access

The naive implementation is to use 2D blocks, where each thread is responsible for computing one element of the output matrix. Concretely, for each thread with global thread index $(t_m, t_n)$, where $t_m \in [1, m]$ and $t_n \in [1, n]$, it computes $D_{t_m, t_n} = \sum_{t_k=1}^{k} A_{t_m, t_k} B_{t_k, t_n} + C_{t_m, t_n}$.

The following code snippet shows the naive implementation.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
template <typename T>
__global__ void gemm_v00(size_t m, size_t n, size_t k, T alpha, T const* A,
                         size_t lda, T const* B, size_t ldb, T beta, T* C,
                         size_t ldc)
{
    // Compute the row and column of C that this thread is responsible for.
    size_t const C_row_idx{blockIdx.x * blockDim.x + threadIdx.x};
    size_t const C_col_idx{blockIdx.y * blockDim.y + threadIdx.y};

    // Each thread compute
    // C[C_row_idx, C_col_idx] = alpha * A[C_row_idx, :] * B[:, C_col_idx] +
    // beta * C[C_row_idx, C_col_idx].
    if (C_row_idx < m && C_col_idx < n)
    {
        T sum{static_cast<T>(0)};
        for (size_t k_idx{0U}; k_idx < k; ++k_idx)
        {
            sum += A[C_row_idx * lda + k_idx] * B[k_idx * ldb + C_col_idx];
        }
        C[C_row_idx * ldc + C_col_idx] =
            alpha * sum + beta * C[C_row_idx * ldc + C_col_idx];
    }
}

template <typename T>
void launch_gemm_kernel_v00(size_t m, size_t n, size_t k, T const* alpha,
                            T const* A, size_t lda, T const* B, size_t ldb,
                            T const* beta, T* C, size_t ldc,
                            cudaStream_t stream)
{
    dim3 const block_dim{32U, 32U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(m) + block_dim.x - 1U) / block_dim.x,
        (static_cast<unsigned int>(n) + block_dim.y - 1U) / block_dim.y, 1U};
    gemm_v00<T><<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B,
                                                     ldb, *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

In addition to other drawbacks from the naive algorithm, however, there is a major problem with this implementation, which is the non-coalesced memory access for both reading and writing the global memory. In our implementation specifically, because of the oversight that the fast thread index is used for indexing the row of $A$ and $C$, the threads in the same warp read the elements from the same column of $A$ that is stored in row-major order on memory, resulting in a non-coalesced memory access as the reads are completely non-consecutive. The same problem also happens when the warp overwrites the elements of $C$. The threads in the same warp read the same element of $B$, resulting in a broadcast memory access which is not affected by the oversight.

The performance of this FP32 GEMM implementation is only 0.27 TFLOPS on an NVIDIA GeForce RTX 3090 GPU, which is very poor.

Naive Implementation with Coalesced Memory Access

The fix to the non-coalesced memory access is to use the fast thread index for indexing the row of matrices that are stored in row-major order on memory instead so that the threads in the same warp read or overwrite the elements from the same row of the matrices are coalesced. In our implementation, we just need to swap the fast thread index and the slow thread index in the kernel function.

The following code snippet shows the naive implementation with coalesced memory access.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
template <typename T>
__global__ void gemm_v01(size_t m, size_t n, size_t k, T alpha, T const* A,
                         size_t lda, T const* B, size_t ldb, T beta, T* C,
                         size_t ldc)
{
    // Compute the row and column of C that this thread is responsible for.
    size_t const C_col_idx{blockIdx.x * blockDim.x + threadIdx.x};
    size_t const C_row_idx{blockIdx.y * blockDim.y + threadIdx.y};

    // Each thread compute
    // C[C_row_idx, C_col_idx] = alpha * A[C_row_idx, :] * B[:, C_col_idx] +
    // beta * C[C_row_idx, C_col_idx].
    if (C_row_idx < m && C_col_idx < n)
    {
        T sum{static_cast<T>(0)};
        for (size_t k_idx{0U}; k_idx < k; ++k_idx)
        {
            sum += A[C_row_idx * lda + k_idx] * B[k_idx * ldb + C_col_idx];
        }
        C[C_row_idx * ldc + C_col_idx] =
            alpha * sum + beta * C[C_row_idx * ldc + C_col_idx];
    }
}

template <typename T>
void launch_gemm_kernel_v01(size_t m, size_t n, size_t k, T const* alpha,
                            T const* A, size_t lda, T const* B, size_t ldb,
                            T const* beta, T* C, size_t ldc,
                            cudaStream_t stream)
{
    dim3 const block_dim{32U, 32U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + block_dim.x - 1U) / block_dim.x,
        (static_cast<unsigned int>(m) + block_dim.y - 1U) / block_dim.y, 1U};
    gemm_v01<T><<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B,
                                                     ldb, *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

Now, because of the fix, the threads in the same warp read the elements from the same row of $B$ that is stored in row-major order on memory, resulting in a coalesced memory access. The same thing also happens when the warp overwrites the elements of $C$. The threads in the same warp read the same element of $A$, resulting in a broadcast memory access. Therefore, this implementation should perform much better than the one with non-coalesced memory access.

The performance of this FP32 GEMM implementation becomes 1.72 TFLOPS on an NVIDIA GeForce RTX 3090 GPU, which is much better than the previous implementation. However, considering the theoretical peak performance of the GPU is 35.58 TFLOPS, the performance of this implementation is still very poor.

Implementation with 2D Block Tiling

Because the previous implementation accesses the global memory frequently, the GEMM implementation becomes memory-bound. Because accessing the shared memory is much faster than accessing the global memory, to improve the performance, we can use the shared memory to cache the input matrices $A$ and $B$ for data reuse.

However, because the shared memory size is limited, we cannot cache the entire input matrices $A$ and $B$ in the shared memory. Instead, we can cache a 2D tile of $A$ and $B$ in the shared memory and use the 2D tile to compute a 2D tile of the output matrix $D$. Then, we can load the next 2D tile of $A$ and $B$ to the shared memory and compute the next 2D tile of $D$.

Mathematically, given a GEMM operation $D = AB + C$, where $D \in \mathbb{R}^{m \times n}$, $A \in \mathbb{R}^{m \times k}$, $B \in \mathbb{R}^{k \times n}$, $C \in \mathbb{R}^{m \times n}$, the matrices could be divided into smaller matrices.

$$
A =
\begin{bmatrix}
A_{1,1}^{d_{bm} \times d_{bk}} & A_{1,2}^{d_{bm} \times d_{bk}} & \cdots & A_{1,k/d_{bk}}^{d_{bm} \times d_{bk}} \\
A_{2,1}^{d_{bm} \times d_{bk}} & A_{2,2}^{d_{bm} \times d_{bk}} & \cdots & A_{2,k/d_{bk}}^{d_{bm} \times d_{bk}} \\
\vdots & \vdots & \ddots & \vdots \\
A_{m/d_{bm},1}^{d_{bm} \times d_{bk}} & A_{m/d_{bm},2}^{d_{bm} \times d_{bk}} & \cdots & A_{m/d_{bm},k/d_{bk}}^{d_{bm} \times d_{bk}} \\
\end{bmatrix}
$$

$$
B =
\begin{bmatrix}
B_{1,1}^{d_{bk} \times d_{bn}} & B_{1,2}^{d_{bk} \times d_{bn}} & \cdots & B_{1,n/d_{bn}}^{d_{bk} \times d_{bn}} \\
B_{2,1}^{d_{bk} \times d_{bn}} & B_{2,2}^{d_{bk} \times d_{bn}} & \cdots & B_{2,n/d_{bn}}^{d_{bk} \times d_{bn}} \\
\vdots & \vdots & \ddots & \vdots \\
B_{k/d_{bk},1}^{d_{bk} \times d_{bn}} & B_{k/d_{bk},2}^{d_{bk} \times d_{bn}} & \cdots & B_{k/d_{bk},n/d_{bn}}^{d_{bk} \times d_{bn}} \\
\end{bmatrix}
$$

$$
C =
\begin{bmatrix}
C_{1,1}^{d_{bm} \times d_{bn}} & C_{1,2}^{d_{bm} \times d_{bn}} & \cdots & C_{1,n/d_{bn}}^{d_{bm} \times d_{bn}} \\
C_{2,1}^{d_{bm} \times d_{bn}} & C_{2,2}^{d_{bm} \times d_{bn}} & \cdots & C_{2,n/d_{bn}}^{d_{bm} \times d_{bn}} \\
\vdots & \vdots & \ddots & \vdots \\
C_{m/d_{bm},1}^{d_{bm} \times d_{bn}} & C_{m/d_{bm},2}^{d_{bm} \times d_{bn}} & \cdots & C_{m/d_{bm},n/d_{bn}}^{d_{bm} \times d_{bn}} \\
\end{bmatrix}
$$

$$
D =
\begin{bmatrix}
D_{1,1}^{d_{bm} \times d_{bn}} & D_{1,2}^{d_{bm} \times d_{bn}} & \cdots & D_{1,n/d_{bn}}^{d_{bm} \times d_{bn}} \\
D_{2,1}^{d_{bm} \times d_{bn}} & D_{2,2}^{d_{bm} \times d_{bn}} & \cdots & D_{2,n/d_{bn}}^{d_{bm} \times d_{bn}} \\
\vdots & \vdots & \ddots & \vdots \\
D_{m/d_{bm},1}^{d_{bm} \times d_{bn}} & D_{m/d_{bm},2}^{d_{bm} \times d_{bn}} & \cdots & D_{m/d_{bm},n/d_{bn}}^{d_{bm} \times d_{bn}} \\
\end{bmatrix}
$$

Each small matrix in $D$ is computed as multiple small matrix multiplications and accumulations.

$$
D_{b_m,b_n}^{d_{bm} \times d_{bn}} = \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}}
$$

In this implementation, each 2D block with block index $(b_m, b_n)$, where $b_m \in [1, m/d_{bm}]$ and $b_n \in [1, n/d_{bn}]$, is responsible for computing one small matrix $D_{b_m,b_n}^{d_{bm} \times d_{bn}}$. The shared memory is used to cache a 2D tile of $A$ and $B$ with size $d_{bm} \times d_{bk}$ and $d_{bk} \times d_{bn}$, respectively. The 2D tile of $A$ is indexed by $(b_m, b_k)$, where $b_m \in [1, m/d_{bm}]$ and $b_k \in [1, k/d_{bk}]$. The 2D tile of $B$ is indexed by $(b_k, b_n)$, where $b_k \in [1, k/d_{bk}]$ and $b_n \in [1, n/d_{bn}]$. The cache and small matrix multiplication compute process is repeated for $k/d_{bk}$ times until the entire small matrix $D_{b_m,b_n}^{d_{bm} \times d_{bn}}$ is accumulated.

Similar to the previous implementations, each block requires $d_{bm} \times d_{bn}$ threads to compute the small matrix $D_{b_m, b_n}^{d_{bm} \times d_{bn}}$ and each thread with block thread index $(t_m, t_n)$, where $t_m \in [1, d_{bm}]$ and $t_n \in [1, d_{bn}]$, is responsible for computing one element of the small matrix.

$$
\begin{aligned}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{t_m,t_n}
&= \left( \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m,t_n} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_m,t_n} + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m,t_n} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{t_k=1}^{d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{t_m,t_k} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m,t_n} \\
\end{aligned}
$$

The following code snippet shows the implementation with 2D block tiling.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t NUM_THREADS, size_t BLOCK_TILE_SKEW_SIZE_X = 0U, size_t BLOCK_TILE_SKEW_SIZE_K = 0U>
__device__ void load_data_to_shared_memory(T const* A, size_t lda,
                                           T const* B, size_t ldb,
                                           T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K + BLOCK_TILE_SKEW_SIZE_K],
                                           T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X],
                                           size_t thread_block_tile_idx,
                                           size_t thread_linear_idx,
                                           size_t m, size_t n,
                                           size_t k)
{
    // Load data from A on DRAM to A_thread_block_tile on shared memory.
#pragma unroll
    for (size_t load_idx{0U};
         load_idx <
         (BLOCK_TILE_SIZE_Y * BLOCK_TILE_SIZE_K + NUM_THREADS - 1U) /
             NUM_THREADS;
         ++load_idx)
    {
        size_t const A_thread_block_tile_row_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) /
            BLOCK_TILE_SIZE_K};
        size_t const A_thread_block_tile_col_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) %
            BLOCK_TILE_SIZE_K};
        size_t const A_row_idx{blockIdx.y * BLOCK_TILE_SIZE_Y +
                               A_thread_block_tile_row_idx};
        size_t const A_col_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
                               A_thread_block_tile_col_idx};

        // These boundary checks might slow down the kernel to some extent.
        // But they guarantee the correctness of the kernel for all
        // different GEMM configurations.
        T val{static_cast<T>(0)};
        if (A_row_idx < m && A_col_idx < k)
        {
            val = A[A_row_idx * lda + A_col_idx];
        }
        // This if will slow down the kernel.
        // Add static asserts from the host code to guarantee this if is
        // always true.
        static_assert(BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS ==
                      0U);
        // if (A_thread_block_tile_row_idx < BLOCK_TILE_SIZE_Y &&
        //     A_thread_block_tile_col_idx < BLOCK_TILE_SIZE_K)
        // {
        //     A_thread_block_tile[A_thread_block_tile_row_idx]
        //                        [A_thread_block_tile_col_idx] = val;
        // }
        A_thread_block_tile[A_thread_block_tile_row_idx]
                           [A_thread_block_tile_col_idx] = val;
    }
// Load data from B on DRAM to B_thread_block_tile on shared memory.
#pragma unroll
    for (size_t load_idx{0U};
         load_idx <
         (BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_X + NUM_THREADS - 1U) /
             NUM_THREADS;
         ++load_idx)
    {
        size_t const B_thread_block_tile_row_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) /
            BLOCK_TILE_SIZE_X};
        size_t const B_thread_block_tile_col_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) %
            BLOCK_TILE_SIZE_X};
        size_t const B_row_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
                               B_thread_block_tile_row_idx};
        size_t const B_col_idx{blockIdx.x * BLOCK_TILE_SIZE_X +
                               B_thread_block_tile_col_idx};

        // These boundary checks might slow down the kernel to some extent.
        // But they guarantee the correctness of the kernel for all
        // different GEMM configurations.
        T val{static_cast<T>(0)};
        if (B_row_idx < k && B_col_idx < n)
        {
            val = B[B_row_idx * ldb + B_col_idx];
        }
        // This if will slow down the kernel.
        // Add static asserts from the host code to guarantee this if is
        // always true.
        static_assert(BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS ==
                      0U);
        // if (B_thread_block_tile_row_idx < BLOCK_TILE_SIZE_K &&
        //     B_thread_block_tile_col_idx < BLOCK_TILE_SIZE_X)
        // {
        //     B_thread_block_tile[B_thread_block_tile_row_idx]
        //                        [B_thread_block_tile_col_idx] = val;
        // }
        B_thread_block_tile[B_thread_block_tile_row_idx]
                           [B_thread_block_tile_col_idx] = val;
    }
}

template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K>
__global__ void gemm_v02(size_t m, size_t n, size_t k, T alpha, T const* A,
                         size_t lda, T const* B, size_t ldb, T beta, T* C,
                         size_t ldc)
{
    // Avoid using blockDim.x * blockDim.y as the number of threads per block.
    // Because it is a runtime constant and the compiler cannot optimize the
    // loop unrolling based on that.
    // Use a compile time constant instead.
    constexpr size_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y};
    size_t const thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};

    // Compute the row and column of C that this thread is responsible for.
    size_t const C_col_idx{blockIdx.x * blockDim.x + threadIdx.x};
    size_t const C_row_idx{blockIdx.y * blockDim.y + threadIdx.y};

    // Cache a tile of A and B in shared memory for data reuse.
    __shared__ T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K];
    __shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];

    size_t const num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
                                        BLOCK_TILE_SIZE_K};

    T sum{static_cast<T>(0)};
    for (size_t thread_block_tile_idx{0U};
         thread_block_tile_idx < num_thread_block_tiles;
         ++thread_block_tile_idx)
    {
        load_data_to_shared_memory<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
                                   BLOCK_TILE_SIZE_K, NUM_THREADS>(
            A, lda, B, ldb, A_thread_block_tile, B_thread_block_tile,
            thread_block_tile_idx, thread_linear_idx, m, n, k);
        __syncthreads();

#pragma unroll
        for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
        {
            // Doing this results in 2 TOPS.
            // Suppose blockDim.x = blockDim.y = 32.
            // Effectively, for a warp, in one iteration, we read the value from
            // A_thread_block_tile at the same location on the shared memory
            // resulting in a broadcast, we also read 32 values that have no
            // bank conflicts from B_thread_block_tile. Even with that, all the
            // values have to be read from the shared memory and consequence is
            // the shared memory instruction runs very intensively just to
            // compute a small number of values using simple arithmetic
            // instructions, which is not efficient.
            sum += A_thread_block_tile[threadIdx.y][k_i] *
                   B_thread_block_tile[k_i][threadIdx.x];
        }
        __syncthreads();
    }
    if (C_row_idx < m && C_col_idx < n)
    {
        C[C_row_idx * ldc + C_col_idx] =
            alpha * sum + beta * C[C_row_idx * ldc + C_col_idx];
    }
}

template <typename T>
void launch_gemm_kernel_v02(size_t m, size_t n, size_t k, T const* alpha,
                            T const* A, size_t lda, T const* B, size_t ldb,
                            T const* beta, T* C, size_t ldc,
                            cudaStream_t stream)
{
    // Feel free to play with the block tile sizes.
    // The algorithm correctness should always be guaranteed.
    constexpr unsigned int BLOCK_TILE_SIZE_X{32U};
    constexpr unsigned int BLOCK_TILE_SIZE_Y{32U};
    constexpr unsigned int BLOCK_TILE_SIZE_K{32U};
    constexpr unsigned int NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y};
    static_assert(BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS == 0U);
    static_assert(BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS == 0U);
    dim3 const block_dim{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + block_dim.x - 1U) / block_dim.x,
        (static_cast<unsigned int>(m) + block_dim.y - 1U) / block_dim.y, 1U};
    gemm_v02<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K>
        <<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
                                              *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

The performance of this FP32 GEMM implementation becomes 2.66 TFLOPS on an NVIDIA GeForce RTX 3090 GPU, which is much better than the previous implementation. However, it is still far from the theoretical peak performance of the GPU.

The problem of this implementation is that the shared memory is accessed very frequently. Even if accessing the shared memory is much faster than accessing the global memory, the shared memory instruction runs very intensively just to compute a small number of values using simple arithmetic instructions, which is not efficient. Therefore, the performance of this implementation is still limited by the memory bandwidth, this time from the shared memory.

Implementation with 2D Block Tiling and 1D Thread Tiling

To further improve the performance, we can alleviate the shared memory bandwidth problem by further caching some even smaller tiles of the input matrices $A$ and $B$ from the shared memory to the registers of the threads. This time, each thread is responsible for computing a small tile of the output matrix $D$ instead of one single element. Because the registers are the fastest to access, the performance of this implementation should be much better than the previous one.

We start with only caching the data of matrix $B$ from the shared memory to the registers. Each thread with block thread index $(t_m, t_n)$, where $t_m \in [1, d_{bm} / d_{tm}]$ and $t_n \in [1, d_{bn}]$, is now responsible for computing $d_{tm}$ elements of the small matrix, where $d_{tm}$ is the thread tile size.

$$
\begin{aligned}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{t_m : t_m + d_{tm},t_n}
&= \left( \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n} + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{t_k=1}^{d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{t_m : t_m + d_{tm},t_k} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n} \\
\end{aligned}
$$

In our previous implementation without thread tiling, to compute one element of the small matrix, we need to read $d_{bk}$ values from the cached matrix $A$ in the shared memory and $d_{bk}$ values from the cached matrix $B$ in the shared memory. In total, we need to read $2d_{k}$ values from the shared memory.

Now, with 1D thread tiling, to compute $d_{tm}$ elements of the small matrix, we only need to read $d_{bk} \times d_{tm}$ values from the cached matrix $A$ in the shared memory and $d_{bk}$ values from the cached matrix $B$ in the shared memory. Specifically, in each inner loop, $\left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n}$ is cached in the register to be reused for $d_{tm}$ times. In total, we need to read $d_{bk} \times d_{tm} + d_{bk}$ values from the shared memory. On average, to compute one element of the small matrix, we need to read $d_{bk} + d_{bk} / d_{tm}$ values from the shared memory.

Because $d_{bk} + d_{bk} / d_{tm} < 2d_{k}$, the shared memory is accessed less frequently and the shared memory bandwidth problem is alleviated.

The following code snippet shows the implementation with 2D block tiling and 1D thread tiling.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t THREAD_TILE_SIZE_Y>
__global__ void gemm_v03(size_t m, size_t n, size_t k, T alpha, T const* A,
                         size_t lda, T const* B, size_t ldb, T beta, T* C,
                         size_t ldc)
{
    // Avoid using blockDim.x * blockDim.y as the number of threads per block.
    // Because it is a runtime constant and the compiler cannot optimize the
    // loop unrolling based on that.
    // Use a compile time constant instead.
    constexpr size_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
                                 THREAD_TILE_SIZE_Y};
    size_t const thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};

    // Cache a tile of A and B in shared memory for data reuse.
    __shared__ T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K];
    __shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];

    size_t const num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
                                        BLOCK_TILE_SIZE_K};

    // Each thread in the block processes BLOCK_TILE_SIZE_Y output values.
    // Specifically, these values corresponds to
    // C[blockIdx.y * BLOCK_TILE_SIZE_Y + threadIdx.x / BLOCK_TILE_SIZE_X *
    // THREAD_TILE_SIZE_Y : blockIdx.y * BLOCK_TILE_SIZE_Y + (threadIdx.x /
    // BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_Y][blockIdx.x *
    // BLOCK_TILE_SIZE_X + threadIdx.x % BLOCK_TILE_SIZE_X]
    T C_thread_results[THREAD_TILE_SIZE_Y] = {static_cast<T>(0)};

    for (size_t thread_block_tile_idx{0U};
         thread_block_tile_idx < num_thread_block_tiles;
         ++thread_block_tile_idx)
    {
        load_data_to_shared_memory<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
                                   BLOCK_TILE_SIZE_K, NUM_THREADS>(
            A, lda, B, ldb, A_thread_block_tile, B_thread_block_tile,
            thread_block_tile_idx, thread_linear_idx, m, n, k);
        __syncthreads();

#pragma unroll
        for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
        {
            size_t const B_thread_block_tile_row_idx{k_i};
            // B_val is cached in the register to alleviate the pressure on the
            // shared memory access.
            T const B_val{
                B_thread_block_tile[B_thread_block_tile_row_idx]
                                   [thread_linear_idx % BLOCK_TILE_SIZE_X]};
#pragma unroll
            for (size_t thread_tile_row_idx{0U};
                 thread_tile_row_idx < THREAD_TILE_SIZE_Y;
                 ++thread_tile_row_idx)
            {
                size_t const A_thread_block_tile_row_idx{
                    thread_linear_idx / BLOCK_TILE_SIZE_X * THREAD_TILE_SIZE_Y +
                    thread_tile_row_idx};
                size_t const A_thread_block_tile_col_idx{k_i};
                T const A_val{A_thread_block_tile[A_thread_block_tile_row_idx]
                                                 [A_thread_block_tile_col_idx]};
                C_thread_results[thread_tile_row_idx] += A_val * B_val;
            }
        }
        __syncthreads();
    }

// Write the results to DRAM.
#pragma unroll
    for (size_t thread_tile_row_idx{0U};
         thread_tile_row_idx < THREAD_TILE_SIZE_Y; ++thread_tile_row_idx)
    {
        size_t const C_row_idx{blockIdx.y * BLOCK_TILE_SIZE_Y +
                               thread_linear_idx / BLOCK_TILE_SIZE_X *
                                   THREAD_TILE_SIZE_Y +
                               thread_tile_row_idx};
        size_t const C_col_idx{blockIdx.x * BLOCK_TILE_SIZE_X +
                               thread_linear_idx % BLOCK_TILE_SIZE_X};
        if (C_row_idx < m && C_col_idx < n)
        {
            C[C_row_idx * ldc + C_col_idx] =
                alpha * C_thread_results[thread_tile_row_idx] +
                beta * C[C_row_idx * ldc + C_col_idx];
        }
    }
}

template <typename T>
void launch_gemm_kernel_v03(size_t m, size_t n, size_t k, T const* alpha,
                            T const* A, size_t lda, T const* B, size_t ldb,
                            T const* beta, T* C, size_t ldc,
                            cudaStream_t stream)
{
    // Feel free to play with the block tile sizes.
    // The algorithm correctness should always be guaranteed.
    constexpr unsigned int BLOCK_TILE_SIZE_X{64U};
    constexpr unsigned int BLOCK_TILE_SIZE_Y{64U};
    constexpr unsigned int BLOCK_TILE_SIZE_K{8U};
    // Each thread computes THREAD_TILE_SIZE_Y values of C.
    constexpr unsigned int THREAD_TILE_SIZE_Y{8U};
    constexpr unsigned int NUM_THREADS_PER_BLOCK{
        BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y / THREAD_TILE_SIZE_Y};
    static_assert(BLOCK_TILE_SIZE_Y % THREAD_TILE_SIZE_Y == 0U);
    static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_K == 0U);
    static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_X == 0U);
    dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + BLOCK_TILE_SIZE_X - 1U) /
            BLOCK_TILE_SIZE_X,
        (static_cast<unsigned int>(m) + BLOCK_TILE_SIZE_Y - 1U) /
            BLOCK_TILE_SIZE_Y,
        1U};
    gemm_v03<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
             THREAD_TILE_SIZE_Y><<<grid_dim, block_dim, 0U, stream>>>(
        m, n, k, *alpha, A, lda, B, ldb, *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

The performance of this FP32 GEMM implementation becomes 8.91 TFLOPS on an NVIDIA GeForce RTX 3090 GPU. It seems that we have been making good progress.

Implementation with 2D Block Tiling and 2D Thread Tiling

If the number of registers is not a bottleneck for the performance, we can further improve the performance by caching the data of both matrix $A$ and $B$ from the shared memory to the registers. Each thread with block thread index $(t_m, t_n)$, where $t_m \in [1, d_{bm} / d_{tm}]$ and $t_n \in [1, d_{bn} / d_{tn}]$, is now responsible for computing $d_{tm} \times d_{tn}$ elements of the small matrix, where $d_{tm}$ and $d_{tn}$ are the thread tile sizes for the row and column, respectively.

$$
\begin{aligned}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{t_m : t_m + d_{tm},t_n : t_n + d_{tn}}
&= \left( \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n : t_n + d_{tn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n : t_n + d_{tn}} + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n : t_n + d_{tn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{t_k=1}^{d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{t_m : t_m + d_{tm},t_k} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n : t_n + d_{tn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m : t_m + d_{tm},t_n : t_n + d_{tn}} \\
\end{aligned}
$$

In our previous implementation with 1D thread tiling, to compute one element of the small matrix, we need to read $d_{bk} + d_{bk} / d_{tm}$ values from the shared memory on average.

Now, with 2D thread tiling, to compute $d_{tm} \times d_{tn}$ elements of the small matrix, we only need to read $d_{bk} \times (d_{tm} + d_{tn})$ values from the shared memory. Specifically, in each inner loop, $\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{t_m : t_m + d_{tm},t_k}$ and $\left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n : t_n + d_{tn}}$ are cached in the register to be reused for computing the matrix multiplication $\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{t_m : t_m + d_{tm},t_k} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n : t_n + d_{tn}}$. In total, we need to read $d_{bk} \times (d_{tm} + d_{tn})$ values from the shared memory. On average, to compute one element of the small matrix, we need to read $d_{bk} / d_{tm} + d_{bk} / d_{tn}$ values from the shared memory.

Because $d_{bk} / d_{tm} + d_{bk} / d_{tn} < d_{bk} + d_{bk} / d_{tm}$, the shared memory is accessed even less frequently and the shared memory bandwidth problem is further alleviated.

There is an alternative way to describe the 2D thread tiling implementation.

Mathematically, given a matrix multiplication and accumulation operation $D_{b_m,b_n}^{d_{bm} \times d_{bn}} = \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}}$, where $D_{b_m,b_n} \in \mathbb{R}^{d_{bm} \times d_{bn}}$, $A_{b_m,b_k} \in \mathbb{R}^{d_{bm} \times d_{bk}}$, $B_{b_k,b_n} \in \mathbb{R}^{d_{bk} \times d_{bn}}$, $C_{b_m,b_n} \in \mathbb{R}^{d_{bm} \times d_{bn}}$, the matrices could be divided into smaller matrices.

$$
A_{b_m,b_k}^{d_{bm} \times d_{bk}} =
\begin{bmatrix}
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,1}^{d_{tm} \times d_{tk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,2}^{d_{tm} \times d_{tk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,d_{bk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,1}^{d_{tm} \times d_{tk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,2}^{d_{tm} \times d_{tk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,d_{bk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{tm},1}^{d_{tm} \times d_{tk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{tm},2}^{d_{tm} \times d_{tk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{tm},d_{bk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\end{bmatrix}
$$

$$
B_{b_k,b_n}^{d_{bk} \times d_{bn}} =
\begin{bmatrix}
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,1}^{d_{tk} \times d_{tn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,2}^{d_{tk} \times d_{tn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,d_{bn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,1}^{d_{tk} \times d_{tn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,2}^{d_{tk} \times d_{tn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,d_{bn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{tk},1}^{d_{tk} \times d_{tn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{tk},2}^{d_{tk} \times d_{tn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{tk},d_{bn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\end{bmatrix}
$$

$$
C_{b_m,b_n}^{d_{bm} \times d_{bn}} =
\begin{bmatrix}
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,1}^{d_{tm} \times d_{tn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,2}^{d_{tm} \times d_{tn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,d_{bn}/d_{tn}}^{d_{tm} \times d_{tn}} \\
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,1}^{d_{tm} \times d_{tn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,2}^{d_{tm} \times d_{tn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,d_{bn}/d_{tn}}^{d_{tm} \times d_{tn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{tm},1}^{d_{tm} \times d_{tn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{tm},2}^{d_{tm} \times d_{tn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{tm},d_{bn}/d_{tn}}^{d_{tm} \times d_{tn}} \\
\end{bmatrix}
$$

$$
D_{b_m,b_n}^{d_{bm} \times d_{bn}} =
\begin{bmatrix}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,1}^{d_{tm} \times d_{tn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,2}^{d_{tm} \times d_{tn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,d_{bn}/d_{tn}}^{d_{tm} \times d_{tn}} \\
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,1}^{d_{tm} \times d_{tn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,2}^{d_{tm} \times d_{tn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,d_{bn}/d_{tn}}^{d_{tm} \times d_{tn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{tm},1}^{d_{tm} \times d_{tn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{tm},2}^{d_{tm} \times d_{tn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{tm},d_{bn}/d_{tn}}^{d_{tm} \times d_{tn}} \\
\end{bmatrix}
$$

Each small matrix in $D_{b_m,b_n}^{d_{bm} \times d_{bn}}$ is computed as multiple small matrix multiplications and accumulations.

$$
\begin{aligned}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{t_m,t_n}^{d_{tm} \times d_{tn}}
&= \left( \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m,t_n}^{d_{tm} \times d_{tn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_m,t_n}^{d_{tm} \times d_{tn}} + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m,t_n}^{d_{tm} \times d_{tn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{t_k=1}^{d_{bk} / d_{tk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{t_m,t_k}^{d_{tm} \times d_{tk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{t_k,t_n}^{d_{tk} \times d_{tn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{t_m,t_n}^{d_{tm} \times d_{tn}} \\
\end{aligned}
$$

Each thread with block thread index $(t_m, t_n)$, where $t_m \in [1, d_{bm} / d_{tm}]$ and $t_n \in [1, d_{bn} / d_{tn}]$, in the block with block index $(b_m, b_n)$, where $b_m \in [1, m/d_{bm}]$ and $b_n \in [1, n/d_{bn}]$, is responsible for computing one small matrix multiplication and accumulation $\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{t_m,t_n}^{d_{tm} \times d_{tn}}$.

In the case of 1D thread tiling described in this article, we have $d_{tm} > 1$, $d_{tk} = 1$ and $d_{tn} = 1$. In the case of 2D thread tiling in this article, we have $d_{tm} > 1$, $d_{tk} = 1$ and $d_{tn} > 1$. It is also technically feasible to do thread tiling with $d_{tk} > 1$. In the case of no thread tiling, which is actually a special case of the thread tiling, we have $d_{tm} = 1$, $d_{tk} = 1$ and $d_{tn} = 1$.

The following code snippet shows the implementation with 2D block tiling and 2D thread tiling.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
// GEMM kernel v04.
// Coalesced read and write from global memory.
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t THREAD_TILE_SIZE_X,
          size_t THREAD_TILE_SIZE_Y>
__global__ void gemm_v04(size_t m, size_t n, size_t k, T alpha, T const* A,
                         size_t lda, T const* B, size_t ldb, T beta, T* C,
                         size_t ldc)
{
    // Avoid using blockDim.x * blockDim.y as the number of threads per block.
    // Because it is a runtime constant and the compiler cannot optimize the
    // loop unrolling based on that.
    // Use a compile time constant instead.
    constexpr size_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
                                 (THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
    size_t const thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};

    // Cache a tile of A and B in shared memory for data reuse.
    __shared__ T A_thread_block_tile[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_K];
    __shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];

    size_t const num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
                                        BLOCK_TILE_SIZE_K};

    // Each thread in the block processes BLOCK_TILE_SIZE_Y output values.
    // Specifically, these values corresponds to
    // C[blockIdx.y * BLOCK_TILE_SIZE_Y + threadIdx.x / BLOCK_TILE_SIZE_X *
    // THREAD_TILE_SIZE_Y : blockIdx.y * BLOCK_TILE_SIZE_Y + (threadIdx.x /
    // BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_Y][blockIdx.x *
    // BLOCK_TILE_SIZE_X + threadIdx.x % BLOCK_TILE_SIZE_X *
    // THREAD_TILE_SIZE_X : blockIdx.x * BLOCK_TILE_SIZE_X + (threadIdx.x %
    // BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_X]
    T C_thread_results[THREAD_TILE_SIZE_Y][THREAD_TILE_SIZE_X] = {
        static_cast<T>(0)};
    // A_vals is cached in the register.
    T A_vals[THREAD_TILE_SIZE_Y] = {static_cast<T>(0)};
    // B_vals is cached in the register.
    T B_vals[THREAD_TILE_SIZE_X] = {static_cast<T>(0)};

    for (size_t thread_block_tile_idx{0U};
         thread_block_tile_idx < num_thread_block_tiles;
         ++thread_block_tile_idx)
    {

        load_data_to_shared_memory<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
                                   BLOCK_TILE_SIZE_K, NUM_THREADS>(
            A, lda, B, ldb, A_thread_block_tile, B_thread_block_tile,
            thread_block_tile_idx, thread_linear_idx, m, n, k);
        __syncthreads();

#pragma unroll
        for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
        {
            size_t const A_thread_block_tile_row_idx{
                thread_linear_idx / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                THREAD_TILE_SIZE_Y};
            size_t const A_thread_block_tile_col_idx{k_i};

#pragma unroll
            for (size_t thread_tile_row_idx{0U};
                 thread_tile_row_idx < THREAD_TILE_SIZE_Y;
                 ++thread_tile_row_idx)
            {
                // There will be shared memory bank conflicts accessing the
                // values from A_thread_block_tile. We can do it better by
                // transposing the A_thread_block_tile when we load the data
                // from DRAM.
                A_vals[thread_tile_row_idx] =
                    A_thread_block_tile[A_thread_block_tile_row_idx +
                                        thread_tile_row_idx]
                                       [A_thread_block_tile_col_idx];
            }

            size_t const B_thread_block_tile_row_idx{k_i};
            size_t const B_thread_block_tile_col_idx{
                thread_linear_idx % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                THREAD_TILE_SIZE_X};
#pragma unroll
            for (size_t thread_tile_col_idx{0U};
                 thread_tile_col_idx < THREAD_TILE_SIZE_X;
                 ++thread_tile_col_idx)
            {
                B_vals[thread_tile_col_idx] =
                    B_thread_block_tile[B_thread_block_tile_row_idx]
                                       [B_thread_block_tile_col_idx +
                                        thread_tile_col_idx];
            }

            for (size_t thread_tile_row_idx{0U};
                 thread_tile_row_idx < THREAD_TILE_SIZE_Y;
                 ++thread_tile_row_idx)
            {
                for (size_t thread_tile_col_idx{0U};
                     thread_tile_col_idx < THREAD_TILE_SIZE_X;
                     ++thread_tile_col_idx)
                {
                    C_thread_results[thread_tile_row_idx]
                                    [thread_tile_col_idx] +=
                        A_vals[thread_tile_row_idx] *
                        B_vals[thread_tile_col_idx];
                }
            }
        }
        __syncthreads();
    }

    // Write the results to DRAM.
    for (size_t thread_tile_row_idx{0U};
         thread_tile_row_idx < THREAD_TILE_SIZE_Y; ++thread_tile_row_idx)
    {
        for (size_t thread_tile_col_idx{0U};
             thread_tile_col_idx < THREAD_TILE_SIZE_X; ++thread_tile_col_idx)
        {
            size_t const C_row_idx{
                blockIdx.y * BLOCK_TILE_SIZE_Y +
                threadIdx.x / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                    THREAD_TILE_SIZE_Y +
                thread_tile_row_idx};
            size_t const C_col_idx{
                blockIdx.x * BLOCK_TILE_SIZE_X +
                threadIdx.x % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                    THREAD_TILE_SIZE_X +
                thread_tile_col_idx};
            if (C_row_idx < m && C_col_idx < n)
            {
                C[C_row_idx * ldc + C_col_idx] =
                    alpha * C_thread_results[thread_tile_row_idx]
                                            [thread_tile_col_idx] +
                    beta * C[C_row_idx * ldc + C_col_idx];
            }
        }
    }
}

template <typename T>
void launch_gemm_kernel_v04(size_t m, size_t n, size_t k, T const* alpha,
                            T const* A, size_t lda, T const* B, size_t ldb,
                            T const* beta, T* C, size_t ldc,
                            cudaStream_t stream)
{
    // Feel free to play with the block tile sizes.
    // The algorithm correctness should always be guaranteed.
    constexpr unsigned int BLOCK_TILE_SIZE_X{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_Y{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_K{16U};
    // Each thread computes THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y values of C.
    constexpr unsigned int THREAD_TILE_SIZE_X{8U};
    constexpr unsigned int THREAD_TILE_SIZE_Y{8U};
    constexpr unsigned int NUM_THREADS_PER_BLOCK{
        BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
        (THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
    static_assert(BLOCK_TILE_SIZE_X % THREAD_TILE_SIZE_X == 0U);
    static_assert(BLOCK_TILE_SIZE_Y % THREAD_TILE_SIZE_Y == 0U);
    static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_K == 0U);
    static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_X == 0U);
    static_assert(
        BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS_PER_BLOCK == 0U);
    static_assert(
        BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS_PER_BLOCK == 0U);
    dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + BLOCK_TILE_SIZE_X - 1U) /
            BLOCK_TILE_SIZE_X,
        (static_cast<unsigned int>(m) + BLOCK_TILE_SIZE_Y - 1U) /
            BLOCK_TILE_SIZE_Y,
        1U};
    gemm_v04<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
             THREAD_TILE_SIZE_X, THREAD_TILE_SIZE_Y>
        <<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
                                              *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

The performance of this FP32 GEMM implementation becomes 13.02 TFLOPS on an NVIDIA GeForce RTX 3090 GPU.

Implementation with 2D Block Tiling and 2D Thread Tiling and Vectorized Memory Access

In my previous article “CUDA Vectorized Memory Access”, I showed how to use vectorized memory access to improve the performance of a trivial memory copy kernel. Vectorized memory access reduces the number of memory transactions and therefore improves the memory bandwidth utilization. The same trick can be applied to this GEMM kernel to accelerate the data loading from global memory to the shared memory and the data loading from the shared memory to the registers.

In the previous implementation, to compute matrix multiplication, each thread would have to read a column of matrix $A$ and a row of matrix $B$ from the shared memory and cache them in the registers. Because reading the data from a column of matrix $A$ would prevent vectorized memory access, we would like to transpose the matrix $A$ when loading the data from global memory to the shared memory, so that each thread can access a row of transposed matrix $A$ and a row of matrix $B$ from the shared memory in a vectorized fashion and cache them in the registers.

The following code snippet shows the implementation with 2D block tiling and 2D thread tiling and vectorized memory access.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t NUM_THREADS, size_t BLOCK_TILE_SKEW_SIZE_X = 0U, size_t BLOCK_TILE_SKEW_SIZE_Y = 0U, typename VECTOR_TYPE = int4>
__device__ void load_data_to_shared_memory_transposed_vectorized(T const* A, size_t lda,
                                           T const* B, size_t ldb,
                                           T A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_Y + BLOCK_TILE_SKEW_SIZE_Y],
                                           T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X],
                                           size_t thread_block_tile_idx,
                                           size_t thread_linear_idx,
                                           size_t m, size_t n,
                                           size_t k)
{
    constexpr size_t NUM_VECTOR_UNITS{sizeof(VECTOR_TYPE) / sizeof(T)};
    static_assert(sizeof(VECTOR_TYPE) % sizeof(T) == 0U);
    static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
    static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
    constexpr size_t VECTORIZED_BLOCK_TILE_SIZE_K{BLOCK_TILE_SIZE_K /
                                                  NUM_VECTOR_UNITS};
    static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
    constexpr size_t VECTORIZED_BLOCK_TILE_SIZE_X{BLOCK_TILE_SIZE_X /
                                                  NUM_VECTOR_UNITS};
    static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);

    // The skew size could affect the data alignment in shared memory when we use vectorized load.
    // We need to make sure the data alignment is correct.
    static_assert((BLOCK_TILE_SIZE_Y) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
    static_assert((BLOCK_TILE_SIZE_X) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
    static_assert((BLOCK_TILE_SIZE_Y + BLOCK_TILE_SKEW_SIZE_Y) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);
    static_assert((BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X) * sizeof(T) % sizeof(VECTOR_TYPE) == 0U);

// Load data from A on DRAM to A_thread_block_tile on shared memory.
#pragma unroll
    for (size_t load_idx{0U};
            load_idx < (BLOCK_TILE_SIZE_Y * VECTORIZED_BLOCK_TILE_SIZE_K +
                        NUM_THREADS - 1U) /
                        NUM_THREADS;
            ++load_idx)
    {
        size_t const A_thread_block_tile_row_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) /
            VECTORIZED_BLOCK_TILE_SIZE_K};
        size_t const A_thread_block_tile_col_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) %
            VECTORIZED_BLOCK_TILE_SIZE_K * NUM_VECTOR_UNITS};
        size_t const A_row_idx{blockIdx.y * BLOCK_TILE_SIZE_Y +
                                A_thread_block_tile_row_idx};
        size_t const A_col_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
                                A_thread_block_tile_col_idx};

        // These boundary checks might slow down the kernel to some extent.
        // But they guarantee the correctness of the kernel for all
        // different GEMM configurations.
        int4 A_row_vector_vals{0, 0, 0, 0};
        if (A_row_idx < m && A_col_idx < k)
        {
            A_row_vector_vals = *reinterpret_cast<int4 const*>(
                &A[A_row_idx * lda + A_col_idx]);
        }
        if (A_col_idx + NUM_VECTOR_UNITS > k)
        {
            // Number of invalid elements in the last vector.
            size_t const num_invalid_elements{A_col_idx + NUM_VECTOR_UNITS -
                                                k};
            // Mask out the invalid elements.
            T* const A_row_vector_vals_ptr{
                reinterpret_cast<T*>(&A_row_vector_vals)};
            for (size_t i{0U}; i < num_invalid_elements; ++i)
            {
                A_row_vector_vals_ptr[NUM_VECTOR_UNITS - 1U - i] =
                    static_cast<T>(0);
            }
        }
        // If this is true, the following if can be removed.
        // static_assert(VECTORIZED_BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y %
        // NUM_THREADS ==
        //               0U);
        if (A_thread_block_tile_row_idx < BLOCK_TILE_SIZE_Y &&
            A_thread_block_tile_col_idx < BLOCK_TILE_SIZE_K)
        {
            for (size_t i{0U}; i < NUM_VECTOR_UNITS; ++i)
            {
                A_thread_block_tile_transposed
                    [A_thread_block_tile_col_idx + i]
                    [A_thread_block_tile_row_idx] =
                        reinterpret_cast<T const*>(&A_row_vector_vals)[i];
            }
        }
    }
// Load data from B on DRAM to B_thread_block_tile on shared memory.
#pragma unroll
    for (size_t load_idx{0U};
            load_idx < (BLOCK_TILE_SIZE_K * VECTORIZED_BLOCK_TILE_SIZE_X +
                        NUM_THREADS - 1U) /
                        NUM_THREADS;
            ++load_idx)
    {
        size_t const B_thread_block_tile_row_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) /
            VECTORIZED_BLOCK_TILE_SIZE_X};
        size_t const B_thread_block_tile_col_idx{
            (thread_linear_idx + load_idx * NUM_THREADS) %
            VECTORIZED_BLOCK_TILE_SIZE_X * NUM_VECTOR_UNITS};
        size_t const B_row_idx{thread_block_tile_idx * BLOCK_TILE_SIZE_K +
                                B_thread_block_tile_row_idx};
        size_t const B_col_idx{blockIdx.x * BLOCK_TILE_SIZE_X +
                                B_thread_block_tile_col_idx};

        // These boundary checks might slow down the kernel to some extent.
        // But they guarantee the correctness of the kernel for all
        // different GEMM configurations.
        int4 B_row_vector_vals{0, 0, 0, 0};
        if (B_row_idx < k && B_col_idx < n)
        {
            B_row_vector_vals = *reinterpret_cast<int4 const*>(
                &B[B_row_idx * ldb + B_col_idx]);
        }
        if (B_col_idx + NUM_VECTOR_UNITS > n)
        {
            // Number of invalid elements in the last vector.
            size_t const num_invalid_elements{B_col_idx + NUM_VECTOR_UNITS -
                                                n};
            // Mask out the invalid elements.
            T* const B_row_vector_vals_ptr{
                reinterpret_cast<T*>(&B_row_vector_vals)};
            for (size_t i{0U}; i < num_invalid_elements; ++i)
            {
                B_row_vector_vals_ptr[NUM_VECTOR_UNITS - 1U - i] =
                    static_cast<T>(0);
            }
        }
        // If this is true, the following if can be removed.
        // static_assert(VECTORIZED_BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K %
        // NUM_THREADS ==
        //               0U);
        if (B_thread_block_tile_row_idx < BLOCK_TILE_SIZE_K &&
            B_thread_block_tile_col_idx < BLOCK_TILE_SIZE_X)
        {
            *reinterpret_cast<int4*>(
                &B_thread_block_tile[B_thread_block_tile_row_idx]
                                    [B_thread_block_tile_col_idx]) =
                B_row_vector_vals;
        }
    }
}

// GEMM kernel v05.
// Coalesced read and write from global memory.
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t THREAD_TILE_SIZE_X,
          size_t THREAD_TILE_SIZE_Y>
__global__ void gemm_v05_vectorized(size_t m, size_t n, size_t k, T alpha,
                                    T const* A, size_t lda, T const* B,
                                    size_t ldb, T beta, T* C, size_t ldc)
{
    // Avoid using blockDim.x * blockDim.y as the number of threads per block.
    // Because it is a runtime constant and the compiler cannot optimize the
    // loop unrolling based on that.
    // Use a compile time constant instead.
    constexpr size_t NUM_THREADS{BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
                                 (THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
    size_t const thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};

    // Cache a tile of A and B in shared memory for data reuse.
    __shared__ T
        A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_Y];
    __shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];

    size_t const num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
                                        BLOCK_TILE_SIZE_K};

    // Each thread in the block processes BLOCK_TILE_SIZE_Y output values.
    // Specifically, these values corresponds to
    // C[blockIdx.y * BLOCK_TILE_SIZE_Y + threadIdx.x / BLOCK_TILE_SIZE_X *
    // THREAD_TILE_SIZE_Y : blockIdx.y * BLOCK_TILE_SIZE_Y + (threadIdx.x /
    // BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_Y][blockIdx.x *
    // BLOCK_TILE_SIZE_X + threadIdx.x % BLOCK_TILE_SIZE_X *
    // THREAD_TILE_SIZE_X : blockIdx.x * BLOCK_TILE_SIZE_X + (threadIdx.x %
    // BLOCK_TILE_SIZE_X + 1) * THREAD_TILE_SIZE_X]
    T C_thread_results[THREAD_TILE_SIZE_Y][THREAD_TILE_SIZE_X] = {
        static_cast<T>(0)};
    // A_vals is cached in the register.
    T A_vals[THREAD_TILE_SIZE_Y] = {static_cast<T>(0)};
    // B_vals is cached in the register.
    T B_vals[THREAD_TILE_SIZE_X] = {static_cast<T>(0)};

    constexpr size_t NUM_VECTOR_UNITS{sizeof(int4) / sizeof(T)};
    static_assert(sizeof(int4) % sizeof(T) == 0U);
    static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
    static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
    constexpr size_t VECTORIZED_THREAD_TILE_SIZE_X{THREAD_TILE_SIZE_X /
                                                   NUM_VECTOR_UNITS};
    static_assert(THREAD_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);

    for (size_t thread_block_tile_idx{0U};
         thread_block_tile_idx < num_thread_block_tiles;
         ++thread_block_tile_idx)
    {
        load_data_to_shared_memory_transposed_vectorized<
            T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
            NUM_THREADS>(A, lda, B, ldb, A_thread_block_tile_transposed,
                         B_thread_block_tile, thread_block_tile_idx,
                         thread_linear_idx, m, n, k);
        __syncthreads();

#pragma unroll
        for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
        {
            size_t const A_thread_block_tile_row_idx{
                thread_linear_idx / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                THREAD_TILE_SIZE_Y};
            size_t const A_thread_block_tile_col_idx{k_i};

#pragma unroll
            for (size_t thread_tile_row_idx{0U};
                 thread_tile_row_idx < THREAD_TILE_SIZE_Y;
                 ++thread_tile_row_idx)
            {
                A_vals[thread_tile_row_idx] =
                    A_thread_block_tile_transposed[A_thread_block_tile_col_idx]
                                                  [A_thread_block_tile_row_idx +
                                                   thread_tile_row_idx];
            }

            size_t const B_thread_block_tile_row_idx{k_i};
            size_t const B_thread_block_tile_col_idx{
                thread_linear_idx % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                THREAD_TILE_SIZE_X};
// Although the read from A_thread_block_tile cannot be vectorized, the read
// from B_thread_block_tile can be vectorized.
#pragma unroll
            for (size_t thread_tile_col_vector_idx{0U};
                 thread_tile_col_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
                 ++thread_tile_col_vector_idx)
            {
                *reinterpret_cast<int4*>(
                    &B_vals[thread_tile_col_vector_idx * NUM_VECTOR_UNITS]) =
                    *reinterpret_cast<int4 const*>(
                        &B_thread_block_tile[B_thread_block_tile_row_idx]
                                            [B_thread_block_tile_col_idx +
                                             thread_tile_col_vector_idx *
                                                 NUM_VECTOR_UNITS]);
            }

            for (size_t thread_tile_row_idx{0U};
                 thread_tile_row_idx < THREAD_TILE_SIZE_Y;
                 ++thread_tile_row_idx)
            {
                for (size_t thread_tile_col_idx{0U};
                     thread_tile_col_idx < THREAD_TILE_SIZE_X;
                     ++thread_tile_col_idx)
                {
                    C_thread_results[thread_tile_row_idx]
                                    [thread_tile_col_idx] +=
                        A_vals[thread_tile_row_idx] *
                        B_vals[thread_tile_col_idx];
                }
            }
        }
        __syncthreads();
    }

    // Vectorized writing the results to DRAM.
    for (size_t thread_tile_row_idx{0U};
         thread_tile_row_idx < THREAD_TILE_SIZE_Y; ++thread_tile_row_idx)
    {
        for (size_t thread_tile_col_vector_idx{0U};
             thread_tile_col_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
             ++thread_tile_col_vector_idx)
        {
            size_t const C_row_idx{
                blockIdx.y * BLOCK_TILE_SIZE_Y +
                thread_linear_idx / (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                    THREAD_TILE_SIZE_Y +
                thread_tile_row_idx};
            size_t const C_col_idx{
                blockIdx.x * BLOCK_TILE_SIZE_X +
                thread_linear_idx % (BLOCK_TILE_SIZE_X / THREAD_TILE_SIZE_X) *
                    THREAD_TILE_SIZE_X +
                thread_tile_col_vector_idx * NUM_VECTOR_UNITS};
            // Vectorized read from C.
            int4 C_row_vector_vals{*reinterpret_cast<int4 const*>(
                &C[C_row_idx * ldc + C_col_idx])};
            // Vectorized read from C_thread_results.
            int4 const C_thread_results_row_vector_vals{
                *reinterpret_cast<int4 const*>(
                    &C_thread_results[thread_tile_row_idx]
                                     [thread_tile_col_vector_idx *
                                      NUM_VECTOR_UNITS])};
            // Update the values in C_row_vector_vals
            for (size_t i{0U}; i < NUM_VECTOR_UNITS; ++i)
            {
                reinterpret_cast<T*>(&C_row_vector_vals)[i] =
                    alpha * reinterpret_cast<T const*>(
                                &C_thread_results_row_vector_vals)[i] +
                    beta * reinterpret_cast<T const*>(&C_row_vector_vals)[i];
            }
            // Vectorized write to C.
            if (C_row_idx < m && C_col_idx < n)
            {
                // No need to mask out the out-of-bound invalid elements,
                // because the row of C matrix is 32-byte aligned.
                *reinterpret_cast<int4*>(&C[C_row_idx * ldc + C_col_idx]) =
                    C_row_vector_vals;
            }
        }
    }
}

template <typename T>
void launch_gemm_kernel_v05_vectorized(size_t m, size_t n, size_t k,
                                       T const* alpha, T const* A, size_t lda,
                                       T const* B, size_t ldb, T const* beta,
                                       T* C, size_t ldc, cudaStream_t stream)
{
    // Feel free to play with the block tile sizes.
    // The algorithm correctness should always be guaranteed.
    constexpr unsigned int BLOCK_TILE_SIZE_X{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_Y{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_K{16U};
    // Each thread computes THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y values of C.
    constexpr unsigned int THREAD_TILE_SIZE_X{8U};
    constexpr unsigned int THREAD_TILE_SIZE_Y{8U};
    constexpr unsigned int NUM_THREADS_PER_BLOCK{
        BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_Y /
        (THREAD_TILE_SIZE_X * THREAD_TILE_SIZE_Y)};
    static_assert(BLOCK_TILE_SIZE_X % THREAD_TILE_SIZE_X == 0U);
    static_assert(BLOCK_TILE_SIZE_Y % THREAD_TILE_SIZE_Y == 0U);
    static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_K == 0U);
    static_assert(NUM_THREADS_PER_BLOCK % BLOCK_TILE_SIZE_X == 0U);
    static_assert(
        BLOCK_TILE_SIZE_X * BLOCK_TILE_SIZE_K % NUM_THREADS_PER_BLOCK == 0U);
    static_assert(
        BLOCK_TILE_SIZE_K * BLOCK_TILE_SIZE_Y % NUM_THREADS_PER_BLOCK == 0U);
    dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + BLOCK_TILE_SIZE_X - 1U) /
            BLOCK_TILE_SIZE_X,
        (static_cast<unsigned int>(m) + BLOCK_TILE_SIZE_Y - 1U) /
            BLOCK_TILE_SIZE_Y,
        1U};
    gemm_v05_vectorized<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
                        BLOCK_TILE_SIZE_K, THREAD_TILE_SIZE_X,
                        THREAD_TILE_SIZE_Y>
        <<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
                                              *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

Except the data loading using vectorized memory access, the rest of the kernel is the same as the previous implementation with 2D block tiling and 2D thread tiling. There is, however, a caveat for vectorized memory access in our use case which does not exist in the previous implementation. When we load the data from global memory to the shared memory and load the data from the shared memory to the registers, considering the matrices are 2D, we need to make sure the data alignment is correct for the vectorized memory access data type. Otherwise, undefined behavior will happen. For example, if we use int4 as the vectorized memory access data type, we need to make sure the data alignment is a multiple of 16 bytes. This is why we will have to pad the leading dimension of the matrix $A$ and matrix $B$ in the global memory and the shared memory dimensions have to be carefully chosen.

The performance of this FP32 GEMM implementation becomes 19.66 TFLOPS on an NVIDIA GeForce RTX 3090 GPU.

Implementation with 2D Block Tiling and 2D Warp Tiling and 2D Thread Tiling and Vectorized Memory Access

In the CUDA programming model, a warp, which consists of 32 threads, is the smallest unit of scheduling and execution. Shared memory bank conflicts can happen when the threads in a warp access the same bank of the shared memory. In our previous implementation, because the GEMM CUDA kernel was not organized in a warp-centric way, it is less obvious how to avoid shared memory bank conflicts.

In this implementation, we will organize the GEMM CUDA kernel in a warp-centric way and use 2D warp tiling and 2D thread tiling so that the shared memory bank conflicts can be anticipated and optimized much easier.

Understanding warp tiling is almost exactly the same as understanding thread tiling.

Mathematically, given a matrix multiplication and accumulation operation $D_{b_m,b_n}^{d_{bm} \times d_{bn}} = \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}}$, where $D_{b_m,b_n} \in \mathbb{R}^{d_{bm} \times d_{bn}}$, $A_{b_m,b_k} \in \mathbb{R}^{d_{bm} \times d_{bk}}$, $B_{b_k,b_n} \in \mathbb{R}^{d_{bk} \times d_{bn}}$, $C_{b_m,b_n} \in \mathbb{R}^{d_{bm} \times d_{bn}}$, the matrices could be divided into smaller matrices.

$$
A_{b_m,b_k}^{d_{bm} \times d_{bk}} =
\begin{bmatrix}
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,1}^{d_{wm} \times d_{wk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,2}^{d_{wm} \times d_{wk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,d_{bk}/d_{wk}}^{d_{wm} \times d_{wk}} \\
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,1}^{d_{wm} \times d_{wk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,2}^{d_{wm} \times d_{wk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,d_{bk}/d_{wk}}^{d_{wm} \times d_{wk}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{wm},1}^{d_{wm} \times d_{wk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{wm},2}^{d_{wm} \times d_{wk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{wm},d_{bk}/d_{wk}}^{d_{wm} \times d_{wk}} \\
\end{bmatrix}
$$

$$
B_{b_k,b_n}^{d_{bk} \times d_{bn}} =
\begin{bmatrix}
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,1}^{d_{wk} \times d_{wn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,2}^{d_{wk} \times d_{wn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,d_{bn}/d_{wn}}^{d_{wk} \times d_{wn}} \\
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,1}^{d_{wk} \times d_{wn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,2}^{d_{wk} \times d_{wn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,d_{bn}/d_{wn}}^{d_{wk} \times d_{wn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{wk},1}^{d_{wk} \times d_{wn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{wk},2}^{d_{wk} \times d_{wn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{wk},d_{bn}/d_{wn}}^{d_{wk} \times d_{wn}} \\
\end{bmatrix}
$$

$$
C_{b_m,b_n}^{d_{bm} \times d_{bn}} =
\begin{bmatrix}
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,1}^{d_{wm} \times d_{wn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,2}^{d_{wm} \times d_{wn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,1}^{d_{wm} \times d_{wn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,2}^{d_{wm} \times d_{wn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},1}^{d_{wm} \times d_{wn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},2}^{d_{wm} \times d_{wn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\end{bmatrix}
$$

$$
D_{b_m,b_n}^{d_{bm} \times d_{bn}} =
\begin{bmatrix}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,1}^{d_{wm} \times d_{wn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,2}^{d_{wm} \times d_{wn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,1}^{d_{wm} \times d_{wn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,2}^{d_{wm} \times d_{wn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},1}^{d_{wm} \times d_{wn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},2}^{d_{wm} \times d_{wn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\end{bmatrix}
$$

Each small matrix in $D_{b_m,b_n}^{d_{bm} \times d_{bn}}$ is computed as multiple small matrix multiplications and accumulations.

$$
\begin{aligned}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}
&= \left( \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{w_k=1}^{d_{bk} / d_{wk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} \\
\end{aligned}
$$

Each warp with block warp index $(w_m, w_n)$, where $w_m \in [1, d_{bm} / d_{wm}]$ and $w_n \in [1, d_{bn} / d_{wn}]$, in the block with block index $(b_m, b_n)$, where $b_m \in [1, m/d_{bm}]$ and $b_n \in [1, n/d_{bn}]$, is responsible for computing one small matrix multiplication and accumulation $\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}$.

So far, everything looks the same as the mathematical descriptions for the 2D thread tiling, except that the thread indices and thread tile sizes are replaced by the warp indices and warp tile sizes.

The remaining question is how to use all the 32 threads in the warp with block warp index $(w_m, w_n)$ to compute $\left(\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}\right)^{d_{wm} \times d_{wn}}$. There is not a unique way to do that. The way we chose is to use 2D thread tiling. Suppose the number of threads per warp in the row is $m_{t}$ and the number of threads per warp in the column is $n_{t}$, we must have $m_{t} \times n_{t} = 32$. Each thread in the warp should be responsible for computing $\left(d_{wm} / m_{t}) \times (d_{wn} / n_{t}\right)$ values of the output matrix $\left(\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}\right)^{d_{wm} \times d_{wn}}$. We then set the thread tile sizes to be $d_{tm}$ for row and $d_{tn}$ for column, such that $\left(d_{wm} / m_{t} \right) \mod d_{tm} = 0$ and $\left(d_{wn} / n_{t} \right) \mod d_{tn} = 0$. Each thread in the warp will have to compute $\left(\left(d_{wm} / m_{t} \right) / d_{tm} \right) \times \left(\left(d_{wn} / n_{t} \right) / d_{tn} \right)$ tiles of size $d_{tm} \times d_{tn}$ of the output matrix $\left(\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}\right)^{d_{wm} \times d_{wn}}$.

Suppose the thread tile index is $(t_m, t_n)$, where $t_m \in [1, d_{wm} / d_{tm}]$ and $t_n \in [1, d_{wn} / d_{tn}]$. The thread responsible for computing the tile has the warp thread index $(t_m \mod m_t, t_n \mod n_t)$. Because the matrix $\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}}$ can be divided along the row dimension to $d_{wm} / d_{tm}$ fragments and the matrix $\left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}$ can be divided along the column dimension to $d_{wn} / d_{tn}$ fragments. We have

$$
\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} =
\begin{bmatrix}
\left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{1,1}^{d_{tm} \times d_{tk}} & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{1,2}^{d_{tm} \times d_{tk}} & \cdots & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{1,d_{wk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{2,1}^{d_{tm} \times d_{tk}} & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{2,2}^{d_{tm} \times d_{tk}} & \cdots & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{2,d_{wk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\vdots & \vdots & \ddots & \vdots \\
\left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{d_{wm}/d_{tm},1}^{d_{tm} \times d_{tk}} & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{d_{wm}/d_{tm},2}^{d_{tm} \times d_{tk}} & \cdots & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{d_{wm}/d_{tm},d_{wk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\end{bmatrix}
$$

$$
\left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} =
\begin{bmatrix}
\left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{1,1}^{d_{tk} \times d_{tn}} & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{1,2}^{d_{tk} \times d_{tn}} & \cdots & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{1,d_{wn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{2,1}^{d_{tk} \times d_{tn}} & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{2,2}^{d_{tk} \times d_{tn}} & \cdots & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{2,d_{wn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{d_{wk}/d_{tk},1}^{d_{tk} \times d_{tn}} & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{d_{wk}/d_{tk},2}^{d_{tk} \times d_{tn}} & \cdots & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{d_{wk}/d_{tk},d_{wn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\end{bmatrix}
$$

Each thread with warp thread index $(t_m \mod m_t, t_n \mod n_t)$ is responsible for computing one small matrix multiplication and accumulation $\left(\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}$.

The thread tile $\left(\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}$ can be computed as follows.

$$
\begin{aligned}
\left(\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}
&= \sum_{t_k=1}^{d_{wk} / d_{tk}} \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{t_m,t_k}^{d_{tm} \times d_{tk}} \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{t_k,t_n}^{d_{tk} \times d_{tn}} \\
\end{aligned}
$$

Taken together, the thread tile $\left(\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}$ can be computed as follows.

$$
\begin{aligned}
\left(\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}
&= \left(\sum_{b_k=1}^{k/d_{bk}} \left( \sum_{w_k=1}^{d_{bk} / d_{wk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{w_k=1}^{d_{bk} / d_{wk}} \left( \sum_{t_k=1}^{d_{wk} / d_{tk}} \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{t_m,t_k}^{d_{tm} \times d_{tk}} \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{t_k,t_n}^{d_{tk} \times d_{tn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}} \\
\end{aligned}
$$

In this implementation, we set $d_{wk} = d_{tk}$ to make the thread tiling algorithm simpler.

The following code snippet shows the implementation with 2D block tiling and 2D warp tiling and 2D thread tiling and vectorized memory access.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
// GEMM kernel v06.
// Each thread in the block processes THREAD_TILE_SIZE_Y *
// THREAD_TILE_SIZE_X output values. Number of threads BLOCK_TILE_SIZE_Y *
// BLOCK_TILE_SIZE_X / (THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X)
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t WARP_TILE_SIZE_X,
          size_t WARP_TILE_SIZE_Y, size_t THREAD_TILE_SIZE_X,
          size_t THREAD_TILE_SIZE_Y, size_t NUM_THREADS_PER_WARP_X,
          size_t NUM_THREADS_PER_WARP_Y>
__global__ void gemm_v06_vectorized(size_t m, size_t n, size_t k, T alpha,
                                    T const* A, size_t lda, T const* B,
                                    size_t ldb, T beta, T* C, size_t ldc)
{
    static_assert(NUM_THREADS_PER_WARP_X * NUM_THREADS_PER_WARP_Y == 32U);
    constexpr size_t NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
    static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
    constexpr size_t NUM_WARPS_Y{BLOCK_TILE_SIZE_Y / WARP_TILE_SIZE_Y};
    static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);
    constexpr unsigned int NUM_THREAD_TILES_PER_WARP_X{
        WARP_TILE_SIZE_X / (THREAD_TILE_SIZE_X * NUM_THREADS_PER_WARP_X)};
    constexpr unsigned int NUM_THREAD_TILES_PER_WARP_Y{
        WARP_TILE_SIZE_Y / (THREAD_TILE_SIZE_Y * NUM_THREADS_PER_WARP_Y)};
    static_assert(
        WARP_TILE_SIZE_X % (THREAD_TILE_SIZE_X * NUM_THREADS_PER_WARP_X) == 0U);
    static_assert(
        WARP_TILE_SIZE_Y % (THREAD_TILE_SIZE_Y * NUM_THREADS_PER_WARP_Y) == 0U);

    constexpr unsigned int NUM_THREADS_X{NUM_WARPS_X * NUM_THREADS_PER_WARP_X};
    constexpr unsigned int NUM_THREADS_Y{NUM_WARPS_Y * NUM_THREADS_PER_WARP_Y};
    // Avoid using blockDim.x * blockDim.y as the number of threads per block.
    // Because it is a runtime constant and the compiler cannot optimize the
    // loop unrolling based on that.
    // Use a compile time constant instead.
    constexpr size_t NUM_THREADS{NUM_THREADS_X * NUM_THREADS_Y};

    // Cache a tile of A and B in shared memory for data reuse.
    __shared__ T
        A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_Y];
    __shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X];

    // A_vals is cached in the register.
    T A_vals[NUM_THREAD_TILES_PER_WARP_Y][THREAD_TILE_SIZE_Y] = {
        static_cast<T>(0)};
    // B_vals is cached in the register.
    T B_vals[NUM_THREAD_TILES_PER_WARP_X][THREAD_TILE_SIZE_X] = {
        static_cast<T>(0)};

    size_t const thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
    size_t const warp_linear_idx{thread_linear_idx / 32U};
    size_t const warp_row_idx{warp_linear_idx / NUM_WARPS_X};
    size_t const warp_col_idx{warp_linear_idx % NUM_WARPS_X};
    size_t const thread_linear_idx_in_warp{thread_linear_idx % 32U};
    size_t const thread_linear_row_idx_in_warp{thread_linear_idx_in_warp /
                                               NUM_THREADS_PER_WARP_X};
    size_t const thread_linear_col_idx_in_warp{thread_linear_idx_in_warp %
                                               NUM_THREADS_PER_WARP_X};

    // Number of outer loops to perform the sum of inner products.
    // C_thread_block_tile =
    // \sigma_{thread_block_tile_idx=0}^{num_thread_block_tiles-1} A[:,
    // thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
    // B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :]
    size_t const num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
                                        BLOCK_TILE_SIZE_K};
    // Each thread in the block processes NUM_THREAD_TILES_PER_WARP_Y *
    // NUM_THREAD_TILES_PER_WARP_X * THREAD_TILE_SIZE_Y *
    // THREAD_TILE_SIZE_X output values.
    T C_thread_results[NUM_THREAD_TILES_PER_WARP_Y][NUM_THREAD_TILES_PER_WARP_X]
                      [THREAD_TILE_SIZE_Y][THREAD_TILE_SIZE_X] = {
                          static_cast<T>(0)};

    constexpr size_t NUM_VECTOR_UNITS{sizeof(int4) / sizeof(T)};
    static_assert(sizeof(int4) % sizeof(T) == 0U);
    static_assert(BLOCK_TILE_SIZE_K % NUM_VECTOR_UNITS == 0U);
    static_assert(BLOCK_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
    constexpr size_t VECTORIZED_THREAD_TILE_SIZE_X{THREAD_TILE_SIZE_X /
                                                   NUM_VECTOR_UNITS};
    static_assert(THREAD_TILE_SIZE_X % NUM_VECTOR_UNITS == 0U);
    constexpr size_t VECTORIZED_THREAD_TILE_SIZE_Y{THREAD_TILE_SIZE_Y /
                                                   NUM_VECTOR_UNITS};
    static_assert(THREAD_TILE_SIZE_Y % NUM_VECTOR_UNITS == 0U);

    for (size_t thread_block_tile_idx{0U};
         thread_block_tile_idx < num_thread_block_tiles;
         ++thread_block_tile_idx)
    {
        load_data_to_shared_memory_transposed_vectorized<
            T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
            NUM_THREADS>(A, lda, B, ldb, A_thread_block_tile_transposed,
                         B_thread_block_tile, thread_block_tile_idx,
                         thread_linear_idx, m, n, k);
        __syncthreads();

// Perform A[:, thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :] where A[:,
// thread_block_tile_idx:BLOCK_TILE_SIZE_K] and
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :] are cached in the
// shared memory as A_thread_block_tile and B_thread_block_tile,
// respectively. This inner product is further decomposed to
// BLOCK_TILE_SIZE_K outer products. A_thread_block_tile *
// B_thread_block_tile = \sigma_{k_i=0}^{BLOCK_TILE_SIZE_K-1}
// A_thread_block_tile[:, k_i] @ B_thread_block_tile[k_i, :] Note that
// both A_thread_block_tile and B_thread_block_tile can be cached in the
// register.
#pragma unroll
        for (size_t k_i{0U}; k_i < BLOCK_TILE_SIZE_K; ++k_i)
        {
#pragma unroll
            for (size_t thread_tile_repeat_row_idx{0U};
                 thread_tile_repeat_row_idx < NUM_THREAD_TILES_PER_WARP_Y;
                 ++thread_tile_repeat_row_idx)
            {
                size_t const A_thread_block_tile_row_idx{
                    warp_row_idx * WARP_TILE_SIZE_Y +
                    thread_tile_repeat_row_idx *
                        (WARP_TILE_SIZE_Y / NUM_THREAD_TILES_PER_WARP_Y) +
                    thread_linear_row_idx_in_warp * THREAD_TILE_SIZE_Y};
                size_t const A_thread_block_tile_col_idx{k_i};
#pragma unroll
                for (size_t thread_tile_y_vector_idx{0U};
                     thread_tile_y_vector_idx < VECTORIZED_THREAD_TILE_SIZE_Y;
                     ++thread_tile_y_vector_idx)
                {
                    *reinterpret_cast<int4*>(
                        &A_vals[thread_tile_repeat_row_idx]
                               [thread_tile_y_vector_idx * NUM_VECTOR_UNITS]) =
                        *reinterpret_cast<int4 const*>(
                            &A_thread_block_tile_transposed
                                [A_thread_block_tile_col_idx]
                                [A_thread_block_tile_row_idx +
                                 thread_tile_y_vector_idx * NUM_VECTOR_UNITS]);
                }
            }
#pragma unroll
            for (size_t thread_tile_repeat_col_idx{0U};
                 thread_tile_repeat_col_idx < NUM_THREAD_TILES_PER_WARP_X;
                 ++thread_tile_repeat_col_idx)
            {
                size_t const B_thread_block_tile_row_idx{k_i};
                size_t const B_thread_block_tile_col_idx{
                    warp_col_idx * WARP_TILE_SIZE_X +
                    thread_tile_repeat_col_idx *
                        (WARP_TILE_SIZE_X / NUM_THREAD_TILES_PER_WARP_X) +
                    thread_linear_col_idx_in_warp * THREAD_TILE_SIZE_X};
#pragma unroll
                for (size_t thread_tile_x_vector_idx{0U};
                     thread_tile_x_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
                     ++thread_tile_x_vector_idx)
                {
                    *reinterpret_cast<int4*>(
                        &B_vals[thread_tile_repeat_col_idx]
                               [thread_tile_x_vector_idx * NUM_VECTOR_UNITS]) =
                        *reinterpret_cast<int4 const*>(
                            &B_thread_block_tile[B_thread_block_tile_row_idx]
                                                [B_thread_block_tile_col_idx +
                                                 thread_tile_x_vector_idx *
                                                     NUM_VECTOR_UNITS]);
                }
            }

// Compute NUM_THREAD_TILES_PER_WARP_Y * NUM_THREAD_TILES_PER_WARP_X outer
// products.
#pragma unroll
            for (size_t thread_tile_repeat_row_idx{0U};
                 thread_tile_repeat_row_idx < NUM_THREAD_TILES_PER_WARP_Y;
                 ++thread_tile_repeat_row_idx)
            {
#pragma unroll
                for (size_t thread_tile_repeat_col_idx{0U};
                     thread_tile_repeat_col_idx < NUM_THREAD_TILES_PER_WARP_X;
                     ++thread_tile_repeat_col_idx)
                {
#pragma unroll
                    for (size_t thread_tile_y_idx{0U};
                         thread_tile_y_idx < THREAD_TILE_SIZE_Y;
                         ++thread_tile_y_idx)
                    {
#pragma unroll
                        for (size_t thread_tile_x_idx{0U};
                             thread_tile_x_idx < THREAD_TILE_SIZE_X;
                             ++thread_tile_x_idx)
                        {
                            C_thread_results[thread_tile_repeat_row_idx]
                                            [thread_tile_repeat_col_idx]
                                            [thread_tile_y_idx]
                                            [thread_tile_x_idx] +=
                                A_vals[thread_tile_repeat_row_idx]
                                      [thread_tile_y_idx] *
                                B_vals[thread_tile_repeat_col_idx]
                                      [thread_tile_x_idx];
                        }
                    }
                }
            }
        }
        __syncthreads();
    }

// Write the results to DRAM.
#pragma unroll
    for (size_t thread_tile_repeat_row_idx{0U};
         thread_tile_repeat_row_idx < NUM_THREAD_TILES_PER_WARP_Y;
         ++thread_tile_repeat_row_idx)
    {
#pragma unroll
        for (size_t thread_tile_repeat_col_idx{0U};
             thread_tile_repeat_col_idx < NUM_THREAD_TILES_PER_WARP_X;
             ++thread_tile_repeat_col_idx)
        {
#pragma unroll
            for (size_t thread_tile_y_idx{0U};
                 thread_tile_y_idx < THREAD_TILE_SIZE_Y; ++thread_tile_y_idx)
            {
#pragma unroll
                for (size_t thread_tile_x_vector_idx{0U};
                     thread_tile_x_vector_idx < VECTORIZED_THREAD_TILE_SIZE_X;
                     ++thread_tile_x_vector_idx)
                {
                    size_t const C_row_idx{
                        blockIdx.y * BLOCK_TILE_SIZE_Y +
                        warp_row_idx * WARP_TILE_SIZE_Y +
                        thread_tile_repeat_row_idx *
                            (WARP_TILE_SIZE_Y / NUM_THREAD_TILES_PER_WARP_Y) +
                        thread_linear_row_idx_in_warp * THREAD_TILE_SIZE_Y +
                        thread_tile_y_idx};
                    size_t const C_col_idx{
                        blockIdx.x * BLOCK_TILE_SIZE_X +
                        warp_col_idx * WARP_TILE_SIZE_X +
                        thread_tile_repeat_col_idx *
                            (WARP_TILE_SIZE_X / NUM_THREAD_TILES_PER_WARP_X) +
                        thread_linear_col_idx_in_warp * THREAD_TILE_SIZE_X +
                        thread_tile_x_vector_idx * NUM_VECTOR_UNITS};

                    if (C_row_idx < m && C_col_idx < n)
                    {
                        int4 C_vals{*reinterpret_cast<int4 const*>(
                            &C[C_row_idx * ldc + C_col_idx])};
#pragma unroll
                        for (size_t i{0U}; i < NUM_VECTOR_UNITS; ++i)
                        {
                            reinterpret_cast<T*>(&C_vals)[i] =
                                alpha *
                                    C_thread_results[thread_tile_repeat_row_idx]
                                                    [thread_tile_repeat_col_idx]
                                                    [thread_tile_y_idx]
                                                    [thread_tile_x_vector_idx *
                                                         NUM_VECTOR_UNITS +
                                                     i] +
                                beta * reinterpret_cast<T const*>(&C_vals)[i];
                        }
                        *reinterpret_cast<int4*>(
                            &C[C_row_idx * ldc + C_col_idx]) = C_vals;
                    }
                }
            }
        }
    }
}

template <typename T>
void launch_gemm_kernel_v06_vectorized(size_t m, size_t n, size_t k,
                                       T const* alpha, T const* A, size_t lda,
                                       T const* B, size_t ldb, T const* beta,
                                       T* C, size_t ldc, cudaStream_t stream)
{
    // Feel free to play with the block tile sizes.
    // The algorithm correctness should always be guaranteed.
    constexpr unsigned int BLOCK_TILE_SIZE_X{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_Y{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_K{16U};

    constexpr unsigned int WARP_TILE_SIZE_X{32U};
    constexpr unsigned int WARP_TILE_SIZE_Y{64U};
    constexpr unsigned int NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
    constexpr unsigned int NUM_WARPS_Y{BLOCK_TILE_SIZE_Y / WARP_TILE_SIZE_Y};
    static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
    static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);

    constexpr unsigned int THREAD_TILE_SIZE_X{8U};
    constexpr unsigned int THREAD_TILE_SIZE_Y{8U};

    constexpr unsigned int NUM_THREADS_PER_WARP_X{4U};
    constexpr unsigned int NUM_THREADS_PER_WARP_Y{8U};
    static_assert(NUM_THREADS_PER_WARP_X * NUM_THREADS_PER_WARP_Y == 32U);
    static_assert(
        WARP_TILE_SIZE_X % (THREAD_TILE_SIZE_X * NUM_THREADS_PER_WARP_X) == 0U);
    static_assert(
        WARP_TILE_SIZE_Y % (THREAD_TILE_SIZE_Y * NUM_THREADS_PER_WARP_Y) == 0U);

    constexpr unsigned int NUM_THREADS_X{NUM_WARPS_X * NUM_THREADS_PER_WARP_X};
    constexpr unsigned int NUM_THREADS_Y{NUM_WARPS_Y * NUM_THREADS_PER_WARP_Y};

    constexpr unsigned int NUM_THREADS_PER_BLOCK{NUM_THREADS_X * NUM_THREADS_Y};

    dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + BLOCK_TILE_SIZE_X - 1U) /
            BLOCK_TILE_SIZE_X,
        (static_cast<unsigned int>(m) + BLOCK_TILE_SIZE_Y - 1U) /
            BLOCK_TILE_SIZE_Y,
        1U};
    gemm_v06_vectorized<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
                        BLOCK_TILE_SIZE_K, WARP_TILE_SIZE_X, WARP_TILE_SIZE_Y,
                        THREAD_TILE_SIZE_X, THREAD_TILE_SIZE_Y,
                        NUM_THREADS_PER_WARP_X, NUM_THREADS_PER_WARP_Y>
        <<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
                                              *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

The performance of this FP32 GEMM implementation becomes 20.16 TFLOPS on an NVIDIA GeForce RTX 3090 GPU. Comparing to the cuBLAS FP32 GEMM performance, which is 24.59 TFLOPS, this implementation has been optimized reasonably well.

Implementation with 2D Block Tiling and 2D Warp Tiling and Tensor Core and Vectorized Memory Access

Because we have already organized the GEMM CUDA kernel in a warp-centric way, and NVIDIA Tensor Core instructions are interfaced at the warp level, it is then very straightforward to utilize NVIDIA Tensor Core WMMA APIs to further accelerate the GEMM computation. Because the NVIDIA Tensor Core does not support IEEE FP32 computation, we will make this CUDA kernel to run FP16 GEMM instead.

Comparing to the implementation with 2D block tiling and 2D warp tiling and 2D thread tiling and vectorized memory access, the implementation with 2D block tiling and 2D warp tiling and Tensor Core and vectorized memory access is simpler because the thread tiling process is abstracted away by the NVIDIA Tensor Core warp-level WMMA APIs.

Mathematically, given a matrix multiplication and accumulation operation $D_{b_m,b_n}^{d_{bm} \times d_{bn}} = \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}}$, where $D_{b_m,b_n} \in \mathbb{R}^{d_{bm} \times d_{bn}}$, $A_{b_m,b_k} \in \mathbb{R}^{d_{bm} \times d_{bk}}$, $B_{b_k,b_n} \in \mathbb{R}^{d_{bk} \times d_{bn}}$, $C_{b_m,b_n} \in \mathbb{R}^{d_{bm} \times d_{bn}}$, the matrices could be divided into smaller matrices.

$$
A_{b_m,b_k}^{d_{bm} \times d_{bk}} =
\begin{bmatrix}
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,1}^{d_{wm} \times d_{wk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,2}^{d_{wm} \times d_{wk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{1,d_{bk}/d_{wk}}^{d_{wm} \times d_{wk}} \\
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,1}^{d_{wm} \times d_{wk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,2}^{d_{wm} \times d_{wk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{2,d_{bk}/d_{wk}}^{d_{wm} \times d_{wk}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{wm},1}^{d_{wm} \times d_{wk}} & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{wm},2}^{d_{wm} \times d_{wk}} & \cdots & \left(A_{b_m,b_k}^{d_{bm} \times d_{bk}}\right)_{d_{bm}/d_{wm},d_{bk}/d_{wk}}^{d_{wm} \times d_{wk}} \\
\end{bmatrix}
$$

$$
B_{b_k,b_n}^{d_{bk} \times d_{bn}} =
\begin{bmatrix}
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,1}^{d_{wk} \times d_{wn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,2}^{d_{wk} \times d_{wn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{1,d_{bn}/d_{wn}}^{d_{wk} \times d_{wn}} \\
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,1}^{d_{wk} \times d_{wn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,2}^{d_{wk} \times d_{wn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{2,d_{bn}/d_{wn}}^{d_{wk} \times d_{wn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{wk},1}^{d_{wk} \times d_{wn}} & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{wk},2}^{d_{wk} \times d_{wn}} & \cdots & \left(B_{b_k,b_n}^{d_{bk} \times d_{bn}}\right)_{d_{bk}/d_{wk},d_{bn}/d_{wn}}^{d_{wk} \times d_{wn}} \\
\end{bmatrix}
$$

$$
C_{b_m,b_n}^{d_{bm} \times d_{bn}} =
\begin{bmatrix}
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,1}^{d_{wm} \times d_{wn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,2}^{d_{wm} \times d_{wn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,1}^{d_{wm} \times d_{wn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,2}^{d_{wm} \times d_{wn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},1}^{d_{wm} \times d_{wn}} & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},2}^{d_{wm} \times d_{wn}} & \cdots & \left(C_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\end{bmatrix}
$$

$$
D_{b_m,b_n}^{d_{bm} \times d_{bn}} =
\begin{bmatrix}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,1}^{d_{wm} \times d_{wn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,2}^{d_{wm} \times d_{wn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{1,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,1}^{d_{wm} \times d_{wn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,2}^{d_{wm} \times d_{wn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{2,d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},1}^{d_{wm} \times d_{wn}} & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},2}^{d_{wm} \times d_{wn}} & \cdots & \left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{d_{bm}/d_{wm},d_{bn}/d_{wn}}^{d_{wm} \times d_{wn}} \\
\end{bmatrix}
$$

Each small matrix in $D_{b_m,b_n}^{d_{bm} \times d_{bn}}$ is computed as multiple small matrix multiplications and accumulations.

$$
\begin{aligned}
\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}
&= \left( \sum_{b_k=1}^{k/d_{bk}} A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} + C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{w_k=1}^{d_{bk} / d_{wk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}} \\
\end{aligned}
$$

Each warp with block warp index $(w_m, w_n)$, where $w_m \in [1, d_{bm} / d_{wm}]$ and $w_n \in [1, d_{bn} / d_{wn}]$, in the block with block index $(b_m, b_n)$, where $b_m \in [1, m/d_{bm}]$ and $b_n \in [1, n/d_{bn}]$, is responsible for computing one small matrix multiplication and accumulation $\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}$.

Suppose the Tensor Core WMMA GEMM size is $d_{tm} \times d_{tn} \times d_{tk}$. Because the matrix $\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}}$ can be divided along the row dimension to $d_{wm} / d_{tm}$ fragments and the matrix $\left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}}$ can be divided along the column dimension to $d_{wn} / d_{tn}$ fragments. We have

$$
\left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} =
\begin{bmatrix}
\left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{1,1}^{d_{tm} \times d_{tk}} & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{1,2}^{d_{tm} \times d_{tk}} & \cdots & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{1,d_{wk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{2,1}^{d_{tm} \times d_{tk}} & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{2,2}^{d_{tm} \times d_{tk}} & \cdots & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{2,d_{wk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\vdots & \vdots & \ddots & \vdots \\
\left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{d_{wm}/d_{tm},1}^{d_{tm} \times d_{tk}} & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{d_{wm}/d_{tm},2}^{d_{tm} \times d_{tk}} & \cdots & \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{d_{wm}/d_{tm},d_{wk}/d_{tk}}^{d_{tm} \times d_{tk}} \\
\end{bmatrix}
$$

$$
\left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} =
\begin{bmatrix}
\left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{1,1}^{d_{tk} \times d_{tn}} & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{1,2}^{d_{tk} \times d_{tn}} & \cdots & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{1,d_{wn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{2,1}^{d_{tk} \times d_{tn}} & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{2,2}^{d_{tk} \times d_{tn}} & \cdots & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{2,d_{wn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\vdots & \vdots & \ddots & \vdots \\
\left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{d_{wk}/d_{tk},1}^{d_{tk} \times d_{tn}} & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{d_{wk}/d_{tk},2}^{d_{tk} \times d_{tn}} & \cdots & \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{d_{wk}/d_{tk},d_{wn}/d_{tn}}^{d_{tk} \times d_{tn}} \\
\end{bmatrix}
$$

Instead of calling thread-level instructions, each warp will call WMMA warp-level Tensor Core to compute all the $\left(\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}$ for $\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}$ iteratively.

$$
\begin{aligned}
\left(\left(D_{b_m,b_n}^{d_{bm} \times d_{bn}}\right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}}
&= \left(\sum_{b_k=1}^{k/d_{bk}} \left( \sum_{w_k=1}^{d_{bk} / d_{wk}} \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}} \\
&= \sum_{b_k=1}^{k/d_{bk}} \left( \sum_{w_k=1}^{d_{bk} / d_{wk}} \left( \sum_{t_k=1}^{d_{wk} / d_{tk}} \left( \left( A_{b_m,b_k}^{d_{bm} \times d_{bk}} \right)_{w_m,w_k}^{d_{wm} \times d_{wk}} \right)_{t_m,t_k}^{d_{tm} \times d_{tk}} \left( \left( B_{b_k,b_n}^{d_{bk} \times d_{bn}} \right)_{w_k,w_n}^{d_{wk} \times d_{wn}} \right)_{t_k,t_n}^{d_{tk} \times d_{tn}} \right) + \left( C_{b_m,b_n}^{d_{bm} \times d_{bn}} \right)_{w_m,w_n}^{d_{wm} \times d_{wn}}\right)_{t_m, t_n}^{d_{tm} \times d_{tn}} \\
\end{aligned}
$$

In this implementation, because of the WMMA Tensor Core API restrictions, $d_{tm} = 16$, $d_{tn} = 16$, $d_{tk} = 16$.

The following code snippet shows the implementation with 2D block tiling and 2D warp tiling and Tensor Core and vectorized memory access.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
// GEMM kernel v07.
// Each thread in the block processes THREAD_TILE_SIZE_Y *
// THREAD_TILE_SIZE_X output values. Number of threads BLOCK_TILE_SIZE_Y *
// BLOCK_TILE_SIZE_X / (THREAD_TILE_SIZE_Y * THREAD_TILE_SIZE_X)
template <typename T, size_t BLOCK_TILE_SIZE_X, size_t BLOCK_TILE_SIZE_Y,
          size_t BLOCK_TILE_SIZE_K, size_t BLOCK_TILE_SKEW_SIZE_X,
          size_t BLOCK_TILE_SKEW_SIZE_Y, size_t WARP_TILE_SIZE_X,
          size_t WARP_TILE_SIZE_Y, size_t WMMA_TILE_SIZE_X,
          size_t WMMA_TILE_SIZE_Y, size_t WMMA_TILE_SIZE_K, size_t NUM_THREADS>
__global__ void gemm_v07_vectorized(size_t m, size_t n, size_t k, T alpha,
                                    T const* A, size_t lda, T const* B,
                                    size_t ldb, T beta, T* C, size_t ldc)
{
    constexpr size_t NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
    static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
    static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);

    // Cache a tile of A and B in shared memory for data reuse.
    __shared__ T A_thread_block_tile_transposed[BLOCK_TILE_SIZE_K]
                                               [BLOCK_TILE_SIZE_Y +
                                                BLOCK_TILE_SKEW_SIZE_Y];
    __shared__ T B_thread_block_tile[BLOCK_TILE_SIZE_K][BLOCK_TILE_SIZE_X +
                                                        BLOCK_TILE_SKEW_SIZE_X];

    constexpr size_t NUM_WMMA_TILES_X{WARP_TILE_SIZE_X / WMMA_TILE_SIZE_X};
    static_assert(WARP_TILE_SIZE_X % WMMA_TILE_SIZE_X == 0U);
    constexpr size_t NUM_WMMA_TILES_Y{WARP_TILE_SIZE_Y / WMMA_TILE_SIZE_Y};
    static_assert(WARP_TILE_SIZE_Y % WMMA_TILE_SIZE_Y == 0U);
    constexpr size_t NUM_WMMA_TILES_K{BLOCK_TILE_SIZE_K / WMMA_TILE_SIZE_K};
    static_assert(BLOCK_TILE_SIZE_K % WMMA_TILE_SIZE_K == 0U);

    // Declare the fragments.
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_a, WMMA_TILE_SIZE_Y,
                           WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T,
                           nvcuda::wmma::col_major>
        a_frags[NUM_WMMA_TILES_Y];
    nvcuda::wmma::fragment<nvcuda::wmma::matrix_b, WMMA_TILE_SIZE_Y,
                           WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T,
                           nvcuda::wmma::row_major>
        b_frags[NUM_WMMA_TILES_X];
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_TILE_SIZE_Y,
                           WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T>
        acc_frags[NUM_WMMA_TILES_Y][NUM_WMMA_TILES_X];
    nvcuda::wmma::fragment<nvcuda::wmma::accumulator, WMMA_TILE_SIZE_Y,
                           WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_K, T>
        c_frag;

// Make sure the accumulator starts from 0.
#pragma unroll
    for (size_t wmma_tile_row_idx{0U}; wmma_tile_row_idx < NUM_WMMA_TILES_Y;
         ++wmma_tile_row_idx)
    {
        for (size_t wmma_tile_col_idx{0U}; wmma_tile_col_idx < NUM_WMMA_TILES_X;
             ++wmma_tile_col_idx)
        {
            nvcuda::wmma::fill_fragment(
                acc_frags[wmma_tile_row_idx][wmma_tile_col_idx],
                static_cast<T>(0));
        }
    }

    size_t const thread_linear_idx{threadIdx.y * blockDim.x + threadIdx.x};
    size_t const warp_linear_idx{thread_linear_idx / 32U};
    size_t const warp_row_idx{warp_linear_idx / NUM_WARPS_X};
    size_t const warp_col_idx{warp_linear_idx % NUM_WARPS_X};

    // Number of outer loops to perform the sum of inner products.
    // C_thread_block_tile =
    // \sigma_{thread_block_tile_idx=0}^{num_thread_block_tiles-1} A[:,
    // thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
    // B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :]
    size_t const num_thread_block_tiles{(k + BLOCK_TILE_SIZE_K - 1) /
                                        BLOCK_TILE_SIZE_K};

    for (size_t thread_block_tile_idx{0U};
         thread_block_tile_idx < num_thread_block_tiles;
         ++thread_block_tile_idx)
    {
        load_data_to_shared_memory_transposed_vectorized<
            T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SIZE_K,
            NUM_THREADS, BLOCK_TILE_SKEW_SIZE_X, BLOCK_TILE_SKEW_SIZE_Y>(
            A, lda, B, ldb, A_thread_block_tile_transposed, B_thread_block_tile,
            thread_block_tile_idx, thread_linear_idx, m, n, k);
        __syncthreads();

// Perform A[:, thread_block_tile_idx:BLOCK_TILE_SIZE_K] *
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :] where A[:,
// thread_block_tile_idx:BLOCK_TILE_SIZE_K] and
// B[thread_block_tile_idx:BLOCK_TILE_SIZE_K, :] are cached in the
// shared memory as A_thread_block_tile and B_thread_block_tile,
// respectively. This inner product is further decomposed to
// BLOCK_TILE_SIZE_K outer products. A_thread_block_tile *
// B_thread_block_tile = \sigma_{k_i=0}^{BLOCK_TILE_SIZE_K-1}
// A_thread_block_tile[:, k_i] @ B_thread_block_tile[k_i, :] Note that
// both A_thread_block_tile and B_thread_block_tile can be cached in the
// register.
#pragma unroll
        for (size_t k_i{0U}; k_i < NUM_WMMA_TILES_K; ++k_i)
        {
#pragma unroll
            for (size_t wmma_tile_row_idx{0U};
                 wmma_tile_row_idx < NUM_WMMA_TILES_Y; ++wmma_tile_row_idx)
            {
                nvcuda::wmma::load_matrix_sync(
                    a_frags[wmma_tile_row_idx],
                    &A_thread_block_tile_transposed[k_i * WMMA_TILE_SIZE_K]
                                                   [warp_row_idx *
                                                        WARP_TILE_SIZE_Y +
                                                    wmma_tile_row_idx *
                                                        WMMA_TILE_SIZE_Y],
                    BLOCK_TILE_SIZE_Y + BLOCK_TILE_SKEW_SIZE_Y);
#pragma unroll
                for (size_t wmma_tile_col_idx{0U};
                     wmma_tile_col_idx < NUM_WMMA_TILES_X; ++wmma_tile_col_idx)
                {
                    // These loads are extremely slow somehow, which affects the
                    // performance a lot. Load the fragment from shared memory.
                    nvcuda::wmma::load_matrix_sync(
                        b_frags[wmma_tile_col_idx],
                        &B_thread_block_tile[k_i * WMMA_TILE_SIZE_K]
                                            [warp_col_idx * WARP_TILE_SIZE_X +
                                             wmma_tile_col_idx *
                                                 WMMA_TILE_SIZE_Y],
                        BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X);

                    // Perform the matrix multiplication.
                    nvcuda::wmma::mma_sync(
                        acc_frags[wmma_tile_row_idx][wmma_tile_col_idx],
                        a_frags[wmma_tile_row_idx], b_frags[wmma_tile_col_idx],
                        acc_frags[wmma_tile_row_idx][wmma_tile_col_idx]);
                }
            }
        }
        __syncthreads();
    }

// Write the results to DRAM.
#pragma unroll
    for (size_t wmma_tile_row_idx{0U}; wmma_tile_row_idx < NUM_WMMA_TILES_Y;
         ++wmma_tile_row_idx)
    {
#pragma unroll
        for (size_t wmma_tile_col_idx{0U}; wmma_tile_col_idx < NUM_WMMA_TILES_X;
             ++wmma_tile_col_idx)
        {
            // Load the fragment from shared memory.
            nvcuda::wmma::load_matrix_sync(
                c_frag,
                &C[(blockIdx.y * BLOCK_TILE_SIZE_Y +
                    warp_row_idx * WARP_TILE_SIZE_Y +
                    wmma_tile_row_idx * WMMA_TILE_SIZE_Y) *
                       n +
                   blockIdx.x * BLOCK_TILE_SIZE_X +
                   warp_col_idx * WARP_TILE_SIZE_X +
                   wmma_tile_col_idx * WMMA_TILE_SIZE_X],
                n, nvcuda::wmma::mem_row_major);
            // Perform scaling and addition.
            for (size_t i{0}; i < c_frag.num_elements; ++i)
            {
                c_frag.x[i] =
                    alpha *
                        acc_frags[wmma_tile_row_idx][wmma_tile_col_idx].x[i] +
                    beta * c_frag.x[i];
            }
            // Store the fragment back to shared memory.
            nvcuda::wmma::store_matrix_sync(
                &C[(blockIdx.y * BLOCK_TILE_SIZE_Y +
                    warp_row_idx * WARP_TILE_SIZE_Y +
                    wmma_tile_row_idx * WMMA_TILE_SIZE_Y) *
                       n +
                   blockIdx.x * BLOCK_TILE_SIZE_X +
                   warp_col_idx * WARP_TILE_SIZE_X +
                   wmma_tile_col_idx * WMMA_TILE_SIZE_X],
                c_frag, n, nvcuda::wmma::mem_row_major);
        }
    }
}

template <typename T>
void launch_gemm_kernel_v07_vectorized(size_t m, size_t n, size_t k,
                                       T const* alpha, T const* A, size_t lda,
                                       T const* B, size_t ldb, T const* beta,
                                       T* C, size_t ldc, cudaStream_t stream)
{
    // Feel free to play with the block tile sizes.
    // The algorithm correctness should always be guaranteed.
    constexpr unsigned int BLOCK_TILE_SIZE_X{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_Y{128U};
    constexpr unsigned int BLOCK_TILE_SIZE_K{16U};

    // The skew size is used to avoid bank conflicts in shared memory.
    constexpr size_t BLOCK_TILE_SKEW_SIZE_X{16U};
    constexpr size_t BLOCK_TILE_SKEW_SIZE_Y{16U};

    constexpr unsigned int WARP_TILE_SIZE_X{32U};
    constexpr unsigned int WARP_TILE_SIZE_Y{64U};
    constexpr unsigned int NUM_WARPS_X{BLOCK_TILE_SIZE_X / WARP_TILE_SIZE_X};
    constexpr unsigned int NUM_WARPS_Y{BLOCK_TILE_SIZE_Y / WARP_TILE_SIZE_Y};
    static_assert(BLOCK_TILE_SIZE_X % WARP_TILE_SIZE_X == 0U);
    static_assert(BLOCK_TILE_SIZE_Y % WARP_TILE_SIZE_Y == 0U);

    constexpr unsigned int WMMA_TILE_SIZE_X{16U};
    constexpr unsigned int WMMA_TILE_SIZE_Y{16U};
    constexpr unsigned int WMMA_TILE_SIZE_K{16U};

    constexpr unsigned int NUM_THREADS_PER_BLOCK{NUM_WARPS_X * NUM_WARPS_Y *
                                                 32U};

    dim3 const block_dim{NUM_THREADS_PER_BLOCK, 1U, 1U};
    dim3 const grid_dim{
        (static_cast<unsigned int>(n) + BLOCK_TILE_SIZE_X - 1U) /
            BLOCK_TILE_SIZE_X,
        (static_cast<unsigned int>(m) + BLOCK_TILE_SIZE_Y - 1U) /
            BLOCK_TILE_SIZE_Y,
        1U};
    gemm_v07_vectorized<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y,
                        BLOCK_TILE_SIZE_K, BLOCK_TILE_SKEW_SIZE_X,
                        BLOCK_TILE_SKEW_SIZE_Y, WARP_TILE_SIZE_X,
                        WARP_TILE_SIZE_Y, WMMA_TILE_SIZE_X, WMMA_TILE_SIZE_Y,
                        WMMA_TILE_SIZE_K, NUM_THREADS_PER_BLOCK>
        <<<grid_dim, block_dim, 0U, stream>>>(m, n, k, *alpha, A, lda, B, ldb,
                                              *beta, C, ldc);
    CHECK_LAST_CUDA_ERROR();
}

Because the fundamental WMMA size is $16 \times 16 \times 16$, all the 32 threads in the same warp has to synergistically access the shared memory where the WMMA fragment is cached. It is then very possible that the shared memory bank conflicts will happen. To avoid the shared memory bank conflicts, we will have to pad the shared memory size to make sure the shared memory bank conflicts will not happen. This is why we have to use the skew size to pad the shared memory size at the leading dimension.

The performance of this FP16 GEMM implementation becomes 46.78 TFLOPS on an NVIDIA GeForce RTX 3090 GPU. Comparing to the cuBLAS FP16 GEMM performance, which is 138.95 TFLOPS, this implementation only achieves 33.7% of the cuBLAS FP16 GEMM performance. We will leave the performance optimization of this implementation as a future work.

Conclusions

The optimizations we performed on the GEMM CUDA kernels mainly follow the diagrams in the article “CUTLASS: Fast Linear Algebra in CUDA C++”.

The Complete GEMM CUDA Kernel Hierarchy

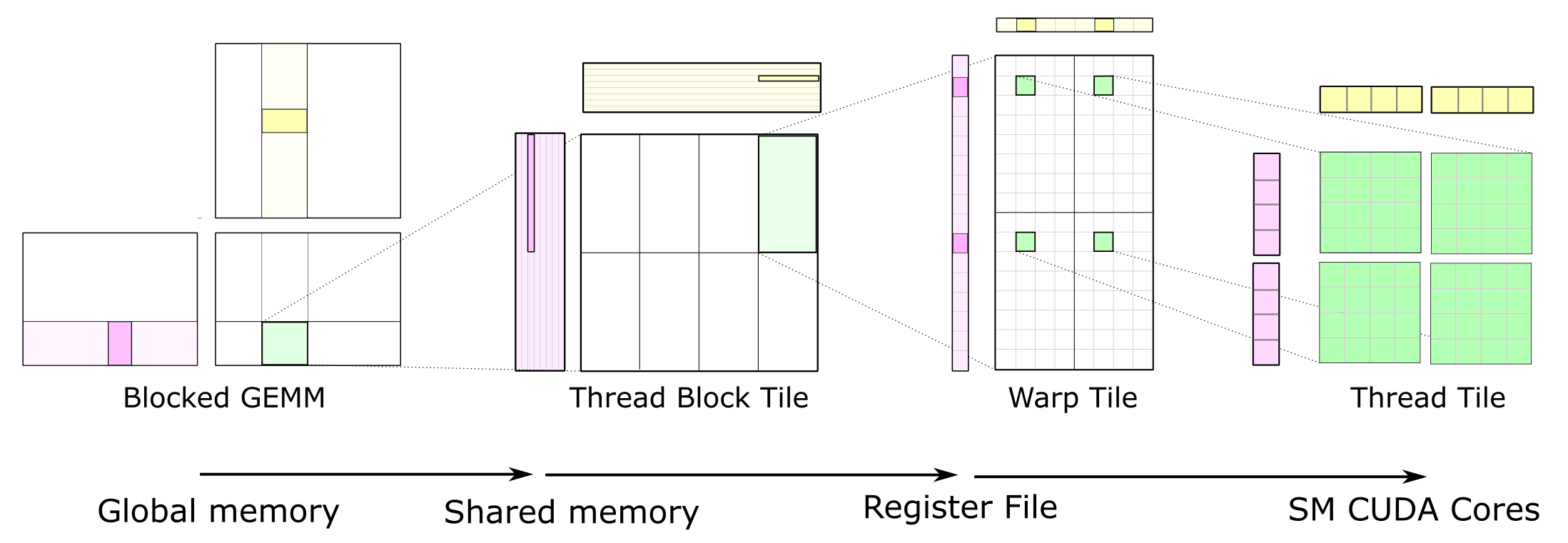
With the optimization techniques, such as 2D block tiling, 2D warp tiling, 2D thread tiling, and vectorized memory access, we can achieve 20.16 TFLOPS FP32 GEMM performance on an NVIDIA GeForce RTX 3090 GPU, which is 80% - 90% of the cuBLAS FP32 GEMM performance.

Source Code

The source code of the GEMM CUDA kernels can be found in my GitHub repository “CUDA GEMM Optimization”.

References

CUDA Matrix Multiplication Optimization

https://leimao.github.io/article/CUDA-Matrix-Multiplication-Optimization/

Author

Lei Mao

Posted on

01-20-2024

Updated on

01-20-2024

Licensed under

 

Like this article? Support the author with

Comments

  Follow   Sponsor

Advertisement


×