Number of Alignments in Connectionist Temporal Classification (CTC)

Introduction

In some sequence modeling problems, the length of labels is shorter than the length of outputs. For example, in speech recognition, given an audio clip, the model would predict a sequence of tokens. But the sequence length of the transcript is often shorter than the sequence of the predicted tokens. These sequence modeling problems are different from classical classification sequence modeling problems where each predicted token has an unambiguous label and could be modeled as Connectionist Temporal Classification (CTC) problems. The CTC loss could be employed for training the model accordingly.

The article “Sequence Modeling With CTC” on Distill described the CTC very well. I am not sure if I could write a better article on CTC compared to it, so a good idea is not to do so. However, there is an interesting mathematical statement in the article that is not well justified. So in this blog post, I would go over the CTC process at a super high level, then I would discuss the interesting mathematical statement for CTC described in the “Sequence Modeling With CTC”. To understand more details on CTC, the readers should refer to the “Sequence Modeling With CTC” on Distill.

Overview of Connectionist Temporal Classification

In CTC classification, we have a special token $\epsilon$ in the vocabulary. Given an input sequence, we predict all the probability vectors for each of the token positions in the predicted sequence from the model. Each possible predicted token sequence would have a probability by computing the product of the probability of each token in the predicted sequence. Each possible predicted token sequence could be further reduced by first merging the same consecutive tokens, followed by the removal of $\epsilon$.

For example, a predicted token sequence [h, e, l, l, $\epsilon$, l, l, o, o] would be reduced to sequence [h, e, l, l, o], a predicted token sequence [h, e, l, l, l, l, $\epsilon$, o, o] would be reduced to sequence [h, e, l, o], a predicted token sequence [h, e, l, $\epsilon$, l, l, l, o, o] would also be reduced to sequence [h, e, l, l, o].

As you have probably found out, the predicted token sequence corresponding to a certain reduced sequence is not unique. Instead of being a one-to-one mapping, it is a many-to-one mapping.

Given the label sequence for the input sequence, we would need to find out all the predicted token sequence which could be reduced to the label sequence, compute their probability, and sum them up as the marginalized probability for the label sequence. During training, we would like to maximize the marginalized probability for the label sequence.

The number of the predicted token sequence which could be reduced to the label sequence could be huge, thus it could be intractable to compute the marginalized probability. Fortunately, with the help of dynamic programming, the computation cost is asymptotically reduced.

Number of Alignments in Connectionist Temporal Classification

The number of the predicted token sequence which could be reduced to the label sequence could be huge thus it could be intractable to compute the marginalized probability.

In the “Sequence Modeling With CTC”, there is an interesting mathematical statement with some modification from me. For a $Y$ of length $U$ without any repeat characters and $X$ of length $T$, assuming $T \geq U$, the number of CTC alignments (the number of different $X$s) is ${T + U \choose T - U}$. Here, $Y$ is the label sequence, and $X$ is any predicted token sequence.

Probably because I did not read as many papers as the author of the “Sequence Modeling With CTC” has read on CTC, I was not able to find the proof to this from the literature. Because it is an interesting statement, I would like to prove it by myself.

To be honest, if I did not know the number of CTC alignment is ${T + U \choose T - U}$, I might have difficulty in deriving this. However, to prove the number of CTC alignment is ${T + U \choose T - U}$, it is somewhat easier, but still tricky.

Given $X$ of length $T$ and $Y$ of length $U$, we prepare an empty sequence $Z$ of length $T + U$. Because $T \geq U$ and $T + U \geq 2U$, we could always select $2U$ tokens from the sequence $Z$, and the number of the combinations is ${T + U \choose 2U } = {T + U \choose T - U }$.

The $2U$ tokens are for the all the tokens from $Y$, and the last tokens in $X$ corresponding to the tokens in $Y$. We call the last tokens in $X$ corresponding to the tokens in $Y$ as $Y^\prime$. Starting with the tokens in $Y$, we iteratively put the tokens from $Y$ and $Y^\prime$ to the $2U$ tokens. This might sound a little bit vague, let’s see an example.

We have $Y = \{a,b\}$ of length $U=2$. We also have $X$ of length $T=7$. Therefore, $Z$ has length of $U+T=9$. An example of the placement of the 2U would in $Z$ would be:

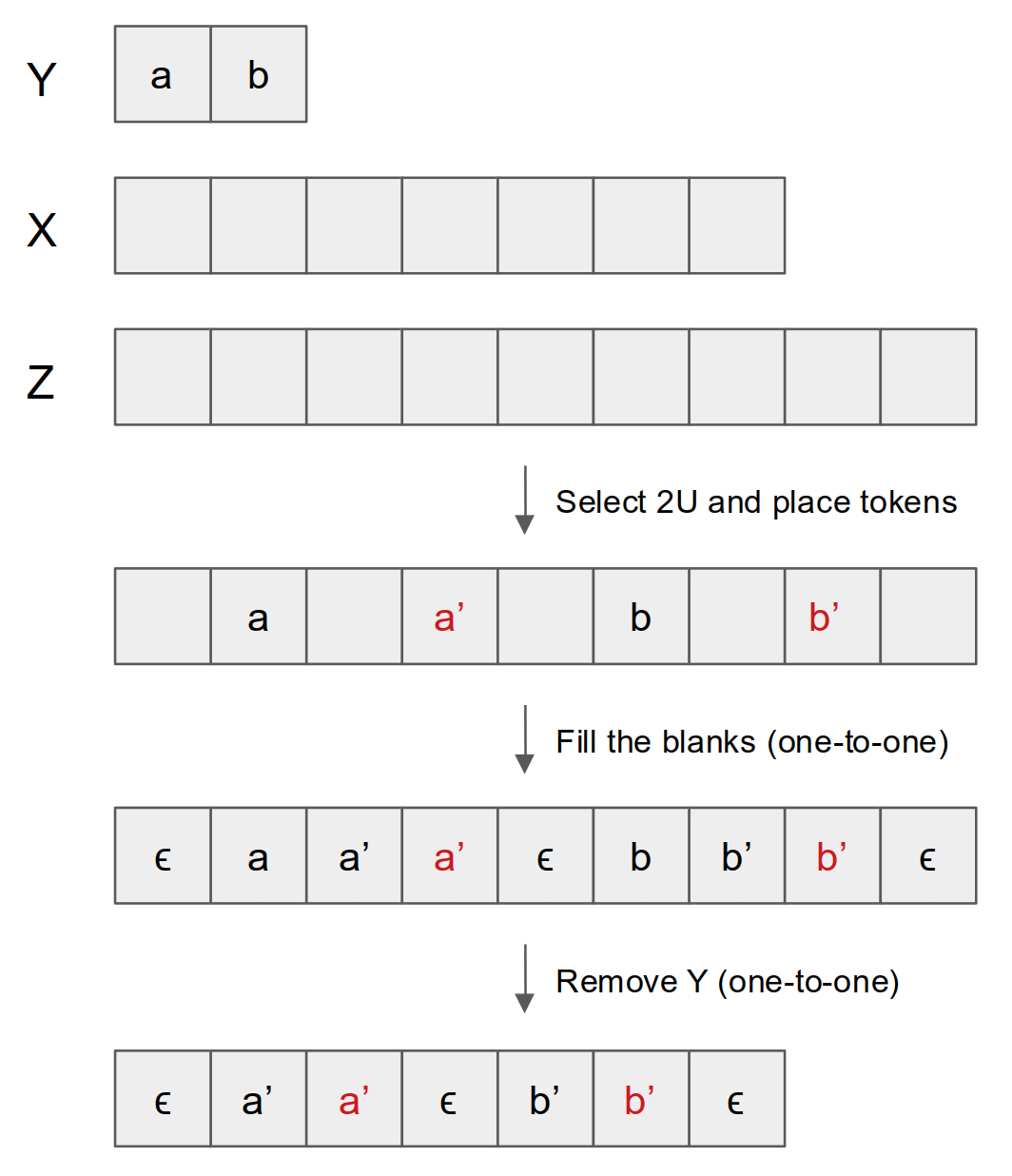
We then fill the blanks. The rule is in $Z$ the token before the last corresponding token and after previous token from $Y$ are the same as the last corresponding token. The rest of the tokens are just filled with $\epsilon$. This is a one-to-one projection.

The next step is simply to remove the tokens from $Y$ in $Z$. This is a one-to-one projection.

By this means, each combination of $2U$ tokens from the $T + U$ tokens will be a valid, one-to-one correspondent CTC alignment. Because we have ${T + U\choose2U} = {T + U \choose T - U}$ combinations in total, so we have ${T + U\choose2U} = {T + U \choose T - U}$ CTC alignments.

This concludes the proof.

We could see that the number of CTC alignment could be very large, even for small $U$ and $T$s. Therefore, we need to use dynamic programming to compute the probability of the label asymptotically faster.

References

• Sequence Modeling With CTC