Camera Frustum Space
Introduction
The camera frustum space is a 3D space defined by the camera frustum. It has one additional depth dimension comparing to the 2D camera image space. This additional depth dimension is useful for encoding the information such as the feature matching cost for determining the depth of a pixel.
In this blog post, I would like to discuss the mapping from the camera frustum space to the camera space and the 3D world space.
Camera Frustum
The camera frustum space was first introduced in the DSGN paper. The camera frustum space is a 3D space defined by the camera frustum.

There is a one-to-one mapping between the camera frustum space and the 3D world space.
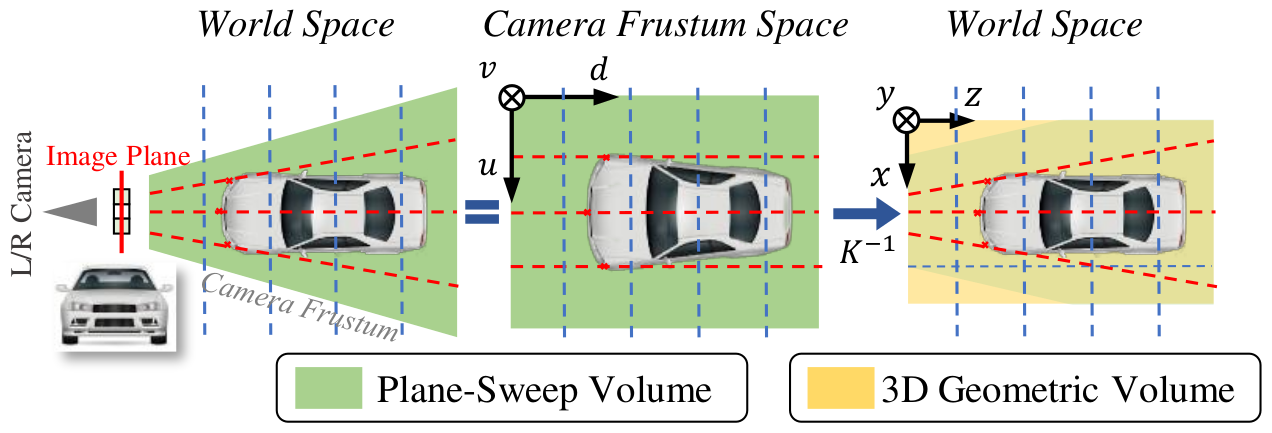
In the next sections, we will derive the mathematics for the from the 3D world space to the camera frustum space and vice versa.
Camera Frustum Space To Camera Space
For each ray to the camera pinhole, each point on the ray with different depth maps to the same point on the image plane. This many-to-one mapping can be computed using camera intrinsic matrix. Concretely, for a 3D camera-centered point $\mathbf{p}^{\text{3D}}_c = [x_c, y_c, z_c]^{\top}$ in the 3D camera space, the corresponding 2D image point $\mathbf{p}^{\text{2D}} = (u, v)$ can be computed as follows:
$$
\begin{align}
\tilde{\mathbf{p}}^{\text{2D}} &= \mathbf{K} \mathbf{p}^{\text{3D}}_c \\
&=
d
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} \\
&=
\begin{bmatrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
\end{bmatrix}
\\
\end{align}
$$
where $\mathbf{K}$ is the camera intrinsic matrix, $d$ is the depth because $d = z_c$, $f_x$ and $f_y$ are the focal lengths, and $c_x$ and $c_y$ denotes the optical center.
The depth $d$ is not useful in the mapping from the 3D camera space to the 2D camera image space. However, it is useful in the mapping from the camera frustum space to the 3D camera space. The camera frustum space is just the 2D camera image space augmented with the depth. Concretely, for a 2D image point $\mathbf{p}^{\text{2D}} = (u, v)$, it has infinite number of correspondent points $(u, v, d)$ in the camera frustum space with different depth $d$, the corresponding 3D camera-centered point $\mathbf{p}^{\text{3D}}_c = [x_c, y_c, z_c]^{\top}$ can be computed as follows:
$$
\begin{align}
\mathbf{p}^{\text{3D}}_c &= \mathbf{K}^{-1} \tilde{\mathbf{p}}^{\text{2D}} \\
&=
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
\end{bmatrix} \\
&=
\begin{bmatrix}
f_x & 0 & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{bmatrix}^{-1}
d
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix}
\\
&=
\begin{bmatrix}
\frac{1}{f_x} & 0 & -\frac{c_x}{f_x} \\
0 & \frac{1}{f_y} & -\frac{c_y}{f_y} \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
ud \\
vd \\
d
\end{bmatrix}
\\
\end{align}
$$
where $\mathbf{K}^{-1}$ is the inverse of the camera intrinsic matrix.
Camera Frustum Space To 3D World Space
In practice, the 3D point is not camera-centered in the 3D camera space, but in the 3D world space. The 3D point in the 3D camera space can be related with the 3D point in the 3D world space using the camera extrinsic matrix. Concretely, for a 3D world-centered point $\mathbf{p}^{\text{3D}}_w = [x, y, z]^{\top}$ in the 3D world space, the corresponding 3D camera-centered point $\mathbf{p}^{\text{3D}}_c = [x_c, y_c, z_c]^{\top}$ in the 3D camera space can be computed as follows:
$$
\begin{align}
\mathbf{p}^{\text{3D}}_c &= \left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ]\bar{\mathbf{p}}^{\text{3D}}_w \\
&=
\begin{bmatrix}
x_c \\
y_c \\
z_c \\
\end{bmatrix} \\
&=
\begin{bmatrix}
R_{1,1} & R_{1,2} & R_{1,3} & t_x \\
R_{2,1} & R_{2,2} & R_{2,3} & t_y \\
R_{3,1} & R_{3,2} & R_{3,3} & t_z \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1 \\
\end{bmatrix}
\\
&=
\begin{bmatrix}
R_{1,1} & R_{1,2} & R_{1,3} \\
R_{2,1} & R_{2,2} & R_{2,3} \\
R_{3,1} & R_{3,2} & R_{3,3} \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
+
\begin{bmatrix}
t_x \\
t_y \\
t_z \\
\end{bmatrix}
\end{align}
$$
where $\mathbf{R}$ is the rotation matrix and $\mathbf{t}$ is the translation vector in the camera extrinsic matrix.
The 2D image point $\mathbf{p}^{\text{2D}} = (u, v)$ can be related with the 3D point in the 3D world space $\mathbf{p}^{\text{3D}}_w = [x, y, z]^{\top}$ using the camera extrinsic matrix and the camera intrinsic matrix. Concretely, for a 3D world-centered point $\mathbf{p}^{\text{3D}}_w = [x, y, z]^{\top}$ in the 3D world space, the corresponding 2D image point $\mathbf{p}^{\text{2D}} = (u, v)$ can be computed as follows:
$$
\begin{align}
\tilde{\mathbf{p}}^{\text{2D}} &=
\mathbf{K}
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ]
\bar{\mathbf{p}}^{\text{3D}}_w \\
&=
d
\begin{bmatrix}
u \\
v \\
1
\end{bmatrix} \\
&=
\mathbf{K}
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ]
\begin{bmatrix}
x \\
y \\
z \\
1 \\
\end{bmatrix}
\end{align}
$$
It is more convenient to use a $4 \times 4$ square invertible camera matrix $\tilde{\mathbf{P}} \in \mathbb{R}^{4 \times 4}$ so that the mapping from the camera frustum space to the 3D world space can be represented as a single matrix multiplication. The camera matrix $\tilde{\mathbf{P}}$ is defined as
$$
\tilde{\mathbf{P}} =
\left [
\begin{array}{c|c}
\mathbf{K} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
$$
Given a 3D world-centered point $\mathbf{p}^{\text{3D}}_w = [x, y, z]^{\top}$ in the 3D world space, the corresponding 2D image point $\mathbf{p}^{\text{2D}} = (u, v)$ can be computed as follows:
$$
\begin{align}
\left [
\begin{array}{c|c}
\tilde{\mathbf{p}}^{\text{2D}} \\
\hline
1 \\
\end{array}
\right ]
&=
\tilde{\mathbf{P}}
\bar{\mathbf{p}}^{\text{3D}}_w
\\
&=
\begin{bmatrix}
ud \\
vd \\
d \\
1 \\
\end{bmatrix}
\\
&=
\left [
\begin{array}{c|c}
\mathbf{K} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\begin{bmatrix}
x \\
y \\
z \\
1 \\
\end{bmatrix}
\end{align}
$$
The inverse of the camera matrix $\tilde{\mathbf{P}}$ is
$$
\tilde{\mathbf{P}}^{-1} =
\left [
\begin{array}{c|c}
\mathbf{R}^{-1} & -\mathbf{R}^{-1}\mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{K}^{-1} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
$$
where $\mathbf{R}^{-1}$ is the inverse of the rotation matrix $\mathbf{R}$ and
$$
\begin{align}
\mathbf{R}^{-1} &=
\begin{bmatrix}
R_{1,1} & R_{2,1} & R_{3,1} \\
R_{1,2} & R_{2,2} & R_{3,2} \\
R_{1,3} & R_{2,3} & R_{3,3} \\
\end{bmatrix}^{-1} \\
&=
\begin{bmatrix}
R_{1,1} & R_{1,2} & R_{1,3} \\
R_{2,1} & R_{2,2} & R_{2,3} \\
R_{3,1} & R_{3,2} & R_{3,3} \\
\end{bmatrix}
\end{align}
$$
Therefore, given a point $(u, v, d)$ from the camera frustum space, the corresponding 3D world-centered point $\mathbf{p}^{\text{3D}}_w = [x, y, z]^{\top}$ can be computed as follows:
$$
\begin{align}
\bar{\mathbf{p}}^{\text{3D}}_w
&=
\tilde{\mathbf{P}}^{-1}
\left [
\begin{array}{c|c}
\tilde{\mathbf{p}}^{\text{2D}} \\
\hline
1 \\
\end{array}
\right ]
\\
&=
\begin{bmatrix}
x \\
y \\
z \\
1 \\
\end{bmatrix} \\
&=
\left [
\begin{array}{c|c}
\mathbf{R}^{-1} & -\mathbf{R}^{-1}\mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{K}^{-1} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\tilde{\mathbf{p}}^{\text{2D}} \\
\hline
1 \\
\end{array}
\right ]
\\
&=
\left [
\begin{array}{c|c}
\mathbf{R}^{-1} & -\mathbf{R}^{-1}\mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{K}^{-1} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\begin{bmatrix}
ud \\
vd \\
d \\
1 \\
\end{bmatrix}
\\
\end{align}
$$
Conclusions
The camera frustum space is just the 2D camera image space with an additional depth dimension. The camera frustum space can be mapped to the 3D world space using the camera intrinsic matrix and the camera extrinsic matrix. This mapping is just the inverse mapping from the 3D world space to the camera 2D space.
References
Camera Frustum Space