Camera Intrinsics and Extrinsics
Introduction
Camera projects a 3D point in real world to a 2D point on image, and this transformation is actually a matrix multiplication.
In this blog post, I would like to discuss the mathematics on camera projection, camera matrix, camera intrinsic matrix, and camera extrinsic matrix.
Camera Intrinsics
The camera intrinsic matrix maps a 3D camera-centered point to a 2D homogeneous point on the image plane.
Camera Intrinsic Matrix
The camera intrinsic matrix $\mathbf{K} \in \mathbb{R}^{3 \times 3}$ is an upper triangular matrix defined as
$$
\mathbf{K} =
\begin{bmatrix}
f_x & s & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{bmatrix}
$$
where
$f_x$ and $f_y$ are the focal length for the sensor at the $x$ and $y$ dimensions, respectively, in unit of pixels;
$s$ any possible skew between the sensor axes due to the sensor not being mounted perpendicular to the optical axis, usually $s = 0$ unless the sensor axis and the optical axis are not aligned;
$c_x$ and $c_y$ denotes the optical center expressed in pixel coordinates, in unit of pixels.
The camera intrinsic matrix operates on a 3D camera-centered point $\mathbf{p}_c = [X, Y, Z]^{\top}$ in any unit and results in a 2D homogeneous point $\tilde{\mathbf{x}}_s = [\tilde{x}_s, \tilde{y}_s, \tilde{w}_s]^{\top} = \tilde{w}_s [x_s, y_s, 1]^{\top}$ on the image plane in unit of pixels. That is to say,
$$
\tilde{\mathbf{x}}_s = \mathbf{K} \mathbf{p}_c
$$
It should be noted that $\mathbf{p}_c$ is the 3D coordinates using the camera intrinsic reference frame, instead of the real world reference frame. The mapping from the real world reference frame to the camera intrinsic reference frame will be conducted by camera extrinsic matrix.
Camera Intrinsic Matrix Decomposition
The camera intrinsic matrix could be decomposed into three matrices.
$$
\begin{align}
\mathbf{K}
&=
\begin{bmatrix}
f_x & s & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{bmatrix} \\
&=
\underbrace{
\begin{bmatrix}
1 & 0 & c_x \\
0 & 1 & c_y \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Translation}}
\underbrace{
\begin{bmatrix}
f_x & 0 & 0 \\
0 & f_y & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Scaling}}
\underbrace{
\begin{bmatrix}
1 & \frac{s}{f_x} & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Shear}}
\\
&=
\underbrace{
\begin{bmatrix}
1 & 0 & c_x \\
0 & 1 & c_y \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Translation}}
\underbrace{
\begin{bmatrix}
1 & \frac{s}{f_y} & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Shear}}
\underbrace{
\begin{bmatrix}
f_x & 0 & 0 \\
0 & f_y & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Scaling}}
\\
\end{align}
$$
The camera 2D scaling matrix is probably the most confusing one. Assuming $f = f_x = f_y$, $c_x = c_y = 0$ (no 2D translation), and $s = 0$ (no 2D shear), let’s apply the 2D scaling matrix to the 3D camera-centered point $\mathbf{p}_c = [X, Y, Z]^{\top}$.
$$
\begin{align}
\tilde{\mathbf{x}}_s
&=
\mathbf{K} \mathbf{p}_c
\\
&=
\begin{bmatrix}
f_x & s & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
Z \\
\end{bmatrix}
\\
&=
\underbrace{
\begin{bmatrix}
1 & 0 & c_x \\
0 & 1 & c_y \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Translation}}
\underbrace{
\begin{bmatrix}
f_x & 0 & 0 \\
0 & f_y & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Scaling}}
\underbrace{
\begin{bmatrix}
1 & \frac{s}{f_x} & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Shear}}
\begin{bmatrix}
X \\
Y \\
Z \\
\end{bmatrix}
\\
&=
\underbrace{
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Translation}}
\underbrace{
\begin{bmatrix}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Scaling}}
\underbrace{
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Shear}}
\begin{bmatrix}
X \\
Y \\
Z \\
\end{bmatrix}
\\
&=
\underbrace{
\begin{bmatrix}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
}_{\text{2D Scaling}}
\begin{bmatrix}
X \\
Y \\
Z \\
\end{bmatrix}
\\
&=
\begin{bmatrix}
fX \\
fY \\
Z \\
\end{bmatrix}
\\
&=
Z
\begin{bmatrix}
f\frac{X}{Z} \\
f\frac{Y}{Z} \\
1 \\
\end{bmatrix}
\\
\end{align}
$$
The following figure is the geometry of mapping 3D points $(X, Y, Z)$ to 2D points $(x, y)$ on image.
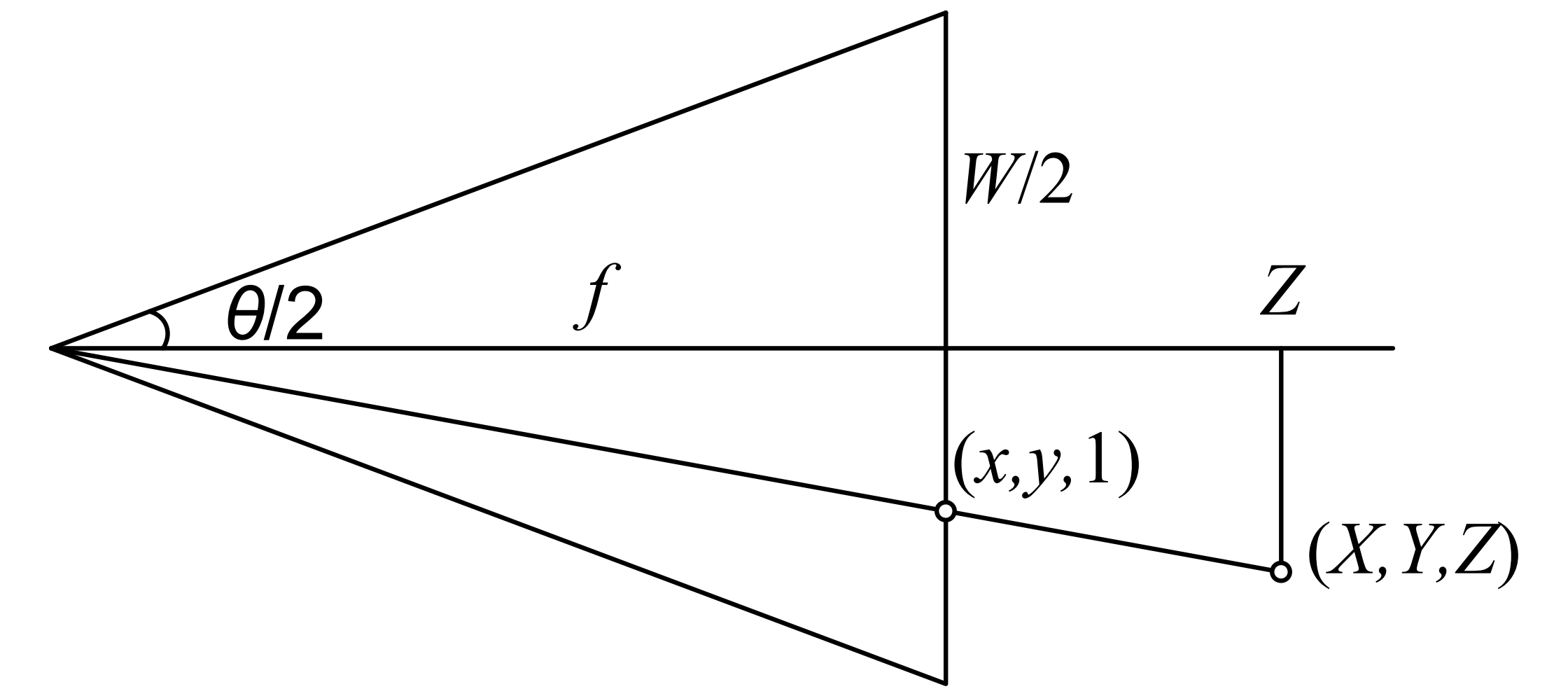
Because of the property of similar triangles, it is not difficult to find that
$$
\begin{align}
x &= f\frac{X}{Z} \\
y &= f\frac{Y}{Z} \\
\end{align}
$$
This verifies that the camera intrinsic matrix maps a 3D camera-centered point to a 2D homogeneous point on the image plane.
More commonly, the optical center located at the center of the sensor and $c_x = c_y \neq 0$.
$$
\begin{align}
\tilde{\mathbf{x}}_s
&=
\mathbf{K} \mathbf{p}_c
\\
&=
\begin{bmatrix}
fX + c_x Z \\
fY + c_y Z \\
Z \\
\end{bmatrix}
\\
&=
Z
\begin{bmatrix}
f\frac{X}{Z} + c_x \\
f\frac{Y}{Z} + c_x \\
1 \\
\end{bmatrix}
\end{align}
$$
The camera intrinsic mapping still makes sense.
All the parameters of the camera intrinsic matrix are from the camera itself. That’s why the matrix is called the intrinsic matrix.
Other Camera Intrinsic Geometric Transformations
There are other camera intrinsic geometric transformations, such as sensor rotation. In principle, we will have to apply a 3D rotation matrix $\mathbf{R} \in \mathbb{R}^{3 \times 3}$ and possibly another 3D translation in the camera intrinsic matrix so that the new camera intrinsic matrix could be something like $\mathbf{K} [ \mathbf{R} | \mathbf{t} ]$. However, sensor ration is just equivalent as camera rotation and the rotation matrix could be merged into the camera extrinsic matrix.
Camera Extrinsics
In the previous sections, we have learned how to use the camera intrinsic matrix maps a 3D camera-centered point to a 2D homogeneous point on the image plane. The 3D point in the real world is usually not camera-centered. So we will have to use the camera extrinsic matrix maps a 3D world-centered point to a 3D camera-centered point.
Camera Extrinsic Matrix
The camera extrinsic matrix basically converts the 3D point coordinates from the world-arbitrary reference frame to the camera reference frame and does only 3D rotation and translation. The expression is thus much simpler.
The camera extrinsic matrix $[ \mathbf{R} | \mathbf{t} ] \in \mathbb{R}^{3 \times 4}$ is defined as
$$
\begin{align}
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ] &=
\left[ \begin{array}{ccc|c}
R_{1,1} & R_{1,2} & R_{1,3} & t_0 \\
R_{2,1} & R_{2,2} & R_{2,3} & t_1 \\
R_{3,1} & R_{3,2} & R_{3,3} & t_2 \\
\end{array} \right]
\end{align}
$$
Not surprisingly it is a rotation and translation matrix.
The camera intrinsic matrix operates on a 3D world-centered augmented point $\bar{\mathbf{p}}_w = [X^{\prime}, Y^{\prime}, Z^{\prime}, 1]^{\top}$ in any unit and results in a 3D camera-centered point $\mathbf{p}_c = [X, Y, Z]^{\top}$. That is to say,
$$
\mathbf{p}_c =
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ] \bar{\mathbf{p}}_w
$$
Camera Extrinsic Matrix Decomposition
The camera extrinsic matrix $[ \mathbf{R} | \mathbf{t} ] \in \mathbb{R}^{3 \times 4}$ could be decomposed into a rotation matrix and a translational matrix.
$$
\begin{align}
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ]
&=
\underbrace{
\left [
\begin{array}{c|c}
\mathbf{I} & \mathbf{t} \\
\end{array}
\right ]
}_{\text{3D Translation}}
\underbrace{
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
}_{\text{3D Rotation}}
\\
&=
\underbrace{
\begin{bmatrix}
1 & 0 & 0 & t_1 \\
0 & 1 & 0 & t_2 \\
0 & 0 & 1 & t_3 \\
\end{bmatrix}
}_{\text{3D Translation}}
\underbrace{
\begin{bmatrix}
R_{1,1} & R_{1,2} & R_{1,3} & 0 \\
R_{2,1} & R_{2,2} & R_{2,3} & 0 \\
R_{3,1} & R_{3,2} & R_{3,3} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
}_{\text{3D Rotation}}
\end{align}
$$
3D World to 2D Image Mapping
The 3D world augmented coordinates $\bar{\mathbf{p}}_w = [X^{\prime}, Y^{\prime}, Z^{\prime}, 1]^{\top}$ to 2D image pixel homogeneous coordinates 2D homogeneous point $\tilde{\mathbf{x}}_s = [\tilde{x}_s, \tilde{y}_s, \tilde{w}_s]^{\top} = \tilde{w}_s [x_s, y_s, 1]^{\top}$ is just applying the camera extrinsic matrix $[ \mathbf{R} | \mathbf{t} ] \in \mathbb{R}^{3 \times 4}$ followed by the camera intrinsic matrix $\mathbf{K} \in \mathbb{R}^{3 \times 3}$ onto the 3D world coordinates.
$$
\begin{align}
\tilde{\mathbf{x}}_s &=
\mathbf{K}
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ]
\bar{\mathbf{p}}_w
\end{align}
$$
Camera Matrix
The camera extrinsic matrix $[ \mathbf{R} | \mathbf{t} ] \in \mathbb{R}^{3 \times 4}$ and the camera intrinsic matrix $\mathbf{K} \in \mathbb{R}^{3 \times 3}$ could be combined into one single matrix called camera matrix $\mathbf{P} \in \mathbb{R}^{3 \times 4}$.
$$
\mathbf{P} = \mathbf{K}
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\end{array}
\right ]
$$
Therefore,
$$
\begin{align}
\tilde{\mathbf{x}}_s &=
\mathbf{P}
\bar{\mathbf{p}}_w
\end{align}
$$
Sometimes, it is preferable to use a $4 \times 4$ square invertible camera matrix $\tilde{\mathbf{P}} \in \mathbb{R}^{4 \times 4}$ and $\tilde{\mathbf{P}}$ is defined as
$$
\tilde{\mathbf{P}} =
\left [
\begin{array}{c|c}
\mathbf{K} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
$$
Let’s check what $\tilde{\mathbf{x}}_s^{\prime} = \tilde{\mathbf{P}} \bar{\mathbf{p}}_w$ gives us.
$$
\begin{align}
\tilde{\mathbf{x}}_s^{\prime} &=
\tilde{\mathbf{P}}
\bar{\mathbf{p}}_w
\\
&=
\left [
\begin{array}{c|c}
\mathbf{K} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{R} & \mathbf{t} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\bar{\mathbf{p}}_w
\\
&=
\left [
\begin{array}{c|c}
\mathbf{K} & \mathbf{0}^{\top} \\
\hline
\mathbf{0} & 1 \\
\end{array}
\right ]
\left [
\begin{array}{c|c}
\mathbf{p}_c \\
1 \\
\end{array}
\right ]
\\
&=
\left [
\begin{array}{c|c}
\mathbf{K} \mathbf{p}_c \\
1 \\
\end{array}
\right ]
\\
&=
\left [
\begin{array}{c|c}
\tilde{\mathbf{x}}_s \\
1 \\
\end{array}
\right ]
\\
&=
\left [
\begin{array}{c|c}
\tilde{\mathbf{x}}_s \\
1 \\
\end{array}
\right ]
\\
&=
\left [
\begin{array}{c|c}
\tilde{x}_s \\
\tilde{y}_s \\
\tilde{w}_s \\
1 \\
\end{array}
\right ]
\\
&=
\tilde{w}_s
\left [
\begin{array}{c|c}
x_s \\
y_s \\
1 \\
\frac{1}{\tilde{w}_s} \\
\end{array}
\right ]
\\
&\sim
\left [
\begin{array}{c|c}
x_s \\
y_s \\
1 \\
\frac{1}{\tilde{w}_s} \\
\end{array}
\right ]
\\
&=
\left [
\begin{array}{c|c}
x_s \\
y_s \\
1 \\
d \\
\end{array}
\right ]
\\
\end{align}
$$
where we define $d = \frac{1}{\tilde{w}_s}$.
Notice from our derivation previously, $\tilde{w}_s = Z$. Therefore, $d = \frac{1}{Z}$ and $d$ is called inverse depth.
Calibration
Getting the parameters for the camera intrinsic matrix and the camera extrinsic matrix is called calibration. We will discuss the extrinsic calibration and camera (intrinsic) calibration later.
References
Camera Intrinsics and Extrinsics