Number of Parameters for Causal Inference

Introduction

Without knowing the structure of the probabilistic graphical model and some rigorous assumption about the relationships between the random variables, the number of parameters required to represent the probabilistic graphical model is usually intractable.

In this blog post, I would like to show how to reduce the number of parameters required to represent the probabilistic graphical model by posing assumptions.

Probabilistic Graphical Model

Suppose we have $n$ binary variables, $X_1, X_2, \cdots, X_n$, and we would like to build a model to compute the joint distribution $P(X_1, X_2, \cdots, X_n)$.

Chain Rule

If we have no prior knowledge about the structure of random variables in a Bayesian network, to compute a joint distribution, we have to use probabilistic chain rule. One of the ways to factorize $P(X_1, X_2, \cdots, X_n)$ using the chain rule is

$$
\begin{align}
P(X_1, X_2, \cdots, X_n) &= P(X_1) P(X_2 | X_1) P(X_3 | X_1, X_2) \cdots P(X_n | X_1, X_2, \cdots, X_{n-1}) \\
&= P(X_1) \prod_{i=2}^{n} P(X_i | X_1, \cdots, X_{i-1})
\end{align}
$$

Let’s compute how many parameters are required for this model. Because $X_i$ is a binary variable, $P(X_i)$ requires exactly one parameter. For example,

$$
\begin{align}
P(X_i = 1) &= \lambda_i \\
P(X_i = 0) &= 1 - \lambda_i \\
\end{align}
$$

$P(X_i | X_1, \cdots, X_{i-1})$ requires $1 \times 2^{i-1} = 2^{i-1}$ parameters, because there are $2^{i-1}$ combinations of the observations for the conditional variables.

So taken together, the number of parameters the joint distribution $P(X_1, X_2, \cdots, X_n)$ requires is

$$
\begin{align}
1 + \sum_{i=2}^{n} 2^{i-1} &= \sum_{i=1}^{n} 2^{i-1} \\
&= \frac{1 - 2^n}{1 - 2} \\
&= 2^n - 1
\end{align}
$$

There is also a much simpler way to compute the number of parameters the joint distribution $P(X_1, X_2, \cdots, X_n)$ requires. The combinations of the observations is $2^n$, because $P(X_1, X_2, \cdots, X_n)$ is a probability distribution. So the number of parameters is just the degree of freedom, which is $2^n - 1$. It is intractable to compute the joint distribution $P(X_1, X_2, \cdots, X_n)$, even if all the variables are binary.

Independence Assumptions

If we know some of the variables are independent from each other, the number of random variables could be reduced. Let’s take an extreme example. Suppose all the variables are independent from each other, the factorization of the joint distribution will be

$$
\begin{align}
P(X_1, X_2, \cdots, X_n) &= P(X_1) P(X_2) \cdots P(X_n) \\
\end{align}
$$

Obviously, the number of the parameters required for the joint distribution in this case will be $n$, which is much more smaller than the $2^n - 1$, and it is tractable.

However, having independence assumptions does not always reduce the number of parameters significantly. Suppose we have the following independence assumptions, as reflected in the following Bayesian network,

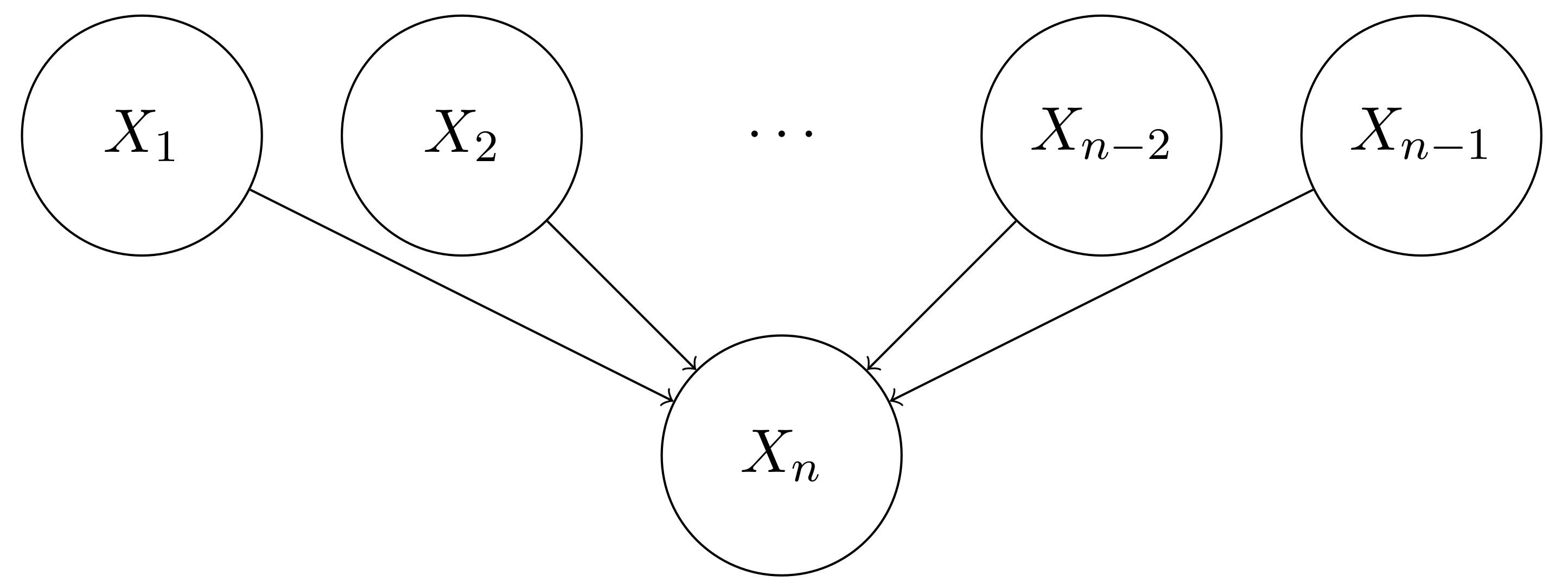
The factorization of the joint distribution $P(X_1, X_2, \cdots, X_n)$ could be simplified as

$$
\begin{align}
P(X_1, X_2, \cdots, X_n) &= P(X_1) P(X_2) \cdots P(X_{n-1}) P(X_n | X_1, \cdots, X_{n-1}) \\
\end{align}
$$

With our experience in computing the number of parameters for the chain rule case, it is not hard to find that the number of parameters required for the joint distribution in this case is $(n - 1) + 1 \times 2^{n-1} = 2^{n-1} + n - 1$. It is still intractable!

It should be noted that the above Bayesian network that has multiple independent causes is actually very common in practice. For example, $X_n$ could be the symptom of cough, and $X_1, X_2, \cdots, X_{n-1}$ could be the diseases that cause cough. We definitely want to use much fewer number of parameters to represent this joint distribution.

Additional Structured Assumptions

In order to further reduce the number of parameters for the model, the one that have multiple independent causes in particular, we have to pose more assumptions.

We introduce a series of additional random variables $Z_0, Z_1, Z_2, \cdots, Z_{n-1}, Z_{n}$, such that for $i \in [0, n-1]$,

$$
\begin{align}
P(Z_i = 0 | X_i = 0) &= 1 \\
P(Z_i = 1 | X_i = 0) &= 0 \\
P(Z_i = 0 | X_i = 1) &= 1 - \alpha_i \\
P(Z_i = 1 | X_i = 1) &= \alpha_i \\
\end{align}
$$

This will increase the number of parameters by $n - 1$.

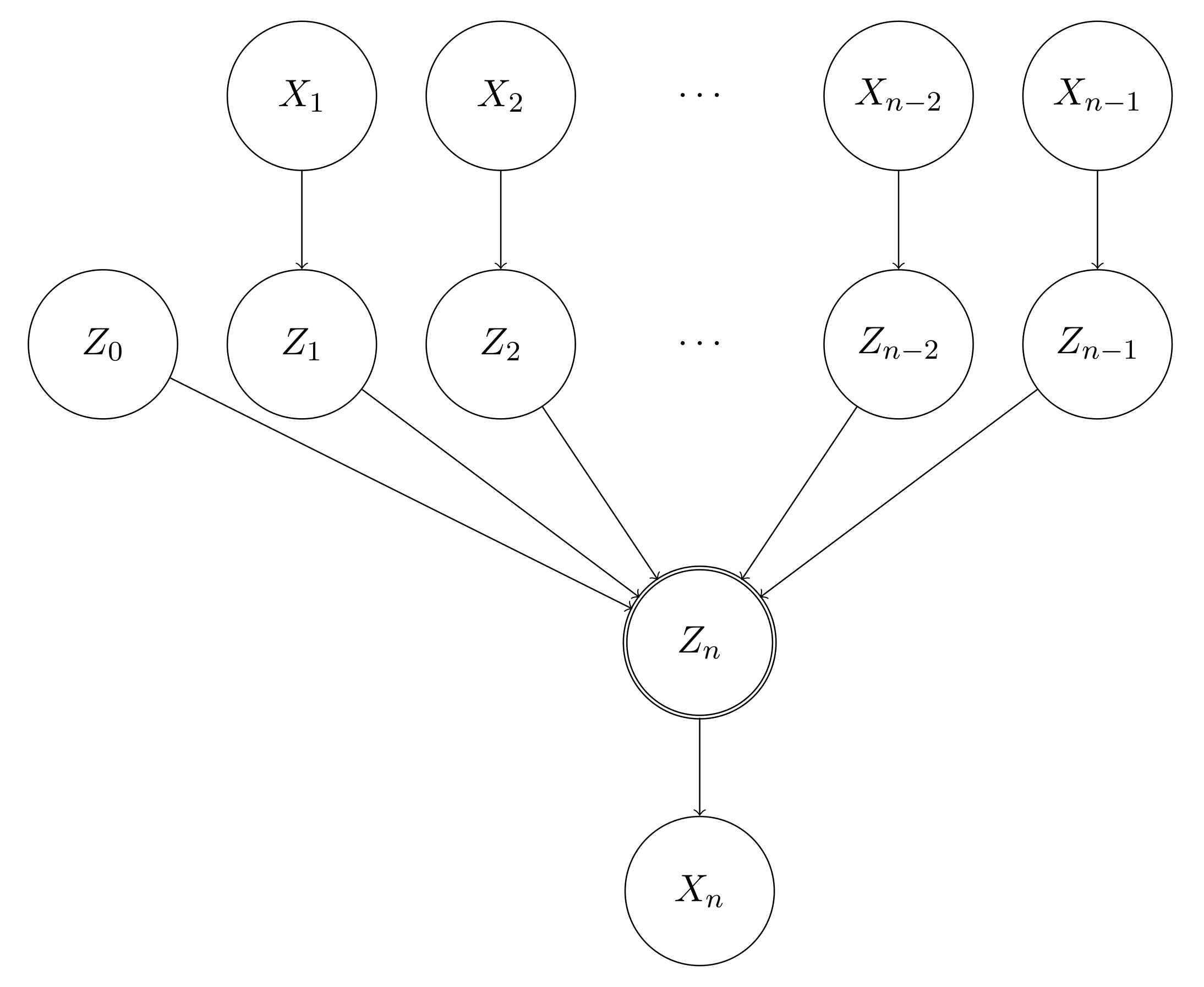
$$
Z_n = f(Z_0, Z_1, \cdots, Z_n)
$$

where $f$ is a deterministic function, such as $\text{OR}$, $\text{Max}$, $\text{Sum}$, etc.

Suppose $f$ is $\text{OR}$, and we have the following $P(X_n | Z_n)$,

$$
\begin{align}
P(X_n = 0 | Z_n = 0) &= 1 \\
P(X_n = 1 | Z_n = 0) &= 0 \\
P(X_n = 0 | Z_n = 1) &= 0 \\
P(X_n = 1 | Z_n = 1) &= 1 \\
\end{align}
$$

We will find that this is actually very good assumptions for the scenarios such as multiple independent diseases causing a symptom.

Let’s further count how many parameters are required for computing the joint distribution.

$$
\begin{align}
P(X_n = 0 | X_1, X_2, \cdots, X_{n-1}) &= (1 - \alpha_0) \prod_{i=1}^{n-1} (1 - \alpha_i) \\
&= \prod_{i=0}^{n-1} (1 - \alpha_i) \\
\end{align}
$$

$$
\begin{align}
P(X_n = 1 | X_1, X_2, \cdots, X_{n-1}) &= 1 - P(X_n = 0 | X_1, X_2, \cdots, X_{n-1}) \\
&= 1 - \prod_{i=0}^{n-1} (1 - \alpha_i) \\
\end{align}
$$

$$
\begin{align}
P(X_1, X_2, \cdots, X_{n-1}) &= P(X_1) P(X_2) \cdots P(X_{n-1}) \\
\end{align}
$$

$$
\begin{align}
P(X_1, X_2, \cdots, X_{n}) &= P(X_1, X_2, \cdots, X_{n-1}) P(X_n | X_1, X_2, \cdots, X_{n-1})\\
\end{align}
$$

Comparing with the case that only has independence assumptions, we now only need $n$ variables to represent the conditional distribution $P(X_n | X_1, X_2, \cdots, X_{n-1})$. The number of variables required for the joint distribution $P(X_1, X_2, \cdots, X_{n})$ is thus $(n - 1) + n = 2n - 1$. It becomes tractable now!

Actually, this probabilistic graph looks quite familiar to the people who studies machine learning. If we remove the probabilistic nature of the Bayesian network from the graph and add weights to the edge of the connections, we will immediately find that this is actually a neural network, such as a single-layer perceptron with a sigmoid activation layer.

Conclusion

We have shown how to reduce the number of parameters required to represent the probabilistic graphical model by posing assumptions.

References

• Knowledge Engineering for Large Belief Networks