Deformable Convolution
Introduction
Convolution is a fundamental operation in computer vision. However, it has some inherent limitations which prevented the neural network from learning a computer vision task even better. For example, the receptive field of an output pixel in convolution layer is always fixed and each output pixel in the convolution layer always have the same receptive field size and shape. Apparently, the pixel corresponds to the background, the pixel corresponds to a small object, and the pixel corresponds to a large object should have different receptive field size and shape. This means that the convolution receptive field cannot be changed and cannot be adapted to the input data.
Deformable convolution was proposed to address this limitation. It allows the receptive field to be changed and adapted to the input data. This is done by learning the spatial sampling locations of the convolution kernel.
In this blog post, we will quickly describe the deformable convolution and deformable convolution v2.
Deformable Convolution
Deformable convolution learns an offset for each spatial location of the vanilla convolution kernel. The offset is then added to the spatial location of the vanilla convolution kernel. The new spatial location is then used to sample the input feature map for convolution, usually via interpolations.
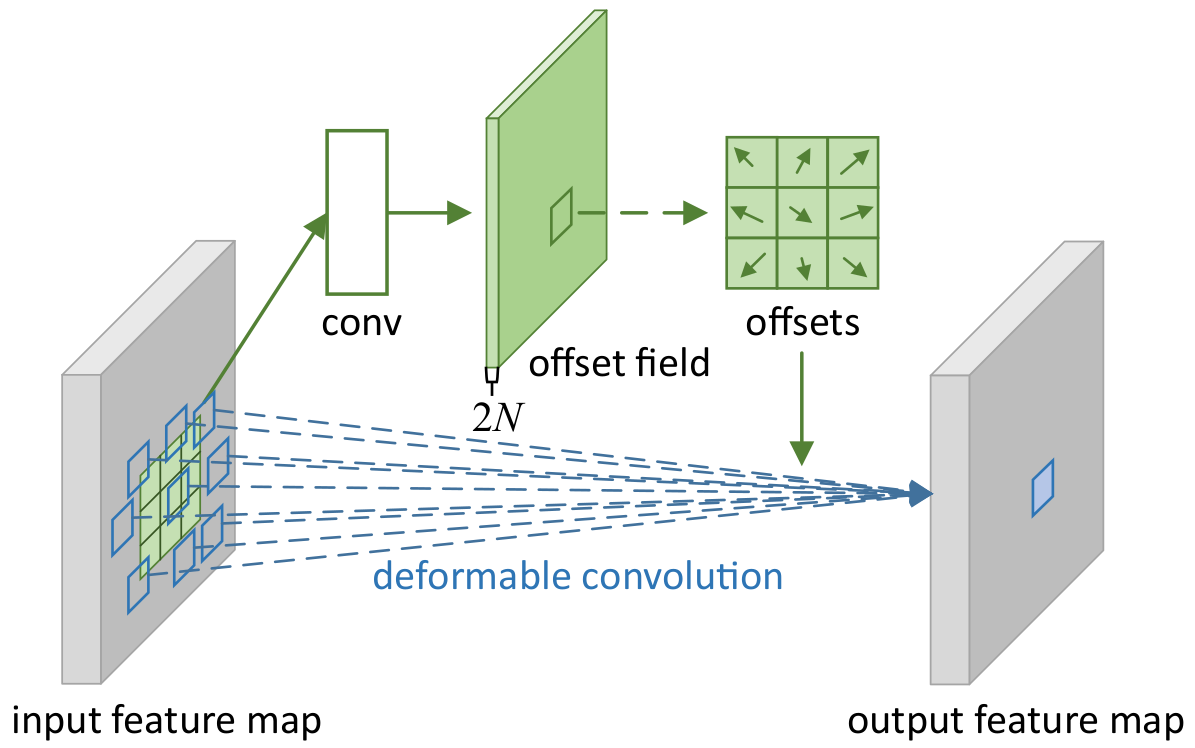
Given an input feature map $\mathbf{x}$, a convolution kernel $\mathbf{w}$, and a convolution receptive field $\mathcal{R}$ which defines the fixed spatial sampling location of the kernel, the value at the location $\mathbf{p}$ of the output feature map $\mathbf{y}$ is computed as follows:
$$
\begin{aligned}
\mathbf{y}(\mathbf{p}) &= \sum_{\mathbf{p}_{k} \in \mathcal{R}}^{} \mathbf{w}(\mathbf{p}_{k}) \mathbf{x}(\mathbf{p} + \mathbf{p}_{k}) \\
\end{aligned}
$$
where $\mathbf{p}_{k}$ is the fixed spatial sampling location of the kernel.
Deformable convolution learns an offset $\Delta\mathbf{p}$ for each spatial location of the kernel. The offset is then added to the spatial location of the kernel. The new spatial location is then used to sample the input feature map for convolution, usually via interpolations. The value at the location $\mathbf{p}$ of the output feature map $\mathbf{y}$ is computed as follows:
$$
\begin{aligned}
\mathbf{y}(\mathbf{p}) &= \sum_{\mathbf{p}_{k} \in \mathcal{R}}^{} \mathbf{w}(\mathbf{p}_{k}) \mathbf{x}(\mathbf{p} + \mathbf{p}_{k} + \Delta\mathbf{p}_{k}) \\
\end{aligned}
$$
where $\Delta\mathbf{p}_{k}$ is the offset for the fixed spatial location $\mathbf{p}_{k}$ of the kernel and is usually learned by a convolution layer of the same receptive field size and shape,
$$
\begin{aligned}
\Delta\mathbf{p}_{k} &= \sum_{\mathbf{p}_{i} \in \mathcal{R}}^{} \mathbf{w}_{k}^{\prime}(\mathbf{p}_{i}) \mathbf{x}(\mathbf{p} + \mathbf{p}_{i}) \\
\end{aligned}
$$
and $\mathbf{x}(\mathbf{p} + \mathbf{p}_{k} + \Delta\mathbf{p}_{k})$ can be interpolated from the neighboring pixels.
Because deformable convolution and vanilla convolution have exactly the same input tensor shape and output tensor shape, they can be used interchangeably.
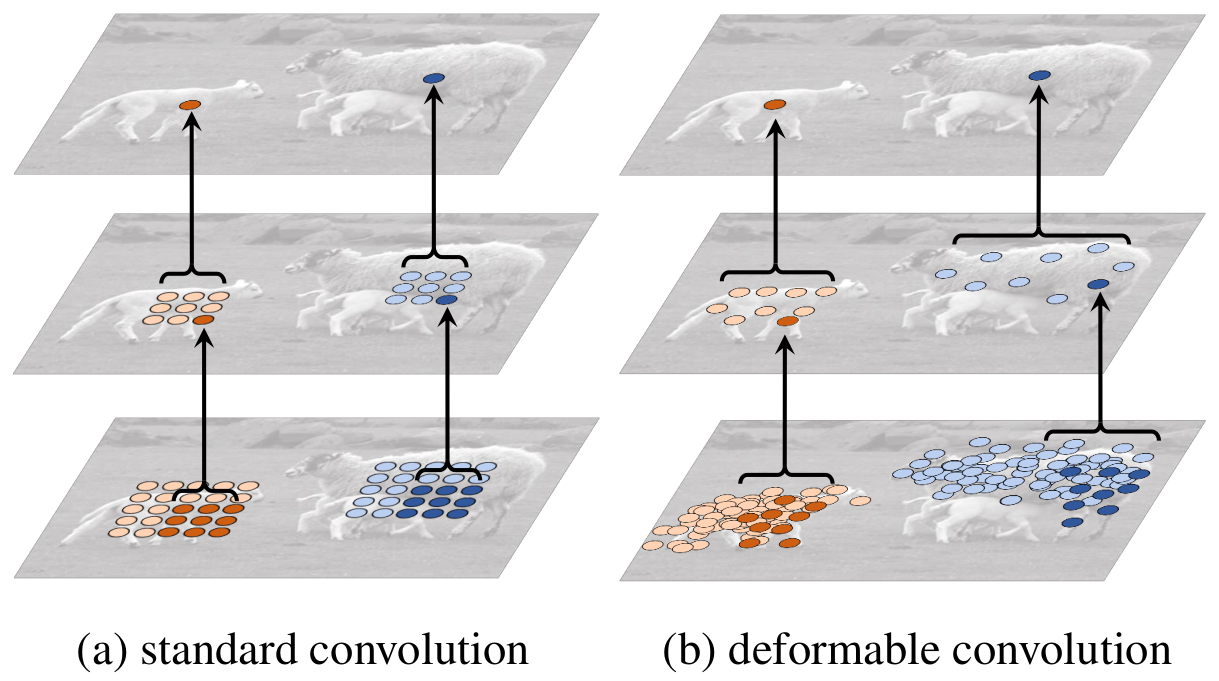
Here is an illustration of the receptive field of a vanilla convolution and a deformable convolution for the same pixel on the same image.
Deformable Convolution V2
Even though deformable convolution allows the receptive field to be changed and adapted to the input data, the receptive field sometimes goes out of the object boundary. Because the weights of the convolution kernel are fixed after learning, the pixels outside the object boundary will make unnecessary contributions to the output feature map. To address this issue, deformable convolution v2 was proposed and it introduced a learned scalar that depends on the input data to modulate the amplitude of each pixel contributions.
Similar to how the offset was learned in deformable convolution, deformable convolution v2 learns a scalar between 0 and 1 for each spatial location of the kernel. The scalar is then multiplied to the value of the input feature map at the spatial location of the kernel, and this scalar is used for modulating the amplitude of each pixel contributions. The value at the location $\mathbf{p}$ of the output feature map $\mathbf{y}$ is computed as follows:
$$
\begin{aligned}
\mathbf{y}(\mathbf{p}) &= \sum_{\mathbf{p}_{k} \in \mathcal{R}}^{} \mathbf{w}(\mathbf{p}_{k}) \mathbf{x}(\mathbf{p} + \mathbf{p}_{k} + \Delta\mathbf{p}_{k}) \Delta\mathbf{m}(\mathbf{p}_{k}) \\
\end{aligned}
$$
where $\Delta\mathbf{m}(\mathbf{p}_{k}) \in [0, 1]$ is the scalar modulation factor for the fixed spatial location $\mathbf{p}_{k}$ of the kernel and is usually learned by a convolution layer of the same receptive field size and shape.
$$
\begin{aligned}
\Delta\mathbf{m}(\mathbf{p}_{k}) &= \sum_{\mathbf{p}_{i} \in \mathcal{R}}^{} \mathbf{w}_{k}^{\prime\prime}(\mathbf{p}_{i}) \mathbf{x}(\mathbf{p} + \mathbf{p}_{i}) \\
\end{aligned}
$$
Because deformable convolution v2, deformable convolution, and vanilla convolution have exactly the same input tensor shape and output tensor shape, they can also be used interchangeably.
References
Deformable Convolution