Evolved Transformer Explained
Introduction
In the paper “The Evolved Transformer”, Evolution algorithm has been applied for finding better neural network architecture for Transformer derivatives. The Transformer architecture was represented using a vector of discrete values, the fitness was represented using the perplexity of the language translation, and the evolution algorithm was used for finding offsprings that have better fitness.
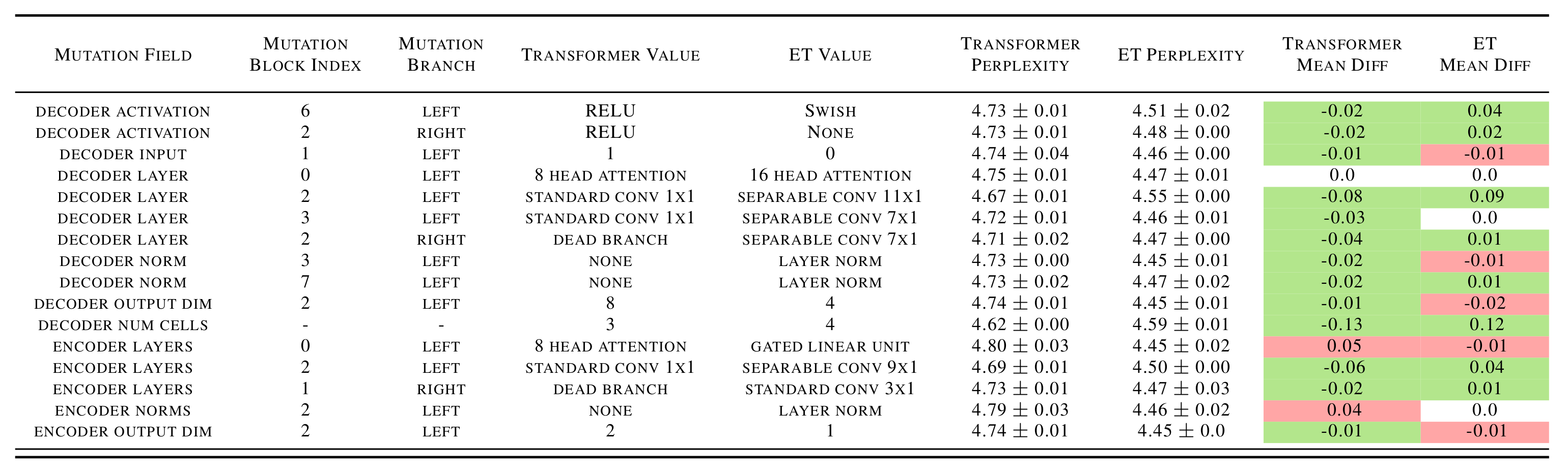
The entire research was rather conventional. However, there are a couple of places that are confusing to the readers, especially those who have read the original Transformer paper “Attention Is All You Need”, because some of the notations are not consistent. In this blog post, I would like to explain some of the key parts in the paper that have not been well explained.
Evolved Transformer
Block and Cell
In the original Transformer paper, the authors described the repetitive components in the encoder or decoder as layers. The particular model described in the paper has 6 layers of encoder and 6 layers of decoders. However, in the Evolved Transformer paper, they used “block” and “cell” to describe the architecture of Transformer. For the exact same Transformer model used in the original Transformer paper, they said the encoder has 6 blocks, the decoder has 8 blocks, and the number of cells, which is the number of repetitions of the cells, is 3. This actually caused a lot of confusion.
In fact, the 6 blocks of one cell for the original Transformer encoder represents 2 repetitive layers of the original Transformer encoder, and the 8 blocks of one cell for the original Transformer decoder represents 2 repetitive layers of the original Transformer decoder. It is also equivalent to say one layer of the original Transformer encoder represents 3 blocks, and one layer of the original Transformer decoder represents 4 blocks.
So if the cell was repeated 3 times, there are $6 \times 3 = 18$ and $8 \times 3 = 24$ blocks for the original Transformer encoder and decoder, respectively. Calculating based on the number of layers also give the same number of blocks for both the encoder and the decoder.
Let’s see how the model was divided into blocks and cells.
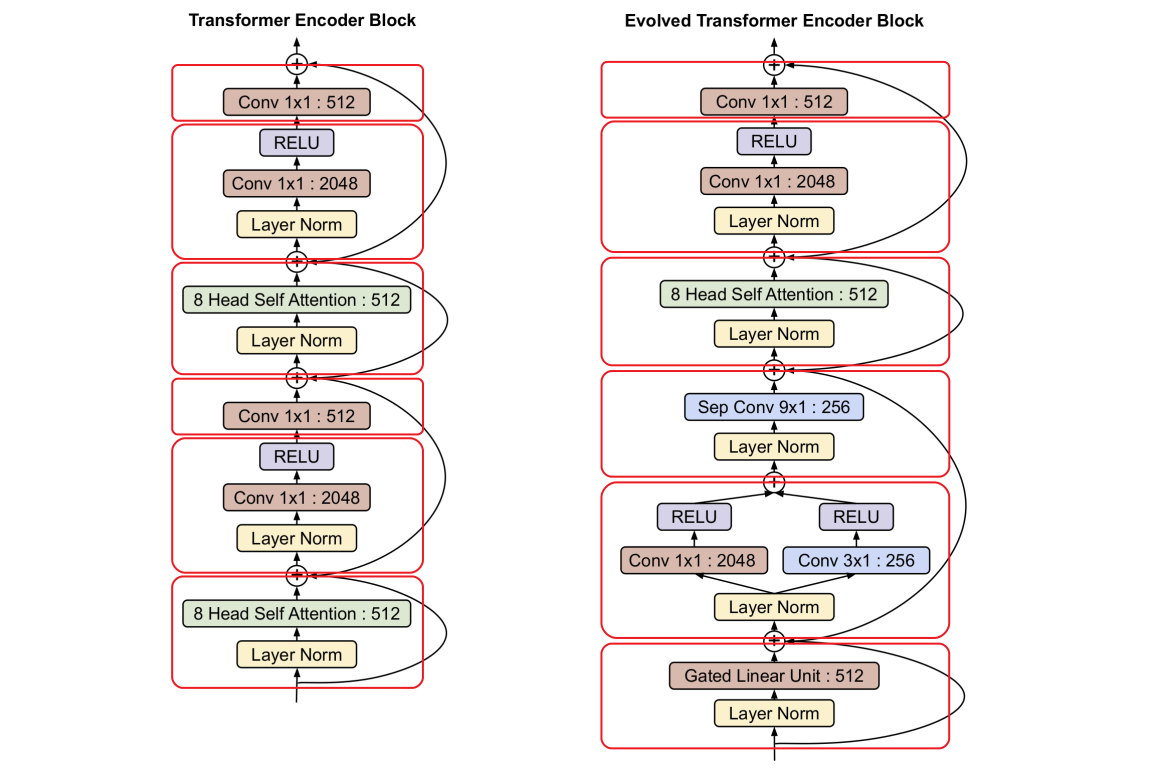
This figure is modified from the original figure from the paper. The notations in the figure from the original paper are confusing because instead of being a block, it is a cell. The blocks in the cell are highlighted using red rectangles.
We could unambiguously see that the original Transformer encoder cell consists of two repetitive components totally 6 blocks, and the first 3 blocks in the cell are equivalent to the one layer in the original Transformer encoder. After evolution, the Evolved Transformer encoder cell still has 6 blocks of components.
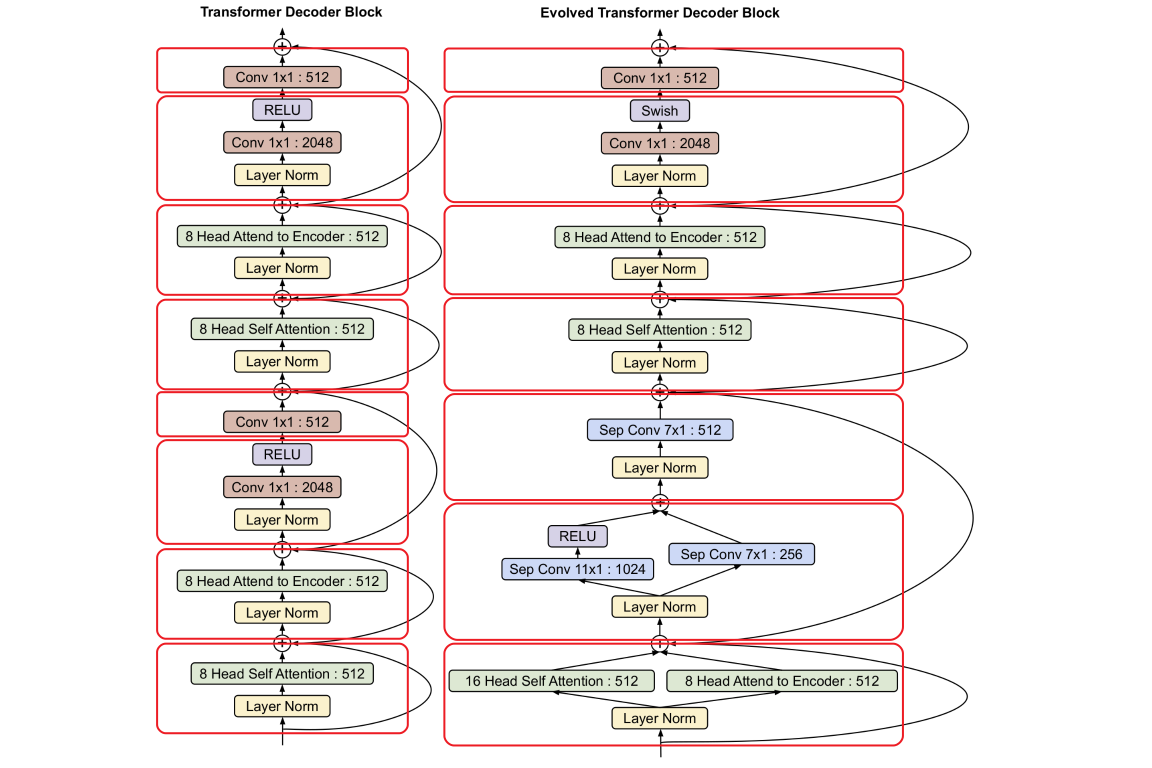
Similarly, we could unambiguously see that the original Transformer decoder cell consists of two repetitive components totally 8 blocks, and the first 4 blocks in the cell are equivalent to the one layer in the original Transformer decoder.
Sounds good. Wait, after evolution, the Evolved Transformer decoder cell only has 7 blocks of components! This is because after evolution, the first two blocks in the original Transformer decoder “merged to” one block. To be exact, in the neural network architecture, the Evolved Transformer decoder does still have 8 blocks, however, the author plot the figure in a way that it looks like there are only 7 blocks left.
Note that the “Decoder Input” has been evolved from 1 in the original Transformer to 0 in the Evolved Transformer. That is why the first two blocks were “merged” to one block in the figure.
Two Branches
In the original Transformer, the skip connections could be represented using a branch natively where the branch contains an identity node and the input to the right branch could be different from the input to the left branch. If there is no skip connection or a second branch in the block, the branch is represented using “Death Branch”. The “Death Branch” could evolve to something that has actual nodes.
Other FAQs
There is a YouTube video covering some of the basics of the paper, such as the vector representation for the blocks. However, it does not cover any of the things I described above, which I think is extremely necessary for understanding the algorithm.
References
Evolved Transformer Explained