Focus Breathing and Compensation
Introduction
Focus breathing, also known as lens breathing, is the phenomenon where the field of view (FOV) of a camera lens changes when the focus distance changes. This effect is particularly noticeable in videography when the focus is pulled from one subject to another at different distances, causing a change in composition that can be distracting to viewers.
Even though focus breathing is a common phenomenon, I hardly found any detailed explanation of the underlying physics and mathematics, not to mention how focus breathing compensation is implemented. In this blog post, I will explain the physics and mathematics behind focus breathing and focus breathing compensation.
Thin Lens Equation
The thin lens equation is the fundamental equation that is used for deriving the FOV equation.
Assuming the thickness of the lens is infinitely small, the thin lens equation
$$
\frac{1}{f} = \frac{1}{u} + \frac{1}{v}
$$
where $f$ is the focal length, $u$ is the object distance to the lens, $v$ is the image distance to lens.
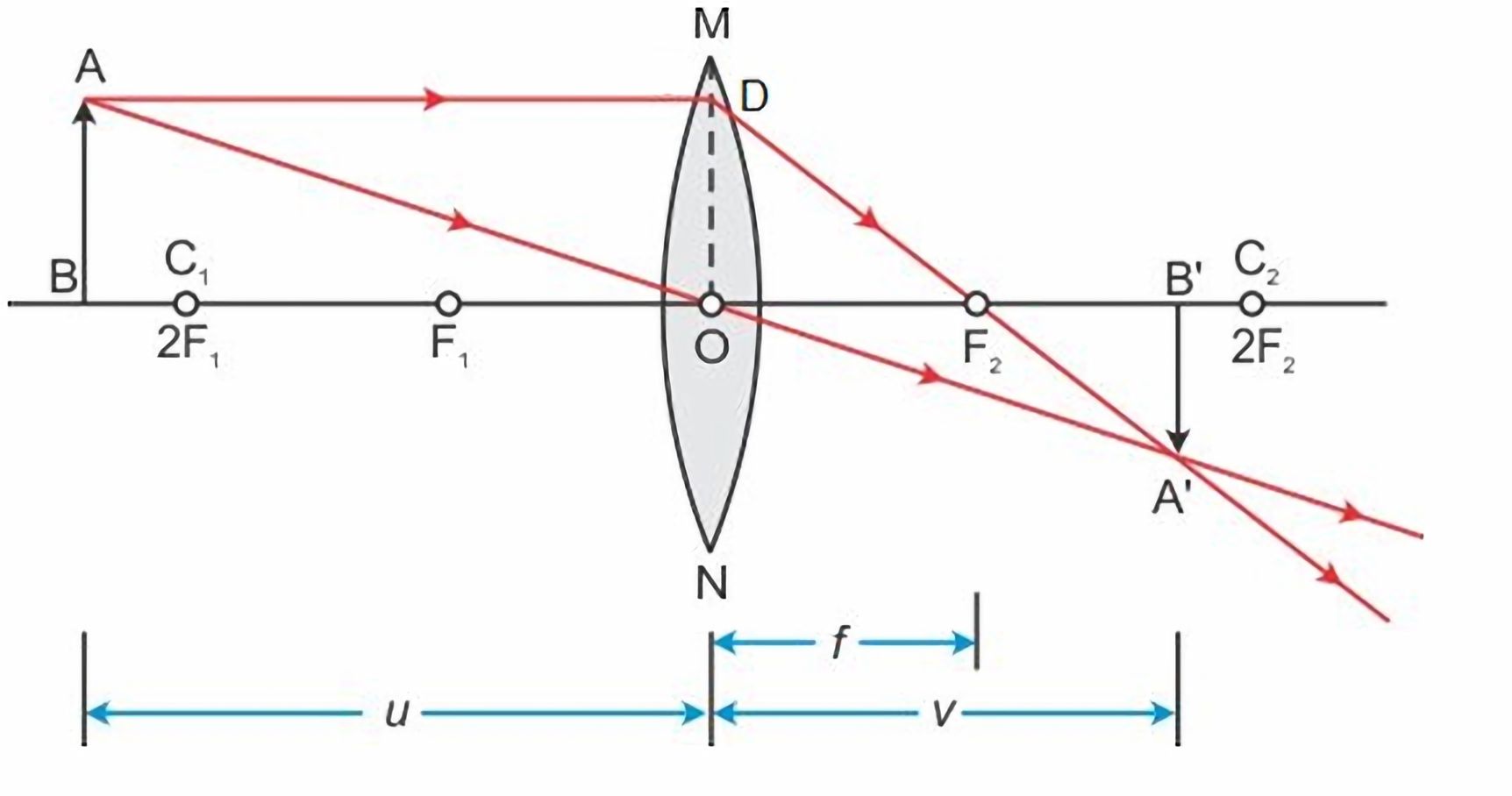
The proof of the thin lens equation can be found in my previous blog post “How Camera Lens Works”.
Field of View
Suppose the focus plane is at the object $AB$. The object distance to the lens is $u$, the image distance to the lens is $v$, the focal length of the lens is $f$, and the sensor size is $d$. Based on the simple geometry, we have
$$
\tan \left( \frac{\theta}{2} \right) = \frac{\frac{d}{2}}{v} = \frac{d}{2v}
$$
where $\theta$ is the field of view angle.
Solving this equation, we have
$$
\theta = 2 \arctan \left( \frac{d}{2v} \right)
$$
With the thin lens equation, we have
$$
v = \frac{uf}{u - f}
$$
Therefore, the field of view angle $\theta$ can be expressed as
$$
\theta = 2 \arctan \left( \frac{d (u - f)}{2uf} \right)
$$
When $u = \infty$ or $u \gg f$, we have $v \approx f$, and the field of view angle $\theta$ can be approximated as
$$
\theta \approx 2 \arctan \left( \frac{d}{2f} \right)
$$
Focus Breathing and Compensation In Videography
Focus breathing is the change of the field of view when the focus distance changes. From the above field of view equation, we can see that when the object distance $u$ changes, especially when $u$ is not very large compared to the focal length $f$, the field of view angle $\theta$ also changes.
In videography, focus breathing is usually undesirable. When the close object in focus is moving, the field of view also changes, which could be distracting to viewers. Therefore, some high-end camera systems are designed to minimize focus breathing, which is sometimes referred to as focus breathing compensation.
Based on the field of view angle equation,
$$
\theta = 2 \arctan \left( \frac{d (u - f)}{2uf} \right)
$$
we know that to maintain a constant field of view angle $\theta$, when the object distance $u$ changes, we could adjust the focal length $f$ or the sensor size $d$ accordingly.
It is impossible to adjust the focal length $f$ for prime lenses. So it is more common to adjust the sensor size $d$, equivalently cropping the images, usually in real time during video recording, so that the field of view angle $\theta$ remains constant when the focus distance $u$ changes. This is how focus breathing compensation is usually implemented in high-end camera systems.
Suppose at time step $t_{0}$, the object distance is $u_{0}$, the focal length is $f$, the sensor size is $d_{0}$, and the field of view angle is $\theta_{0}$.
$$
\theta_{0} = 2 \arctan \left( \frac{d_{0} (u_{0} - f)}{2u_{0}f} \right)
$$
At time step $t_{1}$, the object distance changes to $u_{1}$, the focal length remains the same $f$, the sensor size is adjusted to $d_{1}$, and the field of view angle is $\theta_{1}$.
$$
\theta_{1} = 2 \arctan \left( \frac{d_{1} (u_{1} - f)}{2u_{1}f} \right)
$$
To maintain the same field of view angle, we have $\theta_{1} = \theta_{0}$, which gives us
$$
d_{1} = d_{0} \cdot \frac{u_{1} (u_{0} - f)}{u_{0} (u_{1} - f)}
$$
Focus Breathing and Compensation In Photography
In photography, focus breathing is usually less of a concern. But there are some use cases, such as focus stacking where multiple images with different focus distances are taken and combined to produce an image with a larger depth of field. In these use cases, focus breathing could cause misalignment between images, making it difficult to combine them properly.
Focus Breathing Compensation Implemented In Sony Camera Systems
References
Focus Breathing and Compensation