How Camera Lens Works
Introduction
Camera lens is one of the key components for the camera systems. Nowadays, cameras are used everywhere, smart phones, surveillance systems, military weapons, etc. The camera lens descriptions can sometimes be confusing to the beginner users.
In this blog post, I will discuss how camera lens works using simple physics theories and delve into the camera lens used in smart phones which most of the users care about.
Thin Lens Equation
Assuming the thickness of the lens is infinitely small, the thin lens equation
$$
\frac{1}{f} = \frac{1}{u} + \frac{1}{v}
$$
where $f$ is the focal length, $u$ is the object distance to the lens, $v$ is the image distance to lens.
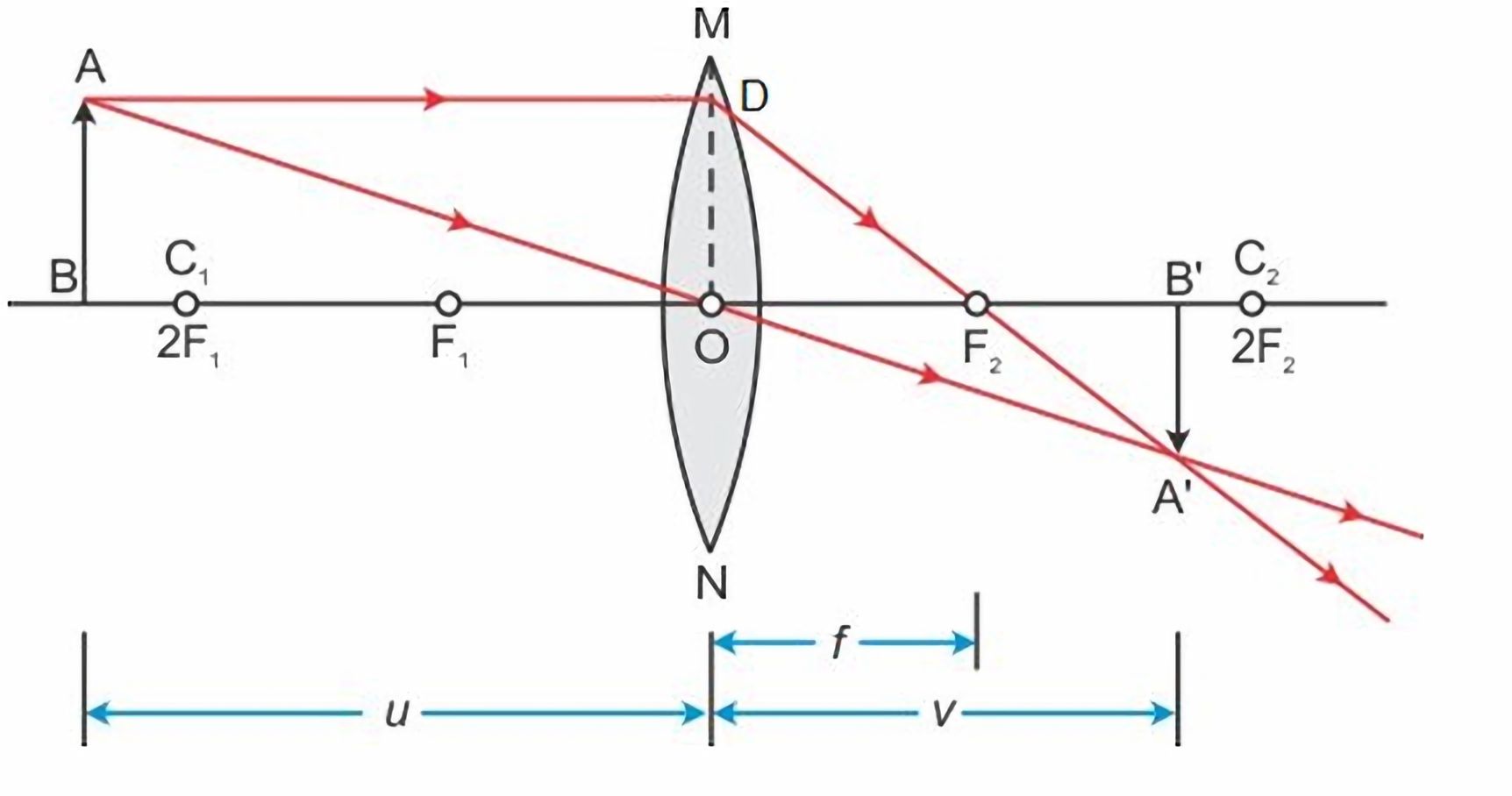
Proof
Using the properties of similar triangles, we have
$$
\begin{align}
u &= \left\vert \text{AD} \right\vert = \left\vert \text{OB} \right\vert \\
v &= \left\vert \text{OB}^{\prime} \right\vert \\
f &= \left\vert \text{OF}_{1} \right\vert = \left\vert \text{OF}_{2} \right\vert \\
\end{align}
$$
$$
\begin{align}
\frac{f}{u} &= \frac{\left\vert \text{OF}_{2} \right\vert}{\left\vert \text{AD} \right\vert} = \frac{\left\vert \text{A}^{\prime}\text{F}_{2} \right\vert}{\left\vert \text{A}^{\prime}\text{D} \right\vert}
\end{align}
$$
$$
\begin{align}
\frac{f}{v} &= \frac{\left\vert \text{OF}_{2} \right\vert}{\left\vert \text{OB}^{\prime} \right\vert} = \frac{\left\vert \text{DF}_{2} \right\vert}{\left\vert \text{A}^{\prime}\text{D} \right\vert}
\end{align}
$$
$$
\begin{align}
\frac{f}{u} + \frac{f}{v} &= \frac{\left\vert \text{A}^{\prime}\text{F}_{2} \right\vert}{\left\vert \text{A}^{\prime}\text{D} \right\vert} + \frac{\left\vert \text{DF}_{2} \right\vert}{\left\vert \text{A}^{\prime}\text{D} \right\vert} \\
&= \frac{\left\vert \text{A}^{\prime}\text{D} \right\vert}{\left\vert \text{A}^{\prime}\text{D} \right\vert} \\
&= 1 \\
\end{align}
$$
Therefore,
$$
\frac{1}{f} = \frac{1}{u} + \frac{1}{v}
$$
This concludes the proof. $\square$
Thin Lens Consequences
From the thin lens diagram, we could see that the larger $u$ is, the smaller $v$ is. Therefore, $\frac{v}{u}$ will be small for objects that are very far.
Because
$$
\begin{align}
\frac{v}{u} &= \frac{\left\vert \text{A}^{\prime}\text{B}^{\prime} \right\vert}{\left\vert \text{AB} \right\vert}
\end{align}
$$
Given a fixed size sensor, assuming the sensor is allowed to move, the farther the object is, the smaller the object is captured on the sensor. This is why we found things look small when they are far away from us but large when they are close to us.
To see a larger far-distance object on the sensor, we can increase the focal length $f$, usually by adjusting the lens property or using a different lens.
Large sensor size is always better, because we can always capture more information. The image captured using a smaller sensor at the same image distance $v$ can always be cropped from the image captured in a larger sensor.
If $u \gg f$, which is usually the case for most of the ordinary camera applications, $f \approx v$. This means for those cameras, the sensor is almost located at the focal point.
Equivalent Focal Length
Nowadays, smart phones have equipped very good cameras. However, the phone camera descriptions are usually very confusing.
For example, iPhone 15 Pro Max 48MP Main camera is described “48MP Main: 24 mm, ƒ/1.78 aperture, second‑generation sensor‑shift optical image stabilization, 100% Focus Pixels, support for super‑high‑resolution photos (24MP and 48MP)”.
We know that the sensor has to be placed behind the focal point to capture a sharp image. But today’s smart phone are usually very thin, sometimes even thinner than 10 mm. How does a lens of 24 mm focal length work in a smart phone which has a thickness of 10 mm?
It turns out that the focal length that smart phones refer to are not the focal length we described in the thin lens diagram. The focal length numbers stated in the specs of smart phone cameras are stated as equivalent to those of a 35 mm full-frame sensor camera. The actual focal length of smartphone camera lenses is much, much shorter than what’s stated.
Concretely, a 35 mm full-frame camera sensor has a diagonal length of 35 mm. Suppose the smart phone camera sensor has a diagonal length of $d$ mm, it has a crop factor of $\frac{35}{d}$. Let’s then derive how the equivalent focal length is calculated for the smart phone camera lens.
Suppose a distant object captured on the image has a length of $h$ on the $d$ mm camera sensor and a length of $h^{\prime}$ on the 35 mm camera sensor. To make the two images captured from the two camera systems look the “same”, i.e., the same after rescaling one of them, we must have $\frac{h}{d} = \frac{h^{\prime}}{35}$, i.e., $\frac{h}{h^{\prime}} = \frac{d}{35}$. This means $\frac{h}{h^{\prime}}$ just happens to be the inverse of crop factor.
From the thin lens diagram, we know that the image distances from the two camera systems, $v$ and $v^{\prime}$ for the $d$ mm camera sensor and 35 mm camera sensor respectively, have the relationship $\frac{v}{v^{\prime}} = \frac{h}{h^{\prime}}$ because of similar triangles. Remember, we have derived previously that $f \approx v$. So the focal length for the for the $d$ mm camera sensor and 35 mm camera sensor respectively, $f$ and $f^{\prime}$, must have $\frac{f}{f^{\prime}} = \frac{h}{h^{\prime}} = \frac{d}{35}$. This means $\frac{f}{f^{\prime}}$ is also just the inverse of crop factor.
Typically, the smart phone camera sensor is very small comparing to a full-frame camera sensor. For example, iPhone 15 Pro Max might have a camera sensor of diagonal length of 5.6 mm, a crop factor of $\frac{35}{d} = \frac{35}{5.6} = 6.25$. The equivalent focal length of the 48MP Main camera corresponding to a 35 mm full-frame camera sensor is $f = 24$ mm. So we must have $\frac{f}{f^{\prime}} = \frac{d}{35} = \frac{5.6}{35}$. The actual focal length of the lens in the smart camera is just $f^{\prime} = \frac{5.6}{35} f = \frac{5.6}{35} \times 24 = 3.84$ mm. This can be fit into a modern thin smart phone perfectly.
Someone might also ask, what if the smart phone manufacturers use even smaller sized sensor? Well, the consequence is, without changing the camera lens, the smart phone camera lens equivalent focal length becomes larger, and the smart phone manufacturers can fool the customers as if the smart phone camera can capture even farther objects sharply if they want. But as I mentioned previously, using smaller camera sensor makes it a even smaller crop equivalent from the 35 mm camera sensor, the image quality from a smaller camera sensor will be much worse after rescaling. If one smart phone manufacturer is playing this trick to fool the customers, it can be immediately identified by comparing quality of its image against the images from other smart phone cameras. Without using advanced interpolation or artificial intelligence algorithms, assuming all the other factors in the two smart phone camera systems are comparable, the image qualities from the smaller camera sensor can hardly beat the ones from the larger camera sensor.
Telephoto Lens
A telephoto lens, in photography and cinematography, is a specific type of a long-focus lens in which the physical length of the lens is shorter than the focal length. Even if smart phone cameras use equivalent focal length to describe their lenses, they might not use telephoto lens if there is no need to use lenses with even larger focal length to capture even farther objects.
In recent years, more and more smart phone manufacturers, including Apple, start to produce smart phone cameras that has very long focal lengths to capture telephotos. Taking iPhone 15 Pro Max 12MP 5x Telephoto camera as an example, “12MP 5x Telephoto: 120 mm, ƒ/2.8 aperture, 3D sensor‑shift optical image stabilization and autofocus, tetraprism design. 5x optical zoom in, 2x optical zoom out; 10x optical zoom range. Digital zoom up to 25x”. The 12MP 5x Telephoto camera has a equivalent focal length of 120 mm. After translating it to the actual focal length, it is $f^{\prime} = \frac{5.6}{35} f = \frac{5.6}{35} \times 120 = 19.2$ mm, which is much larger than the thickness of the smart phone. Now the telephoto lens can come into play because it can make the physical length shorter than the actual focal length. It’s not some new technique and it’s original form has been used in applications such as submarine periscopes. Many smart phone manufacturers use periscope designs for their telephoto cameras whereas Apple uses tetraprism design. We will not go into the details of different telephoto lens designs in this article.

Telephoto lens is not perfect and everything comes with a cost. Using telephoto lens will lose more photons comparing to using ordinary lens with the equivalent focal length.
Conclusions
Using the thin lens assumption and thin lens equation, we could understand how camera lens works in different applications at a high level.
References
How Camera Lens Works