Gated Linear Units (GLU) and Gated CNN

Introduction

I created an implementation for CycleGAN based voice conversion a few years ago. In the neural network, the original authors used a new gating mechanism to control the information flow, which is somewhat similar to the self-attention mechanism we are using today. The gating mechanism is called Gated Linear Units (GLU), which was first introduced for natural language processing in the paper “Language Modeling with Gated Convolutional Networks”. The major difference between gating and self-attention is that gating only controls the bandwidth of information flow of a single neuron, while self-attention gathers information from a couple of different neurons.

Although GLU turns out to be intrinsically simple, the description of GLU from the original paper has been confusing to some of the readers. When I worked on the CycleGAN based voice conversion, I did not implement correctly for the first time. After a few years when I looked back at the paper, I almost misunderstood it again. The official PyTorch GLU function was also very confusing to the users.

In this blog post, I would like to walk through the GLU mechanism and elucidate some of the confusing parts in the original paper.

Gated Linear Units (GLU)

Mathematical Definition

In the original paper, given an input tensor, the hidden layer after the Gated CNN is as follows.

$$
\begin{align}
h(\mathbf{X}) = (\mathbf{X} \ast \mathbf{W} + \mathbf{b}) \otimes \sigma(\mathbf{X} \ast \mathbf{V} + \mathbf{c})
\end{align}
$$

where $m$, $n$ are respectively the number of input and output feature maps and $k$ is the patch size. Here, the number of input and output feature maps is just the number of channels, $k$ is just the kernel size, $\sigma$ is the sigmoid function, and $\otimes$ is the Hadamard product operator. $\mathbf{X} \in \mathbb{R}^{N \times m}$, $\mathbf{W} \in \mathbb{R}^{k \times m \times n}$, $\mathbf{b} \in \mathbb{R}^{n}$, $\mathbf{V} \in \mathbb{R}^{k \times m \times n}$, $\mathbf{c} \in \mathbb{R}^{n}$. Note that in this notation, the batch size is omitted.

Note that $\ast$ is not the symbol for tensor multiplication, it just denotes an operator between the two tensors on its two sides. (I know this is confusing!) In our context, $\ast$ is just a convolution operator. For 1D convolutions, the filter $\mathbf{W}$ has $k \times m \times n$ parameters, and the filter $\mathbf{V}$ also has $k \times m \times n$ parameters.

Usually, Gated CNN is conducted using 1D convolutions, where the input tensor $\mathbf{X}$ has dimensions of $[B,m,N]$, where $B$ is the batch size, $m$ is the number of channels, most likely the size of an embedding vector, and $N$ is the length of the token sequence.

OK, then the GLU mechanism should be simple and clear. Given a tensor, we do two independent convolutions and get two outputs. We further do an additional sigmoid activation for one of the outputs, and element-wise multiply the two outputs together.

Misleading Figure

The following figure illustrating Gated CNN and GLU, which I think is confusing, was copied from the original paper.

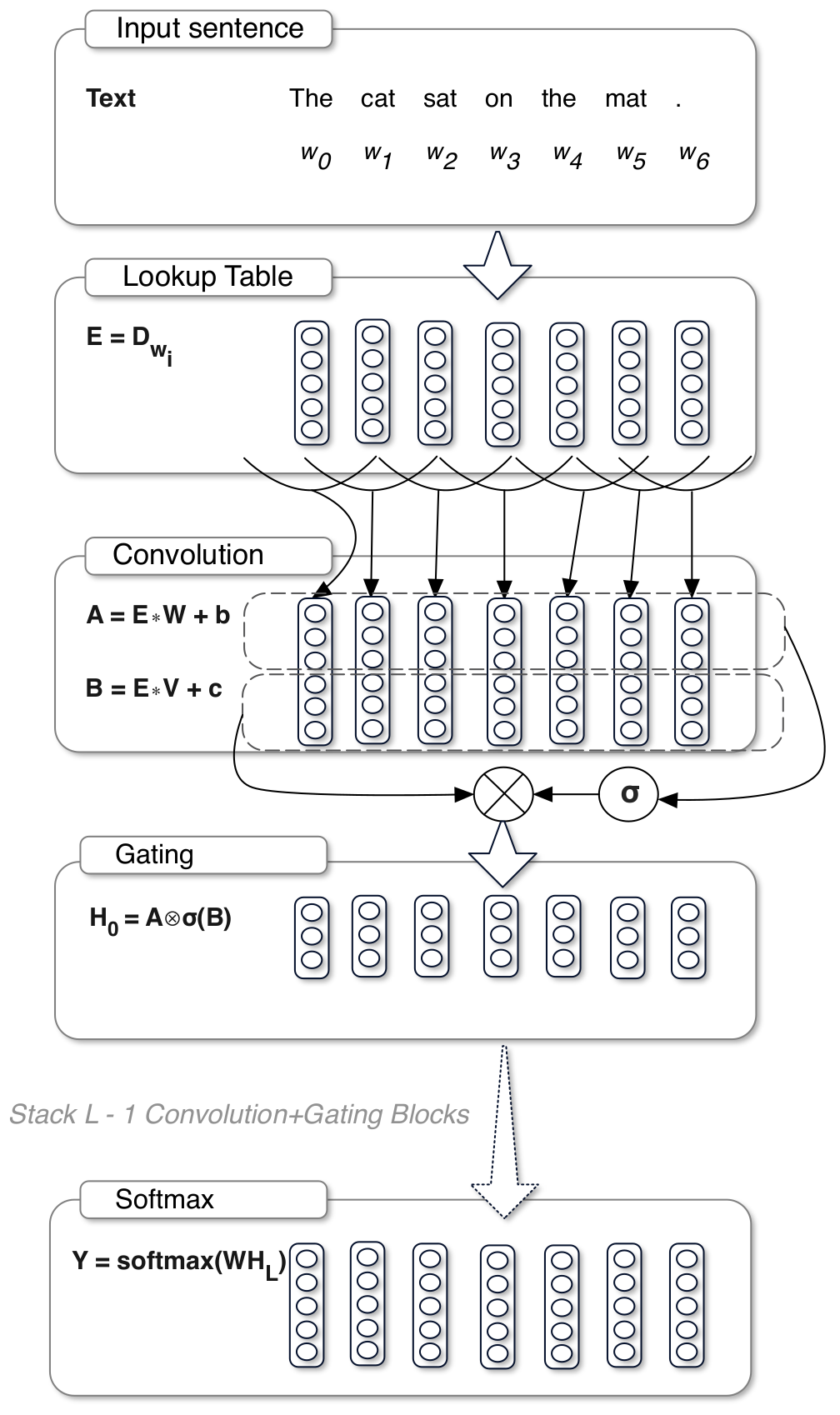
It looks as if the input tensor was split into two fractions, followed by convolutions and gating. However, this is wrong. If you look closer, you would find that the embedding vector size in the “Lookup Table” is 5, which could not be evenly split into two fractions for gating.

If I understand the figure correctly, the number of input channels from the input $\mathbf{E}$ is 5, and the number of output channels is 3. The author did not spend time to just separate the two outputs in the “Convolution” block and that is why the reader find it confusing. The last “Softmax” block is also confusing, since it reuses the symbol $\mathbf{W}$. However, this $\mathbf{W}$ has nothing to do with the previous $\mathbf{W}$ in the figure.

FAQs

PyTorch GLU Function

The official PyTorch GLU function split a given tensor evenly into two tensors along the specified dimension, does sigmoid for the second tensor and multiplied by the first tensor. If the user concatenates the two outputs from the two independent CNNs, and feed the concatenated tensor to the PyTorch GLU function, there would be nothing wrong. However, it is extremely confusing to readers because this concatenation step is actually not required to perform a correct GLU.

Conclusions

GLU simply refers to the step of computing $h(\mathbf{X})$. Gated CNN wraps the two independent CNNs and the GLU.

Gated CNN and GLU is simple and we should not be confused about them.