Group Lasso
Introduction
L1 (Lasso) and L2 (Ridge) regularization have been widely used for machine learning to overcome overfitting. Lasso, in particular, causes sparsity for weights. There is another regularization, which is something between Lasso and Ridge regularization, called “Group Lasso”, which also causes sparsity for weights.
In this blog post, we will first review Lasso and Ridge regularization, then take a look at what Group Lasso is, and understand why Group Lasso will cause sparsity for weights.
Notations
Suppose $\beta$ is a collection of parameters. $\beta = \{ \beta_1, \beta_2, \cdots, \beta_n \}$, The L0, L1, and L2 norms are denoted as $||\beta||_0$, $||\beta||_1$, $||\beta||_2$. They are defined as
$$
\begin{align}
||\beta||_0 &= \sum_{i=1}^{n} 1 \{\beta_i \neq 0\} \\
||\beta||_1 &= \sum_{i=1}^{n} |\beta_i| \\
||\beta||_2 &= \bigg(\sum_{i=1}^{n} \beta_i^2\bigg)^{\frac{1}{2}} \\
\end{align}
$$
Lasso and Ridge Regressions
Given a dataset $\{X, y\}$ where $X$ is the feature and $y$ is the label for regression, we simply model it as has a linear relationship $y = X\beta$. With regularization, the optimization problem of L0, Lasso and Ridge regressions are
$$
\begin{align}
\beta^{\ast} &= \operatorname*{argmin}_{\beta} ||y - X\beta||_2^{2} + \lambda ||\beta||_0 \\
\beta^{\ast} &= \operatorname*{argmin}_{\beta} ||y - X\beta||_2^{2} + \lambda ||\beta||_1 \\
\beta^{\ast} &= \operatorname*{argmin}_{\beta} ||y - X\beta||_2^{2} + \lambda ||\beta||_2 \\
\end{align}
$$
Ideally, for weight sparsity and feature selection, L0 regression is the best optimization strategy. However, since L0 regression is not differentiable anywhere. We relax L0 regression to Lasso regression, and Lasso regression will also cause reasonable weight sparsity.
Group Lasso
Suppose the weights in $\beta$ could be grouped, the new weight vector becomes $\beta_G = \{ \beta^{(1)}, \beta^{(2)}, \cdots, \beta^{(m)} \}$. Each $\beta^{(l)}$ for $1 \leq l \leq m$ represents a group of weights from $\beta$.
We further group $X$ accordingly. We denote $X^{(l)}$ as the submatrix of $X$ with columns corresponding to the weights in $\beta^{(l)}$. The optimization problem becomes
$$
\begin{align}
\beta^{\ast} &= \operatorname*{argmin}_{\beta} \bigg|\bigg|y - \sum_{l=1}^{m} X^{(l)}\beta^{(l)}\bigg|\bigg|_2^{2} + \lambda \sum_{l=1}^{m} \sqrt{p_l} ||\beta^{(l)}||_2
\end{align}
$$
where $p_l$ represents the number of weights in $\beta^{(l)}$.
It should be noted that when there is only one group, i.e., $m=1$, Group Lasso is equivalent to Ridge; when each weight forms an independent group, i.e., $m=n$, Group Lasso becomes Lasso.
Sparsity
The most intuitive explanation to the sparsity caused by Lasso is that the non-differentiable corner along the axes in the Lasso $||\beta||_1$ are more likely to contact with the loss function $||y - X\beta||_2^{2}$. In Ridge regression, because it is differentiable everywhere in the Ridge $||\beta||_2$ , the chance of contact along the axes is extremely small.
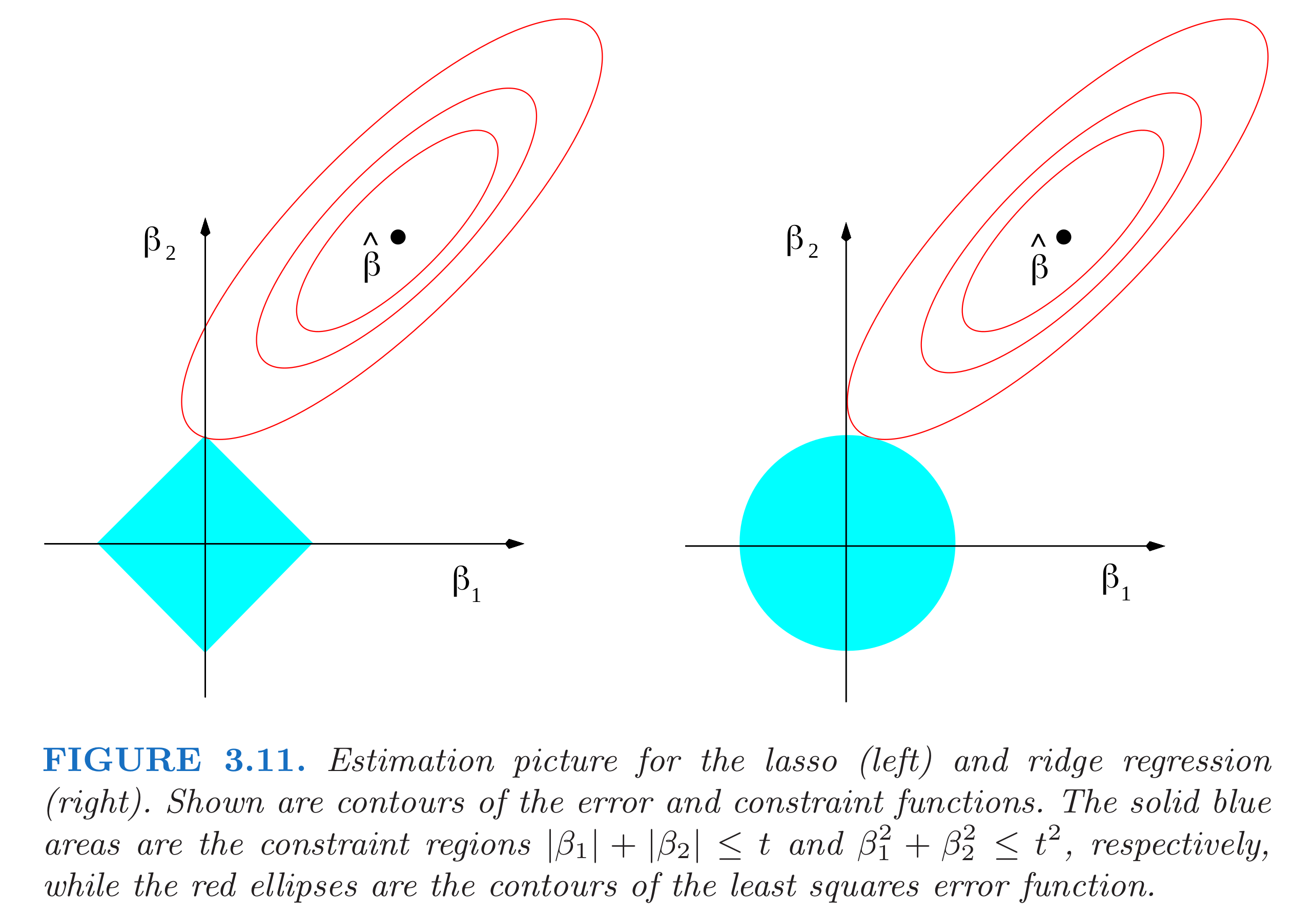
It should also be noted that the regularization strength $\lambda$ also matters. When $\lambda$ becomes larger, the size of Lasso $||\beta||_1$ will become smaller, and the chance of contact along the axes will become higher, thus the number of weights become zeros will become larger. On the contrary, When $\lambda$ becomes smaller, the size of Lasso $||\beta||_1$ will become larger, and the chance of contact along the axes will become smaller, thus the number of weights become zeros will become smaller. Please try to understand this and this is important.
Similarly, the original authors of the Group Lasso have provided the geometry for Lasso, Group Lasso, and Ridge on three dimensions. In Group Lasso in particular, the first two weights $\beta_{11}, \beta_{12}$ are in group and the third weight $\beta_2$ is in one group.
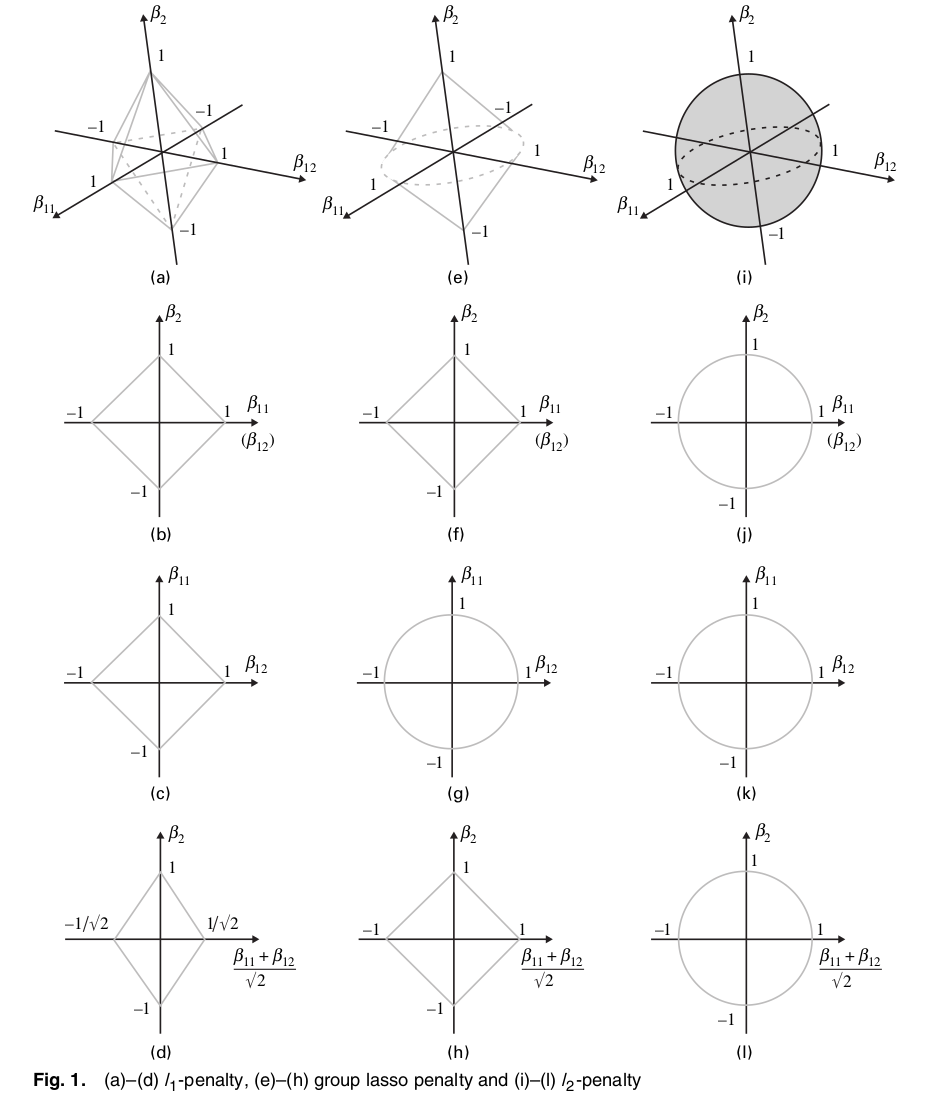
Because on the $\beta_{11}\beta_2$ plane or the $\beta_{12}\beta_2$ plane, there are still non-differentiable corners along the axes, there is a big chance of contact along the axes. Note that for the same regularization strength $\lambda$, the chance of contact along the axes for Group Lasso is smaller than that for Lasso but greater than that for Ridge.
References
Group Lasso