Intercausal Reasoning

Introduction

Intercausal reasoning, sometimes referred as intercausal inference, are important part of statistical reasoning or inference. “Explaining away” is a term that we often hear when we do intercausal reasoning.

In this blog post, I would like discuss what intercausal reasoning is, what explaining away is, and what the opposite of explaining away is, with examples.

Intercausal Inference

Suppose we have the following causal diagram. $X_1$ and $X_2$ are the causes and $Y$ is the effect.

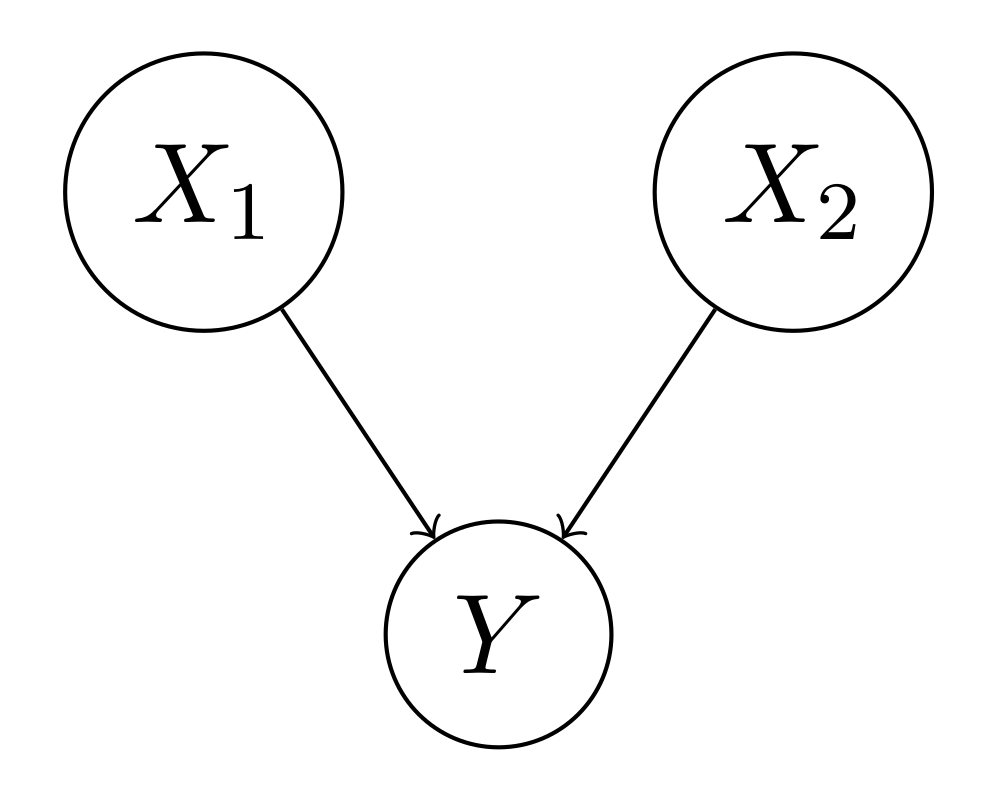
Given $X_1$ and/or $X_2$, computing $P(Y | X_1)$, $P(Y | X_2)$, and $P(Y | X_1, X_2)$ are predictive (or causal) reasoning, from cause to effect. Given $Y$, computing $P(X_1 | Y)$, $P(X_2 | Y)$, $P(X_1, X_2 | Y)$ are diagnostic (or evidential) reasoning, from effect to cause.

There is also another type of reasoning, called intercausal reasoning, that is reasoning between the causes with a common effect, in contrast with causal reasoning and evidential reasoning. Concretely, given $X_1$ and $Y$, compute $P(X_2 | X_1, Y)$, or given $X_2$ and $Y$, compute $P(X_1 | X_2, Y)$.

Note that although $X_1$ and $X_2$ could be completely independent variables, i.e., $P(X_1, X_2) \neq P(X_1) P(X_2)$, if $Y$ is known, $P(X_1 | Y)$ and $P(X_2 | Y)$ are no longer independent. Mathematically, $P(X_1, X_2 | Y) \neq P(X_1 | Y) P(X_2 | Y)$

A typical example of intercausal reasoning is explaining away. Let’s check what explaining away is with an example first, followed by an another example opposite to explaining away.

Noisy OR and Explaining Away

Explaining away is a common pattern of reasoning in which the confirmation of one cause of an observed or believed event reduces the need to invoke the alternative causes. Noisy OR is a good example of explaining away. We have the following distribution for a noisy OR distribution.

$X_1$	$X_2$	$Y$	$P$
0	0	0	0.20
0	0	1	0.05
1	0	0	0.05
1	0	1	0.20
0	1	0	0.05
0	1	1	0.20
1	1	0	0.05
1	1	1	0.20

$$
\begin{align}
P(X_1 = 1 | Y = 1) &= \frac{P(X_1 = 1, Y = 1)}{P(Y = 1)} \\
&= \frac{0.20 + 0.20}{0.05 + 0.20 + 0.20 + 0.20} \\
&= \frac{0.40}{0.65} \\
&\approx 0.615 \\
\end{align}
$$

$$
\begin{align}
P(X_1 = 1 | X_2 = 1, Y = 1) &= \frac{P(X_1 = 1, X_2 = 1, Y = 1)}{P(X_2 = 1, Y = 1)} \\
&= \frac{0.20}{0.20 + 0.20} \\
&= \frac{0.20}{0.40} \\
&= 0.500 \\
\end{align}
$$

We found that

$$
\begin{align}
P(X_1 = 1 | Y = 1) > P(X_1 = 1 | X_2 = 1, Y = 1)
\end{align}
$$

This means that given $Y = 1$, knowing $X_2 = 1$ explains away $X_1 = 1$, lowering the belief in $X_1 = 1$.

Noisy OR or OR distributions are common. For example, it could be that $X_1$ is whether it rained, $X_2$ is whether the sprinkler was on, and $Y$ is whether the grass was wet.

Noisy AND and Explaining “Close”

The opposite of explaining away can also occur. It is the pattern of reasoning in which the confirmation of one cause increases the belief in another. There is no official name for this pattern of reasoning. We might just call it explaining “close” in this article. Noisy AND is a good example of explaining close. We have the following distribution for a noisy AND distribution.

$X_1$	$X_2$	$Y$	$P$
0	0	0	0.20
0	0	1	0.05
1	0	0	0.20
1	0	1	0.05
0	1	0	0.20
0	1	1	0.05
1	1	0	0.05
1	1	1	0.20

$$
\begin{align}
P(X_1 = 1 | Y = 1) &= \frac{P(X_1 = 1, Y = 1)}{P(Y = 1)} \\
&= \frac{0.05 + 0.20}{0.05 + 0.05 + 0.05 + 0.20} \\
&= \frac{0.25}{0.35} \\
&\approx 0.714 \\
\end{align}
$$

$$
\begin{align}
P(X_1 = 1 | X_2 = 1, Y = 1) &= \frac{P(X_1 = 1, X_2 = 1, Y = 1)}{P(X_2 = 1, Y = 1)} \\
&= \frac{0.20}{0.05 + 0.20} \\
&= \frac{0.20}{0.25} \\
&= 0.800 \\
\end{align}
$$

We found that

$$
\begin{align}
P(X_1 = 1 | Y = 1) < P(X_1 = 1 | X_2 = 1, Y = 1)
\end{align}
$$

This means that given $Y = 1$, knowing $X_2 = 1$ explains close $X_1 = 1$, enhancing the belief in $X_1 = 1$.

Noisy AND or AND distributions are also common. For example, it could be that $X_1$ is whether John drank, $X_2$ is whether John drove, and $Y$ is whether John was killed in car crash.

References

• Explaining “Explaining Away”