Neural Network 1 x 1 Convolution Horizontal Fusion

Introduction

Neural network inference is the most critical topic for deep learning productization and commercialization. To execute neural network inference, kernels are invoked for neural network layers in order to compute the output tensors given the input tensors. Each kernel call will bring some overhead time. If many kernels were invoked for a neural network, the total overhead time might be very significant in a latency constraint system. So to achieve high throughput and low latency for neural network inference, the rule of thumb is to have fewer large kernel calls instead of many small kernel calls.

Given a pretrained neural network, all the layers have been fixed. In the worst scenario, each layer will invoke one kernel, and the total overhead time must be very significant for large neural networks. In order to reduce the number of kernel calls, we have to fuse the layers so that one kernel call does the computation for many neural network layers.

The neural network layer fusion could usually be categorized into horizontal layer fusion and vertical layer fusion. In my previous blog post “Neural Network Batch Normalization Fusion”, we have discussed the vertical layer fusion, including batch normalization fusion in particular. The vertical layer fusions are very common in neural network inference optimizations. However, the horizontal layer fusions are “rare”. In this blog post, I would like to discuss the horizontal layer fusion and more specifically the $1 \times 1$ convolutional horizontal layer fusion.

Inception Neural Networks

Neural networks, such as Google’s Inception neural networks, sometimes use branched convolutions given the an input tensor.

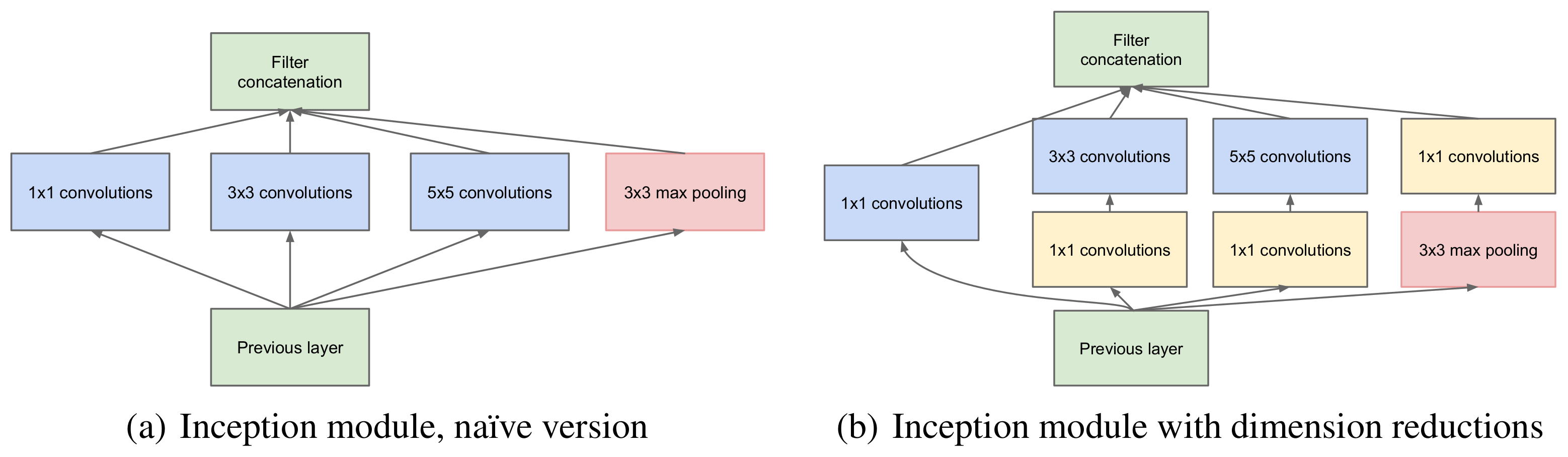
Note that the inception module (with dimension reduction) has four branches from a single input. Among three of the four branches, $1 \times 1$ convolutional layers directly consumes the same input. Without optimization, the three $1 \times 1$ convolutional layers will invoke three convolution kernel calls. With optimization, the three convolution layers calls could be fused into one layer horizontally, and thus only one convolution kernel call is invoked. Let’s see how we could fuse the $1 \times 1$ convolutional layers horizontally.

$1 \times 1$ Convolution Fusion

$1 \times 1$ convolution is actually equivalent to a linear layer.

Suppose $X \in \mathbb{R}^{N \times H \times W \times C}$ is the input tensor to the $1 \times 1$ convolutional layer, $W \in \mathbb{R}^{C \times 1 \times 1 \times C^{\prime}}$ is the weight parameter, and $b \in \mathbb{R}^{C^{\prime}}$ is the bias parameter, and $Y \in \mathbb{R}^{N \times H \times W \times C^{\prime}}$ is the output tensor from the convolutional layer, assuming stride is $1$.

$$
Y = X \ast W + b
$$

where $\ast$ is the convolutional operator.

The two middle $1$ dimensions in $W$ could be squeezed. So we define $W^{\prime} \in \mathbb{R}^{C \times C^{\prime}}$ as the squeezed version of the weight parameter $W$. So we have

$$
\begin{align}
Y &= X \ast W + b \\
&= X W^{\prime} + b
\end{align}
$$

Consider the $1 \times 1$ convolutions in the inception module. Suppose we have $k$ $1 \times 1$ convolutions for the input tensor $X \in \mathbb{R}^{N \times H \times W \times C}$, the weight parameters for the $1 \times 1$ convolutions are $W_1 \in \mathbb{R}^{C \times 1 \times 1 \times C^{\prime}_{1}}$, $W_2 \in \mathbb{R}^{C \times 1 \times 1 \times C^{\prime}_{2}}$, $\cdots$, $W_k \in \mathbb{R}^{C \times 1 \times 1 \times C^{\prime}_{k}}$, and the $1 \times 1$ convolutions in the inception modules do not have bias terms, i.e., the bias parameters $b_1 = 0$, $b_2 = 0$, $\cdots$, $b_k = 0$. So the output tensor $Y_i \in \mathbb{R}^{N \times H \times W \times C^{\prime}_{i}}$, for all $i \in [1, k]$. We define the squeezed versions of the weight parameters, $W^{\prime}_{1} \in \mathbb{R}^{C \times C^{\prime}_{1}}$, $W^{\prime}_{2} \in \mathbb{R}^{C \times C^{\prime}_{2}}$, $\cdots$, $W^{\prime}_{k} \in \mathbb{R}^{C \times C^{\prime}_{k}}$. Concretely,

$$
\begin{align}
Y_i &= X \ast W_i + b_i \\
&= X \ast W_i \\
&= X W^{\prime}_i \\
\end{align}
$$

Now let’s start the horizontal layer fusion optimization. We define a new matrix $W^{\ast} \in \mathbb{R}^{C \times (\sum_{i=1}^{k} C^{\prime}_{i})}$, which is a horizontal concatenation of all the squeezed versions of the weight parameters, i.e.,

$$
W^{\ast} = [W^{\prime}_{1}, W^{\prime}_{2}, \cdots, W^{\prime}_{k}]
$$

We further define another new matrix $Y^{\ast} \in \mathbb{R}^{N \times H \times W \times (\sum_{i=1}^{k} C^{\prime}_{i})}$, which is a horizontal concatenation of all the output tensors, i.e.,

$$
Y^{\ast} = [Y^{\prime}_{1}, Y^{\prime}_{2}, \cdots, Y^{\prime}_{k}]
$$

The $k$ $1 \times 1$ convolutions for the input tensor $X$ could be equivalently replaced by one single linear layer (matrix multiplication).

$$
\begin{align}
Y^{\ast} &= [Y^{\prime}_{1}, Y^{\prime}_{2}, \cdots, Y^{\prime}_{k}] \\
&= [X W^{\prime}_{1}, X W^{\prime}_{2}, \cdots, X W^{\prime}_{k}] \\
&= X[W^{\prime}_{1}, W^{\prime}_{2}, \cdots, W^{\prime}_{k}] \\
&= XW^{\ast} \\
\end{align}
$$

In order to obtain each $Y_i$ specifically, we could use the efficient slicing. That is to say,

$$
Y_i = Y^{\ast}_{:,:,:,\sum_{j=1}^{i-1} C^{\prime}_{j}: \sum_{j=1}^{i} C^{\prime}_{j}}
$$

More General Convolution Fusion?

Theoretically, all the convolutions could be equivalently transformed to matrix multiplications. However, except $1 \times 1$ convolutions, transforming all the other convolutions to matrix multiplications turns out to be computational and memory expensive, not to mention layer fusions. That is why usually only $1 \times 1$ convolutional horizontal layer fusions are seen.

Conclusions

We have mathematically derived the validness of fusing several $1 \times 1$ convolutional layer horizontally into a single linear layer.