Neural Radiance Fields
Introduction
Based on the volume rendering technique, if the color $c$ and opacity $\tau$ of the infinitesimal particles along the ray are known, the observed color of the ray casting on the 2D image can be estimated. If we could model the color and opacity of an infinitesimal particle in a volume as a function of constant time, the volume can be rendered at any viewpoint efficiently.
Neural Radiance Fields (NeRF) is a technique that represents a 3D scene as a continuous function that maps the 3D spatial location and 2D viewing direction to the emitted radiance and opacity. The function is represented by a neural network that is trained on a set of images of the scene taken from different viewpoints.
In this blog post, we will discuss the NeRF technique.
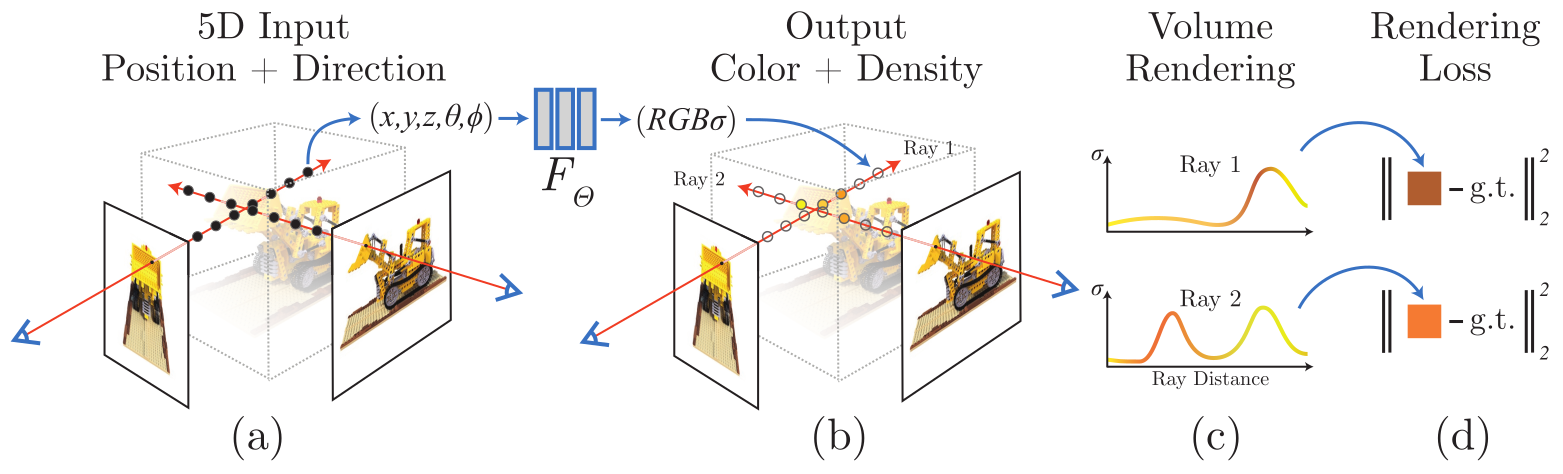
Neural Radiance Fields
The differentiable neural radiance field neural network $F_{\Theta}$ consumes a 3D location $\mathbf{x} = (x, y, z)$ in the volume and a viewing direction $\mathbf{d} = (\theta, \phi)$ and outputs the emitted color $\mathbf{c} = (r, g, b)$ and the volume density $\sigma$, i.e., $(\mathbf{c}, \sigma) = F_{\Theta}(\mathbf{x}, \mathbf{d})$. Given a ray $\mathbf{r} = (\mathbf{o}, \mathbf{d})$, the rendered color of the ray casting on the 2D image can be estimated by integrating the emitted color and opacity along the ray using the differentiable volume rendering technique. Therefore, the volume rendering function is differentiable end-to-end and the parameterized neural network can be trained using the gradient descent algorithm.
Given a set of images of the scene taken from different viewpoints, the neural network is trained to minimize the error between the observed color on the 2D image and the estimated color of the ray casting on the 2D image.
Optimizating Neural Radiance Fields
The training of neural radiance field neural network seems to be straightforward. However, without some tricks, the quality of the neural network might not be ideal.

Positional Encoding
The differentiable neural radiance field neural network $F_{\Theta}$ can be reformulated as a composition of two functions $F_{\Theta} = F^{\prime}_{\Theta} \circ \gamma$, where $F^{\prime}_{\Theta}$ is a parameterized neural network and $\gamma$ is a positional encoding function that encodes the 3D location $\mathbf{x}$ and the viewing direction $\mathbf{d}$ using a Fourier feature encoding. The encoding is used to represent the spatial location and the viewing direction in the neural network. This is because neural networks are usually biased toward learning low-frequency encoding functions and the Fourier feature encoding can provide high-frequency features to the neural network directly which can potentially improve the resolution of the rendered image.
Concretely, the positional encoding function $\gamma$ is defined as
$$
\begin{align}
\gamma(\mathbf{v}) &= \left( \sin\left(2^{0} \pi \mathbf{v}\right), \cos\left(2^{0} \pi \mathbf{v}\right), \ldots, \sin\left(2^{L-1} \pi \mathbf{v}\right), \cos\left(2^{L-1} \pi \mathbf{v}\right) \right) \\
\end{align}
$$
where the vector $\mathbf{v}$ are usually normalized or constructed to be in the range of $[-1, 1]$ and $L$ is the number of arbitrary features selected for encoding.
The neural radiance field function becomes
$$
\begin{align}
(\mathbf{c}, \sigma) &= F_{\Theta}(\mathbf{x}, \mathbf{d}) \\
&= (F^{\prime}_{\Theta} \circ \gamma) (\mathbf{x}, \mathbf{d}) \\
&= F^{\prime}_{\Theta} (\gamma(\mathbf{x}, \mathbf{d})) \\
&= F^{\prime}_{\Theta}(\gamma(\mathbf{x}), \gamma(\mathbf{d})) \\
\end{align}
$$
Hierarchical Volume Sampling
Because the quality of volume rendering is sensitive to the sampling of the volume, if the (sparse) sampling locations along the ray is not informative, the rendered image might be noisy. Therefore, the quality of the neural network trained also depends on the volume sampling locations.
To improve the quality of the neural radiance field neural network, a hierarchical volume sampling and neural network training strategy is proposed.
Concretely, an uninformative sampling strategy is used to sample the volume and a coarse neural network is firstly trained. At each sampling location, the volume density $\sigma$ can be predicted from the neural network and weight of the sampling location $T_{\mathbf{r}}(s_i) \left( 1 - \exp\left(- \sigma(\mathbf{r}(s_i)) \Delta s_i\right) \right)$ can be computed. Based on the weights of the color contribution, the sampling locations can be refined by a more informative sampling strategy and a fine neural network can be trained.
References
Neural Radiance Fields