Simple Proof To The Container With Most Water Problem

Introduction

One of my friends asked me a question on a popular LeetCode problem Container With Most Water Problem. He told me that the solution algorithm is easy to implement and he sort of has an intuition to the solution. However, he was not able to prove the correctness of the algorithm, neither did he understand the complicated explanation or proof in the discussion section. So he asked me if I could give a (simple) proof which he could understand easily.

After looking at the problem, I was able to come up with the solution algorithm using the two pointers based on my gut feelings, which is almost the same as the solution on the official LeetCode website. However, it took me hours on brain-twisting proofs before I finally came up with a simple proof.

In this blog post, I am going to introduce the problem and the two-pointer algorithm solution to the problem first for completeness. Then I will give a simple proof for algorithm correctness.

Problem

Description

Given $n$ non-negative integers $a_1, a_2, \cdots, a_n$, where each represents a point at coordinate $(i, a_i)$. $n$ vertical lines are drawn such that the two endpoints of line $i$ is at $(i, a_i)$ and $(i, 0)$. Find two lines, which together with $x$-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and $n$ is at least 2.

Example

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

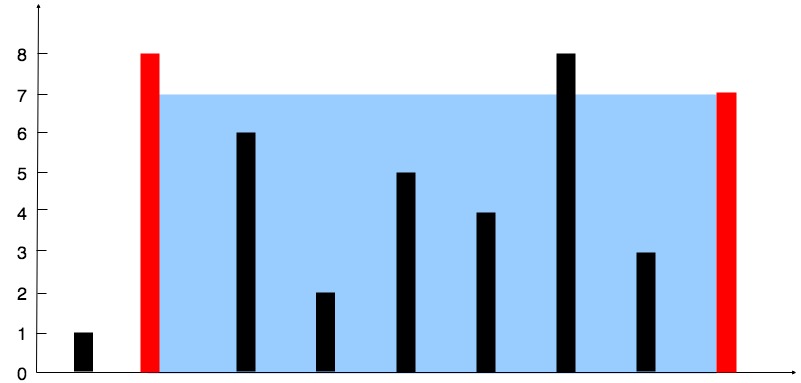
Solutions

Brute Force Solution

The brute force solution is simple. It took $O(n^2)$ runtime and $O(1)$ space since the combination of container walls is $O(n^2)$. I am not going to show the solution here.

Two Pointer Approach

The volume of the container is computed as $S(i,j)=(j-i)\min(a_i, a_j)$. We put the left pointer at the first wall and put the right pointer at the last wall respectively. In each step, if the left wall is shorter than the right wall, we move the left pointer right by one, and similarly, if the right wall is shorter than the left wall, we move the right pointer left by one, until the left wall meets the right wall. In each step, we also compute the volume of the container, keep the maximum volume and optionally the corresponding container wall indices.

The gut feeling is that we are decreasing the value of $(j-i)$ after each step, using the above method would find larger $\min(a_i, a_j)$, and therefore a possible candidate for maximum volume. It would only need to compute the area at most $n-1$ times (you could do some simple wall height comparisons to avoid area computation sometimes if you want to further optimize the algorithm), while the brute force combination needs to compute the area $\frac{n(n-1)}{2}$ times. Therefore, the asymptotic runtime complexity is $O(n)$ and the space complexity is also $O(1)$.

I have attached my simple implementation using C++ to the above algorithm.

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0;
        int j = height.size() - 1;
        int maxVol = -1;
        int vol;
        while (i < j)
        {
            if (height[i] < height[j])
            {
                vol = (j - i) * height[i];
                if (vol > maxVol)
                {
                    maxVol = vol;
                }
                i ++;
            }
            else
            {
                vol = (j - i) * height[j];
                if (vol > maxVol)
                {
                    maxVol = vol;
                }
                j --;
            }
        }
        return maxVol;
    }
};

While it passed all the tests on the LeetCode grading system, how do we know this algorithm always gives the correct result? We only computed the area $n-1$ times and found the maximum of them. How do we know the rest of the combinations, which have not been computed in the above algorithm, do not have the area larger than this particular maximum?

Proof

Proof by Elimination

We have an array of $a_1, a_2, \cdots, a_n$, without loss of generality, we assume $a_1 \leq a_n$, then $\min(a_1, a_n) = a_1$.

In the first iteration, we put the left pointer at $1$, and the right pointer at index $n$.

This means that the area of container $S(1,2), S(1,3), \cdots, S(1,n) \leq S(1,n)$. This is because $\min(a_1, a_2), \min(a_1, a_3), \cdots, \min(a_1, a_n) \leq \min(a_1, a_n)$. Note that $\min(a_1, a_j) \leq a_1$ for $1 < j \leq n$, and $\min(a_1, a_n) = a_1$.

In the first iteration, we eliminated $n-2$ candidates, $(1,j)$ for $1 < j < n$, for maximum container volume.

In the second iteration, the left pointer is at $2$, and the right pointer is at index $n$. Without further loss of generality, we assume $a_2 > a_n$, then $\min(a_2, a_n) = a_n$.

This means that the area of container $S(2,n), S(3,n), \cdots, S(n-1,n) \leq S(2,n)$. This is because $\min(a_2, a_n), \min(a_3, a_n), \cdots, \min(a_{n-1}, a_n) \leq \min(a_2, a_n)$. Note that $\min(a_i, a_n) \leq a_n$ for $2 \leq i < n-1$ and $\min(a_2, a_n) = a_n$.

In the second iteration, we eliminated $n-3$ candidates, $(i,n)$ for $1 < i < n-1$, for maximum container volume.

We iterate until the left wall and the right wall meet. This final iteration eliminates zero candidates.

The total number of iterations is $n-1$.

Taken together, we have eliminated $(n-2) + (n-3) + \cdots + 1 + 0 = \frac{(n-1)(n-2)}{2}$ combinations and measured the area of $n-1$ containers. Note that $\frac{(n-1)(n-2)}{2} + (n-1)$ is exactly $\frac{n(n-1)}{2}$. There is no overlap between the eliminated candidates in each iteration because the eliminated candidates in each iteration would always have a unique index. In our case, in the first iteration, the unique index is 1 on the left, and it would not show up in the later eliminated candidates. In the second iteration, the unique index is $n$ on the right, and so on.

The whole proof is very simple, and it does not actually care which side of the container wall is higher or lower. Other proofs, which might be correct, are very likely to be brain-twisting.

Final Remarks

I personally never thought highly of those coding questions. Because some problems are actually very hard or tricky to solve and prove theoretically. Taking this problem as an example, you might be able to come up with a solution based on your gut feelings in a 45-minute coding interview. However, you did not actually know whether the algorithm you were using is correct or not, even if your implementation has passed all the test examples.

This reminded me of a mathematics examination I attended in high school many years ago. There was a multiple-choice question on the test paper. “If you cut a cube of side length $a$ with a knife to get a hexagon plain. What is the largest area of the plain possible?” It gave me several options to choose from. I was stumped by the question, which was at the beginning of the test paper. Later because of this, I did not perform very well in that particular examination.

After the exam, I discussed it with my classmates. They all thought cutting in the middle of the sides and getting a regular hexagon gives you the largest area. When I asked them why, holy shit nobody knew. When the teacher discussed the test paper in the class, she skipped this question because she thought the answer was too easy and straightforward, and nobody except me lost the points in that particular problem. However, when I asked, she did not know the proof either.

I was frustrated. Later I spent several hours to write a formal proof for this and showed the proof to the teacher. The regular hexagon does give you the largest area in that particular problem. But only I knew why that was the case in the entire class, and I was the only person in the class who did not get the points for that particular problem in the test paper which everybody else considered it easy.

Conclusions

A right attitude toward the problem is more important than getting a correct solution to it.