Variable Elimination Algorithm

Introduction

Variable elimination algorithm is the most fundamental algorithm for probabilistic graphic model inference. Depending on the variable elimination order, the computation cost of variable elimination could unaffordable.

In this blog post, I would mainly like to discuss the complexity analysis of the variable elimination algorithm.

Variable Elimination

Variable elimination is necessary for the inference of probabilistic graphic models with discrete variables. For example, if we have a Bayesian network consisting of three variables $A, B, C$. The conditional probability distributions known are $P(A)$, $P(B | A)$, and $P(C | A, B)$. Given the probability distribution $P(A, B, C) = P(A) P(B | A) P(C | A, B)$, We would like to compute the probability distribution for $P(C)$. This will require eliminating the variables $A$ and $B$ from the probability distributions.

Variable Elimination Algorithm

Eliminate variable $Z$ from a set of factors $\Phi$, where $\Phi= \{ \phi_1, \phi_2, \cdots\}$. We define the factor subset

$$
\Phi^{\prime} = {\phi_i \in \Phi: Z \in \text{Scope}(\phi_i)}.
$$

where $Z \in \text{Scope}(\phi_i)$ means the factor $\phi_i$ contains variable $Z$.

The variable elimination (algorithm) does multiplication and summation for factor product and marginalization, respectively.

$$
\begin{gather}
\psi = \prod_{\phi_i \in \Phi^{\prime}}^{} \phi_i \\
\tau = \sum_{Z}^{} \psi \\
\end{gather}
$$

Notice that if all the variables are discrete variables, all the factors and factor products can just be represented as factor or probability tables.

If there are multiple variables to eliminate, we will have to eliminate the variables one by one for each step. Suppose at the elimination step $k$ we are going to eliminate variable $Z$, the factor product and marginalization for the variable elimination could be expressed as

$$
\begin{gather}
\psi_k(\mathbf{X}_k) = \prod_{i=1}^{m_k} \phi_i \\
\tau_k(\mathbf{X}_k - \{ Z \}) = \sum_{Z}^{} \psi_k(\mathbf{X}_k) \\
\end{gather}
$$

where the variables involved in the factor product are $\mathbf{X}_k = \{ X_1, X_2, \cdots \}$, and $m_k$ is the number of factors whose scope contains variable $Z$.

Variable Elimination Algorithm Complexity

Suppose all the variables are discrete variables and none of the variables have been observed, let’s analyze the complexity of the variable elimination algorithm.

We first denote

$$
N_k = | \text{Val}(\mathbf{X}_k) |
$$

For example, if $\mathbf{X}_k = \{X_1, X_2\}$, $X_1 \in \{1,2,3\}$, $X_2 \in \{0,1\}$, then,

$$
\text{Val}(\mathbf{X}_k) = \big\{(1,0),(1,1),(2,0),(2,1),(3,0),(3,1)\big\}
$$

and $N_k = | \text{Val}(\mathbf{X}_k) | = 3 \times 2 = 6$.

We then look at the factor product step, which is just computing the factor table for $\psi_k(\mathbf{X}_k)$ from the factor tables for $\phi_1, \phi_2, \cdots, \phi_{m_k}$.

The factor table for $\psi_k(\mathbf{X}_k)$ consists of $N_k$ rows. To compute each row from the factor table for $\psi_k(\mathbf{X}_k)$, we need to pick one row from the factor table for each of $\phi_1, \phi_2, \cdots, \phi_{m_k}$, and multiply the factor values together. There are totally $m_k - 1$ multiplications to do for one row. Therefore, the factor product step takes $N_k (m_k - 1)$ multiplications. Using big-O notation, the complexity is $O\big(N_k (m_k - 1)\big)$.

We then look at the factor product step, which is just computing the factor table for $\tau_k(\mathbf{X}_k - { Z })$ from the factor table for $\psi_k(\mathbf{X}_k)$. The factor table for $\tau_k(\mathbf{X}_k - { Z })$ consists of $\frac{| \text{Val}(\mathbf{X}_k) |}{| \text{Val}(Z) |}$ rows. To compute each row from the factor table for $\tau_k(\mathbf{X}_k - { Z })$, we need to pick $| \text{Val}(Z) |$ rows from the factor table for $\psi_k(\mathbf{X}_k)$, and add the factor values together. There are totally $| \text{Val}(Z) | - 1$ additions to do for one row. Therefore, the marginalization step takes $\frac{| \text{Val}(\mathbf{X}_k) |}{| \text{Val}(Z) |} (| \text{Val}(Z) | - 1)$ additions. Notice that

$$
\begin{align}
\frac{| \text{Val}(\mathbf{X}_k) |}{| \text{Val}(Z) |} (| \text{Val}(Z) | - 1) &= \frac{| \text{Val}(\mathbf{X}_k) |}{| \text{Val}(Z) |} | \text{Val}(Z) |- \frac{| \text{Val}(\mathbf{X}_k) |}{| \text{Val}(Z) |} \\
&= | \text{Val}(\mathbf{X}_k) |- \frac{| \text{Val}(\mathbf{X}_k) |}{| \text{Val}(Z) |} \\
&= N_k- \frac{N_k}{| \text{Val}(Z) |} \\
\end{align}
$$

In the “best scenario” where $Z$ is a binary variable, we still need to perform $\frac{N_k}{2}$ additions. So we can usually say the marginalization step takes $\sim N_k$ additions. Using big-O notation, the complexity is $O(N_k)$.

Now that we have analyzed the complexity for one single step, i.e., eliminating one variable, in the algorithm, we need to further analyze the complexity for eliminating multiple variables in the network. Suppose at the first step, we have $m_1 = m$ factors and there are $n$ variables, for Bayesian networks, $m \leq n$, and for Markov networks, $m$ can be much larger than $n$. At each elimination step, we will generate one new factor $\tau_k$. Because there are $n$ variables, there can be at most $n$ elimination steps.

Here we denote that the total number of factors that ever exist during variable elimination, the original factors and the new factors generated from marginalization, is $m^{\ast}$. We must have $m^{\ast} \leq m + n$. We further denote $N$ is the size of the largest factor, i.e., the largest number of rows of a factor table, during variable elimination. Concretely,

$$
N = \max \big(N_1, N_2, \cdots \big)
$$

So the number of multiplications required to eliminate $k$ variables is

$$
\begin{align}
\sum_{i=1}^{k} N_k (m_k - 1) &\leq \sum_{i=1}^{k} N (m_k - 1) \\
&\leq N \sum_{i=1}^{k} (m_k - 1) \\
&\leq N \bigg( \Big( \sum_{i=1}^{k} m_k \Big) - k \bigg) \\
&\leq N \Big( \sum_{i=1}^{k} m_k \Big) \\
&\leq N m^{\ast} \\
\end{align}
$$

Note that $\sum_{i=1}^{k} m_k \leq m^{\ast}$ because each variable could only be eliminate once.

Similarly, the number of additions required to eliminate $k$ variables is at most

$$
\begin{align}
\sum_{i=1}^{k} N_k &\leq \sum_{i=1}^{k} N \\
&\leq k N \\
&\leq n N \\
\end{align}
$$

So the total complexity for the variable elimination algorithm is $O(N m^{\ast}) + O(n N)$. Because for Markov networks, usually $m^{\ast} \gg n$, we could just conclude that the total complexity for the variable elimination algorithm is $O(N m^{\ast})$.

Because $N = \max \big(N_1, N_2, \cdots \big)$, depending on the order of variables to be eliminated, $N$ could be dramatically different. $m^{\ast}$ is determined by the number of factors and the number of variables to eliminate before the variable elimination, thus the order of variables to be eliminated will not affect $m^{\ast}$. In addition, because

$$
\begin{align}
N_k &= | \text{Val}(\mathbf{X}_k) | \\
&= \prod_{i=1}^{| \mathbf{X}_k |} | \text{Val}(X_i) | \\
&\leq \prod_{i=1}^{| \mathbf{X}_k |} \max_{j \in [1,| \mathbf{X}_k |] }(| \text{Val}(X_j) |) \\
&= \bigg(\max_{j \in [1,| \mathbf{X}_k |] }\big(| \text{Val}(X_j) |\big) \bigg)^{| \mathbf{X}_k |} \\
\end{align}
$$

$N_k$ is polynomial with respect to $| \mathbf{X}_k |$. Therefore, choosing a good variable elimination order so that none of the $| \mathbf{X}_1 |, | \mathbf{X}_2 |, \cdots, | \mathbf{X}_k |$ are too large is the most critical thing to reduce computation complexity.

Here is an extreme example. We have $n+2$ variables $A, B_1, B_2, \cdots, B_n, C$ in the Bayesian network, and we want to eliminate the variables $A, B_1, B_2, \cdots, B_n$. All the factors for the Bayesian network are $\phi(\{A, B_1\})$, $\phi(\{A, B_2\})$, $\cdots$, $\phi(\{A, B_n\})$, $\phi(\{C, B_1\})$, $\phi(\{C, B_2\})$, $\cdots$, $\phi(\{C, B_n\})$.

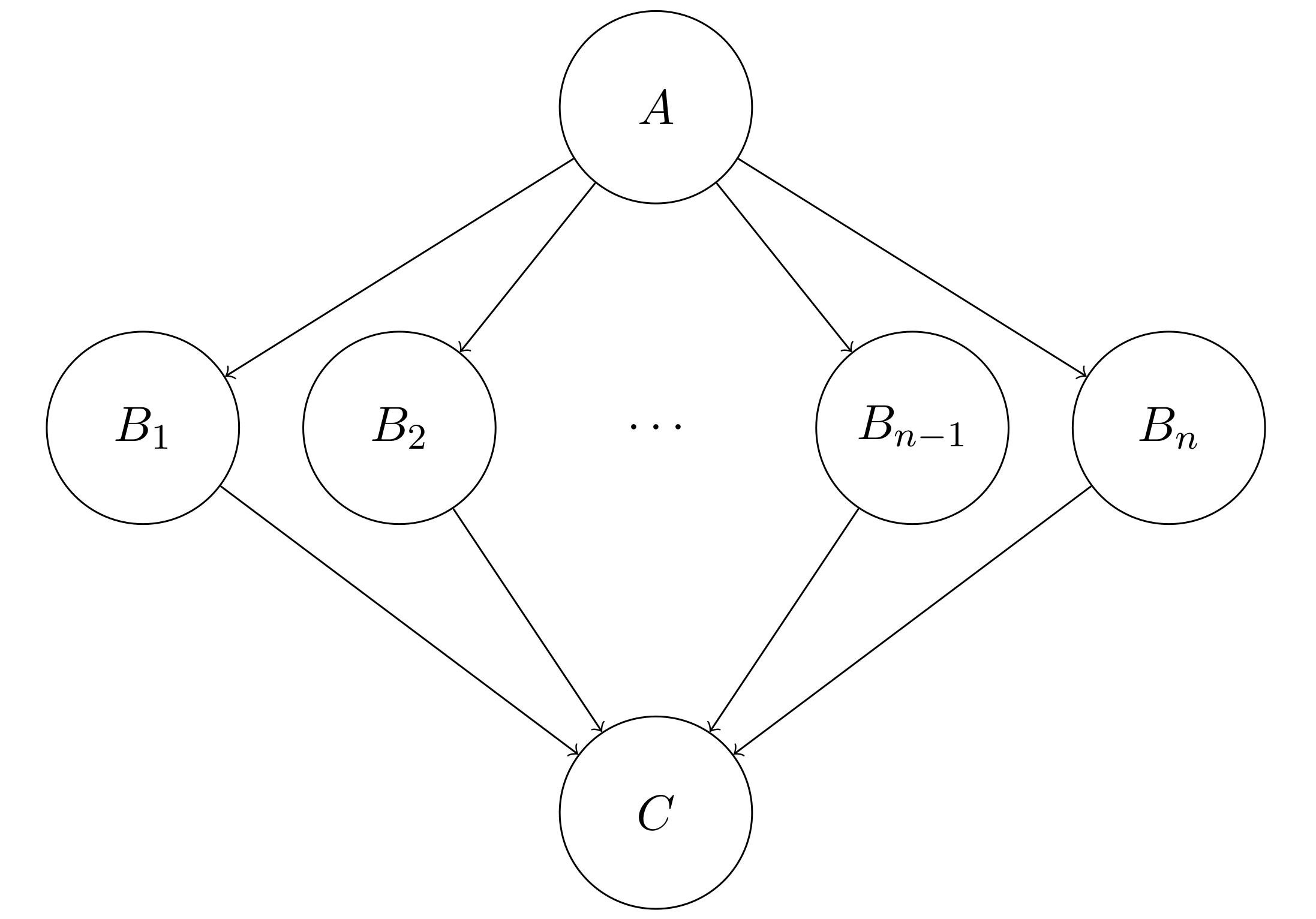
Let’s first consider the elimination order $A, B_1, B_2, \cdots, B_n$. For the very first step during elimination, we have to eliminate variable $A$, and we immediately found that $\mathbf{X}_1 = \{A, B_1, B_2, \cdots, B_n\}$ and $| \mathbf{X}_1 | = n + 1$. Therefore, even eliminating variable $A$ is intractable if $n$ is large.

How about the elimination order $B_1, B_2, \cdots, B_n, A$? We have $\mathbf{X}_1 = \{A, B_1, C\}$, $\mathbf{X}_2 = \{A, B_2, C\}$, $\cdots$, $\mathbf{X}_n = \{A, B_n, C\}$, and $\mathbf{X}_{n + 1} = \{A, C\}$. $\max(| \mathbf{X}_1 |, | \mathbf{X}_2 |, \cdots, | \mathbf{X}_{n+1} |) = 3$. Obviously, the elimination order $B_1, B_2, \cdots, B_n, A$ is much more feasible than the elimination order $A, B_1, B_2, \cdots, B_n$.

Therefore, the variable elimination algorithm complexity is $O(N m^{\ast})$ and $N$ will be significantly affected by the elimination order.

Variable Elimination Order

Determine the optimal variable elimination order is also NP-hard. There are a couple of heuristic variable elimination order determination algorithms which works well in practice, such as min-neighbors, min-weight, min-fill, etc. However, I will skip delve into this in this blog post.

References

• Variable Elimination Algorithm - Coursera
• Variable Elimination Algorithm