Hierarchical Softmax
Introduction
Because the word corpus of a language is usually very large, training a language model using the conventional softmax will take an extremely long time. In order to reduce the time for model training, people have invented some optimization algorithms, such as Noise Contrastive Estimation, to approximate the conventional softmax but run much faster.
In this blog post, instead of talking about a fast approximate optimization algorithm, I will talk about the non-approximate hierarchical softmax, which is a specialized softmax alternative that runs extremely fast with orchestration from human beings.
Methods
Conventional Softmax
In a model with parameters $\theta$, given some context $h$, to compute the probability of word $w$ given $h$ from the model,
$$
\begin{aligned}
P_{\theta}^{h}(w) &= \frac{\exp(s_{\theta}(w,h))}{Z_\theta^h} \\
&= \frac{u_{\theta}(w,h)}{Z_\theta^h}
\end{aligned}
$$
where $s_{\theta}(w,h)$ is usually called score or logit for word $w$ in the model, $u_{\theta}(w,h) = \exp(s_{\theta}(w,h))$, and $Z_\theta^h$ is the normalizer given context $h$ and it does not dependent on word $w$.
$$
\begin{aligned}
Z_\theta^h &= \sum\limits_{w^{\prime}} u_{\theta}(w^{\prime},h) \\
&= \sum\limits_{w^{\prime}} \exp(s_{\theta}(w^{\prime},h))
\end{aligned}
$$
Because the corpus is usually very large, computing $Z_\theta^h$ will usually take a very long time.
Hierarchical Softmax
Hierarchical softmax poses the question in a different way. Suppose we could construct a tree structure for the entire corpus, each leaf in the tree represents a word from the corpus. We traverse the tree to compute the probability of a word. The probability of each word will be the product of the probability of choosing the branch that is on the path from the root to the word.
For example, if we have the following tree to represent a corpus of words including Golf, Basketball, Football, Soccer, Piano, and Violin.
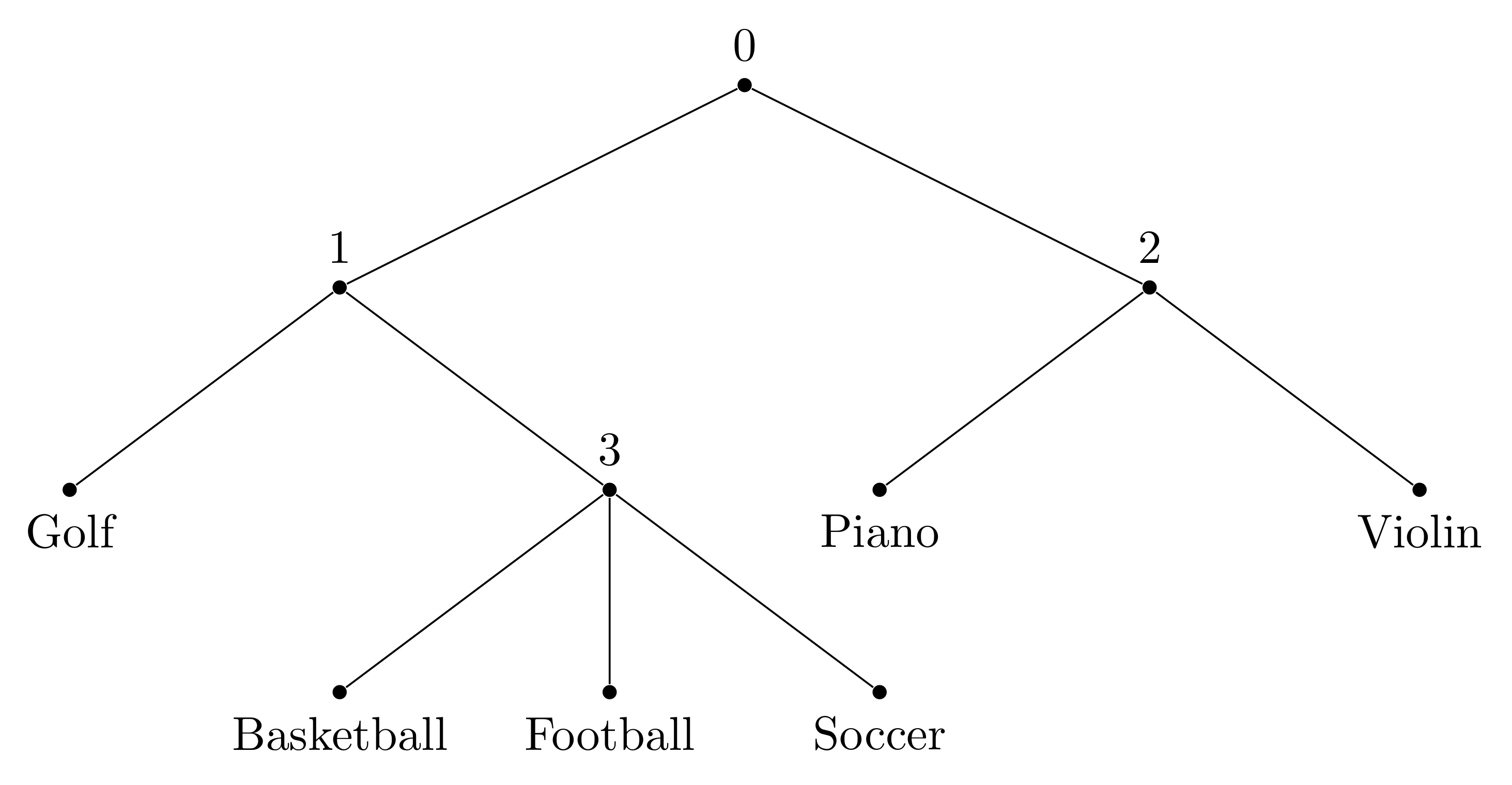
The probability of the word Football will be
$$
P_{\theta}^{h}(w=\text{Football}) = P_{\theta}^{h}(0\rightarrow1)P_{\theta}^{h}(1\rightarrow3)P_{\theta}^{h}(3\rightarrow\text{Football})
$$
Mathematically, each word $w$ can be reached by an appropriate path from the root of the tree. Let $n(w,j)$ be the $j$-th node on the path from the root to $w$, and let $L(w)$ be the length of this path. With these, $n(w,1)$ = root, and $n(w,L(w)) = w$, we have
$$
\begin{aligned}
P_{\theta}^{h}(w) = \prod_{j=1}^{L(w)-1} P_{\theta_j}^{h}(n(w,j) \rightarrow n(w,j+1))
\end{aligned}
$$
In this way, given a corpus, if we construct the tree appropriately, we could reduce the complexity of computing softmax from $O(N)$ to $O(\log N)$ where $N$ is the size of the corpus. For example, if we have a corpus of 10,000 words, we construct a two-layer hierarchical softmax, the first layer consists of 100 child nodes, each node in the first layer also consists of 100 child nodes. To compute the conventional softmax, we would need to compute $u_{\theta}(w^{\prime},h)$ 10,000 times. To compute the hierarchical softmax, we just have to compute $u_{\theta_1}(n^{\prime},h)$ 100 times in the first layer, and $u_{\theta_2}(w^{\prime},h)$ 100 times in the second layer, totalling 200 times!
Finally, the question is how to compute each $P_{\theta_j}^{h}(n(w,j) \rightarrow n(w,j+1))$ in practice. We assume the layer before projecting to softmax has size of $d$. For each edge $e$ in the tree, we denote the number of child nodes under the edge is $c(e)$. we would have a set of weights $W \in \mathbb{R}^{d \times c(e)}$ and biases $b \in \mathbb{R}^{c(e)}$.
In a model using conventional softmax, the number of weight parameters on the layer before softmax is $d \times N$. In a model using hierarchical softmax, the number of weight parameters on the layers before softmax is much more. The number of weight parameters on the final layer, taken together, is still $d \times N$. However, we would need additional parameters for the weights on the edge before the final layer in the tree.
To compute $P_{\theta_j}^{h}(n(w,j) \rightarrow n(w,j+1))$, we have a vector $v \in \mathbb{R}^{d}$ from the model, the weights are $W_{n(w,j) \rightarrow n(w,j+1)} \in \mathbb{R}^{d \times c(n(w,j) \rightarrow n(w,j+1))}$ and the bias are $b_{n(w,j) \rightarrow n(w,j+1)} \in \mathbb{R}^{c(n(w,j) \rightarrow n(w,j+1))}$. The resulting logit vector would be $vW_{n(w,j) \rightarrow n(w,j+1)} + b_{n(w,j) \rightarrow n(w,j+1)}$. Based on this logit vector which consists the logits for all the child nodes, we could compute easily the probability of choosing the node $n(w,j+1)$, which is $P_{\theta_j}^{h}(n(w,j) \rightarrow n(w,j+1))$, using a conventional softmax function.
Caveats
The model is highly biased by the structure of the corpus tree. With good trees constructed, the model would likely to be trained well. With bad trees, the model would probably never achieve very good performance.
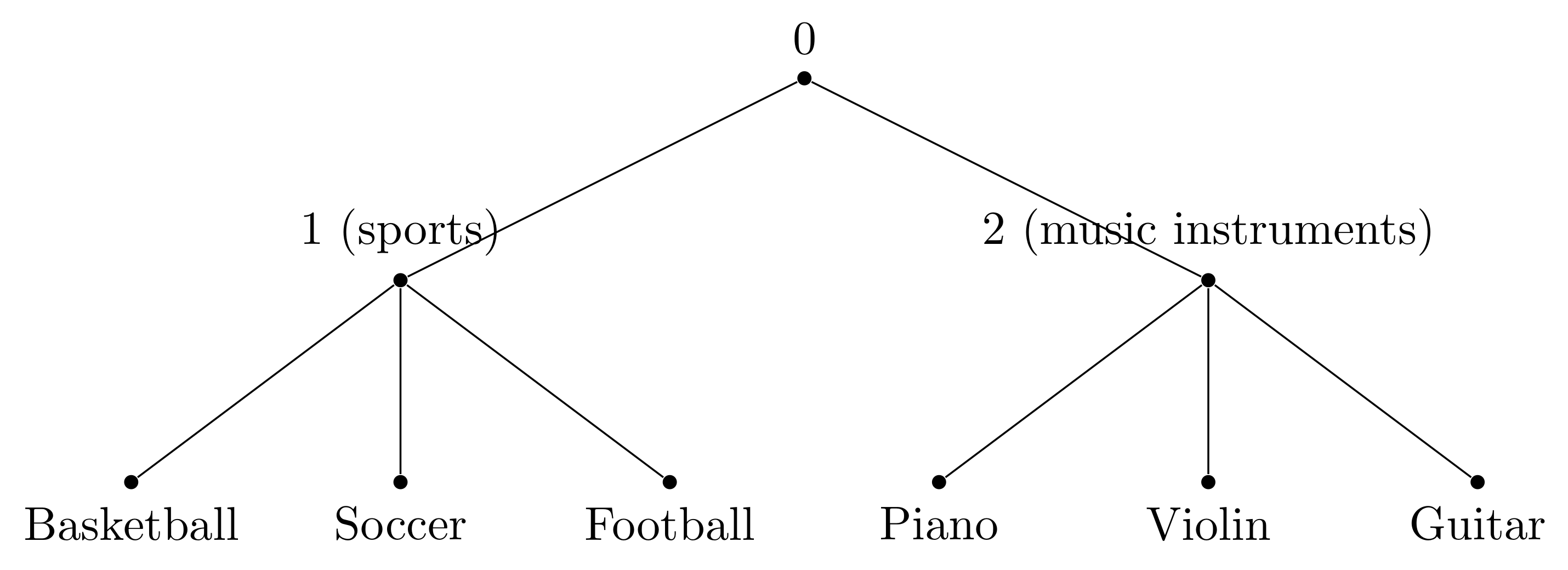
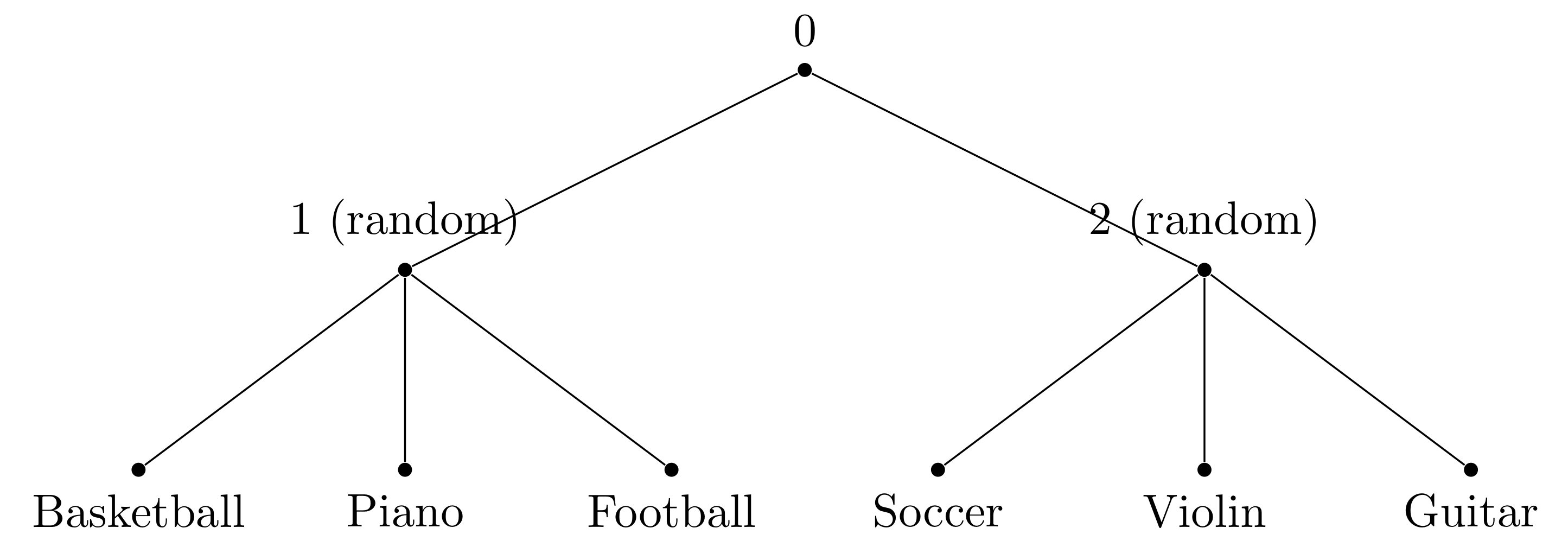
In the model using hierarchical softmax, we implicitly introduced additional labels for the words in each layer. If those labels “make sense” and the model could learn the label information in each layer, such kind of model could usually learn very well. On the contrary, it would just “confuse” the model. The example above shows a good tree and a bad tree for the corpus. On the good tree, all the words on the left branch are related to sports and all the words on the right branch are related to musical instruments. Given some context $h$, the model would first judge whether the word to be predicted is a word related to sports or musical instruments. Once it is determined, say, it is sports, it will then determine whether the word is Basketball, Soccer or Football. However, on the bad tree, because the “label” on the first layer is ambiguous, the model could hardly learn too useful information, and could not even determine which branch to go in the first layer during inference.
There are some methods to construct a relatively good tree, such as a binary huffman tree, but I am not going to elaborate on it here.
Conclusions
Hierarchical softmax is not an approximate optimization algorithm. It accelerates the optimization by adding human orchestrations which could be highly biased.
References
Hierarchical Softmax