Word2Vec Models Revisited

Introduction

The Word2Vec models proposed by Mikolov et al. in 2013, including the Continuous Bag-of-Words (CBOW) model and the Continuous Skip-Gram (Skip-Gram) model, are some of the earliest natural language processing models that could learn good vector representations for words. Although the word vector representations learned from these two models are no longer directly used in the state-of-the-art natural language processing models, such as Transformer and BERT, the basic ideas of the Word2Vec models are still affecting a lot of the latest natural language processing models.

In this blog post, I will go through what the CBOW model and the Skip-Gram model are, how they are trained, and how they have influenced the state-of-the-art models. Some of the math are interesting so it is very worth revisiting.

Word2Vec Models

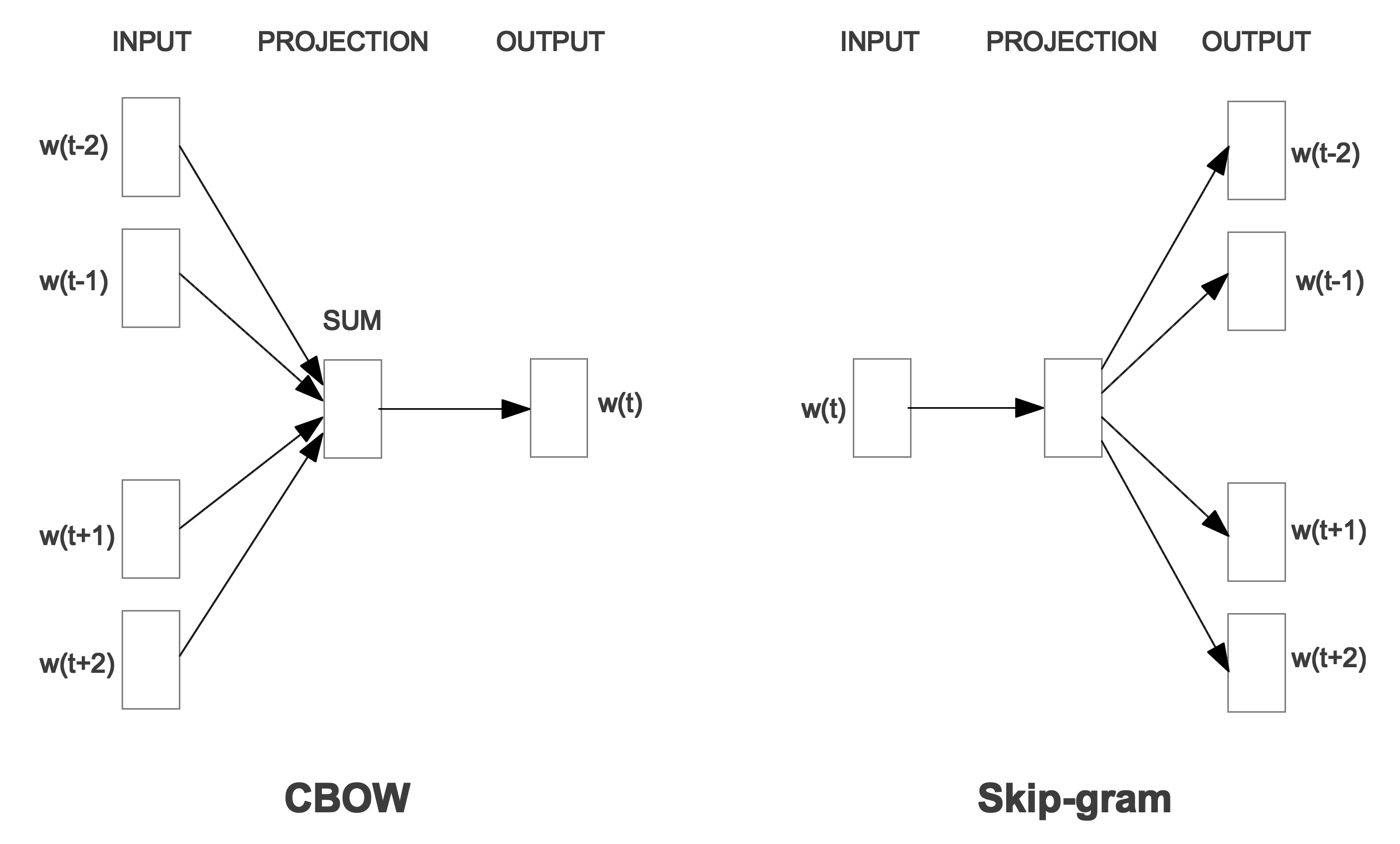
We will go over both the CBOW model and the Skip-Gram model, with emphasis on the Skip-Gram model. Probably due to the restriction of computation cost at that time, unlike a feed-forward neural network with at least one hidden layer, both the CBOW model and the Skip-Gram model did not have hidden layers at all.

Trainable Embedding Matrix

We first create a trainable embedding matrix $E \in \mathbb{R}^{n \times d}$, where $n$ is the number of words in the corpus and $d$ is the size of embedding vector for each word. Each row is an embedding vector for one unique word. During training, because we allow the values in the embedding vector to be trained, the back propagation will tune the values in the embedding matrix $E$.

CBOW Model

The CBOW model tries to predict the word given its past words and future words. For example, suppose we have four words, two past words “I” and “like”, and two future words “computer” and “games”, we would like to predict the words in the middle. In this case, the word is likely to be “playing”. It should be noted that the order of the input words does not matter in the model. You could imagine, in this case, the model is taking four words as inputs and generates only one output. The embeddings of the four words were projected to four vectors using a shared weight matrix (and possibly a shared bias term), and the four vectors were averaged and the softmax were computed for the predicted word distribution.

More formally, we have a weight matrix $W \in \mathbb{R}^{n \times d}$, and a bias term $b \in \mathbb{R}^{n}$. We have the embeddings for the four words $v_{t-2}$, $v_{t-1}$, $v_{t+1}$, $v_{t+2}$ from the embedding matrix $E$. Each vector $v \in \mathbb{R}^{d}$. Note that all the vectors in the article are column vectors. The logit vector $o_{t} \in \mathbb{R}^{n}$ used for computing softmax is as follows.

$$
\begin{aligned}
o_{t} &= \frac{1}{4} \big[ (W v_{t-2} + b) + (W v_{t-1} + b) + (W v_{t+1} + b) + (W v_{t+2} + b) \big] \\
&= \frac{1}{4} W (v_{t-2} + v_{t-1} + v_{t+1} + v_{t+2}) + b
\end{aligned}
$$

If we set $v_{t}^{\prime}$ to the average of the input word embeddings, it is equivalent to convert the CBOW model to a model which takes only one input and generates one output.

$$
\begin{aligned}
o_{t} &= \frac{1}{4} W (v_{t-2} + v_{t-1} + v_{t+1} + v_{t+2}) + b \\
&= W v_{t}^{\prime} + b
\end{aligned}
$$

During training, the model tries to maximize the probability of predicting the current word based on the surrounding context.

In summary, to design the architecture of the CBOW model, as we have just discussed above, you can design a model which takes the average of the input embeddings as the only input and generates one output, or you can take multiple input embeddings as inputs, average the projected vectors of them in the model, and generates one output.

Skip-Gram Model

The Skip-Gram model, opposite to the CBOW model, tries to predict the past words and future words given the current words. For example, suppose we have the word “playing”, we would like to predict the four words around it. In this case, the surrounding words are likely to be “I”, “like”, “computer”, “games”. It should be noted that the order of the output words does not matter in the model.

The diagram of the Skip-Gram model looks daunting. It looks like the model is taking one word as input and generates four outputs. This is misleading. In practice, the Skip-Gram model only takes one input and generates one output. Given an example, “I like playing computer games”, here is how we prepare the training data. We would have four input and label tuples for one example, including (“playing”, “I”), (“playing”, “like”), (“playing”, “computer”), (“playing”, “games”). These four examples were fed in a same batch to the neural network for training. The embedding of the input word was projected to one vector using a weight matrix (and possibly a bias term), the projected vector would be computed for softmax for the predicted word distribution.

More formally, we have a weight matrix $W \in \mathbb{R}^{n \times d}$, and a bias term $b \in \mathbb{R}^{n}$. We have the embedding for the current word $v_{t}$ from the embedding matrix $E$. The logit vectors $o_{t-2}$, $o_{t-1}$, $o_{t+1}$, $o_{t+2}$ used for computing softmax are as follows. Each vector $o \in \mathbb{R}^{n}$.

$$
\begin{aligned}
o_{t-2} &= W v_{t} + b \\
o_{t-1} &= W v_{t} + b \\
o_{t+1} &= W v_{t} + b \\
o_{t+2} &= W v_{t} + b \\
\end{aligned}
$$

During training, the model tries to maximize the probability of predicting one of the surrounding words based on the current word.

The values of $o_{t-2}$, $o_{t-1}$, $o_{t+1}$, $o_{t+2}$ in the forward propagation are exactly the same because the four training examples have the exact same input. But the label for the four training examples is different. Mathematically, it is equivalent to having “playing” as input, and use a non-one-hot probability vector where the probability of “I”, “like”, “computer”, “games” are 0.25 respectively as the labels for softmax. The proof is given in the appendix chapter. So this time, in this case, instead of feeding a batch of size 4, we only need to feed a batch of size 1, to the model.

In summary, to design the architecture of the Skip-Gram model, as we have just discussed above, you can design a model that takes the input word embedding as the input and generates one output. During training, you can feed multiple examples with the same input word but different labels, or you can feed one example with the input word and a probability vector representing the probabilities of the surrounding labels.

Optimization Methods

Because it is a language model, the cost of computing softmax is extremely expensive. So the original authors used the following optimization methods instead.

Hierarchical Softmax

Instead of computing the full softmax, we could input some prior knowledge to the hierarchy of the classes, build tree structure of the labels in the computation graph, and reduce the computation cost by selectively choosing the path for optimization. I have a detailed tutorial on this topic. If you are interested, please read my article “Hierarchical Softmax”.

Noise Contrastive Estimation

Essentially, we introduced a noise distribution, and convert the multi-class classification problems to binary classification problems distinguishing if the sampled word is from the original dataset distribution or noise distribution. I have a sophisticated tutorial with all the mathematics derivations on this topic. If you are interested, please read my article “Noise Contrastive Estimation”.

Negative Sampling

The original authors also proposed Negative Sampling to “approximate” Noise Contrastive Estimation so that the computation is even faster. In my opinion, the complexity of Negative Sampling is asymptotically the same as Noise Contrastive Estimation, and there should be no need to use it anymore nowadays. What’s more, mathematically Negative Sampling deviates Noise Contrastive Estimation. It no longer does maximum likelihood estimation, while Noise Contrastive Estimation still does maximum likelihood estimation if the noise to data ratio is high. This probably restricts Negative Sampling to be only useful for embeddings training, but not for other machine learning problems. Here I will show some quick explanations to Negative Sampling using mathematics based on the Noise Contrastive Estimation. To fully understand it, I suggest the readers going through my “Noise Contrastive Estimation” first.

Let’s see what the optimization objective function is for Negative Sampling. In the paper, the authors defined it as

$$
J = \log \sigma(v_{w_O}^{\prime \top} v_{w_I}) + \sum_{i=1}^{k} \mathbb{E}_{w_i \sim P_n(w)}\big[\log (-v_{w_i}^{\prime \top} v_{w_I}) \big]
$$

In my opinion, this expression is mathematically incorrect, I believe what they meant is

$$
J = \log \sigma(v_{w_O}^{\prime \top} v_{w_I}) + k \mathbb{E}_{w_i \sim P_n(w)}\big[\log (-v_{w_i}^{\prime \top} v_{w_I}) \big]
$$

To estimate the expected value, we sample $k$ words from the noise distribution.

$$
\mathbb{E}_{w_i \sim P_n(w)}\big[ \log (-v_{w_i}^{\prime \top} v_{w_I}) \big] \approx \frac{1}{k} \sum_{i=1}^{k} \log (-v_{w_i}^{\prime \top} v_{w_I})
$$

So in practice, we have the optimization function

$$
\widehat{J} = \log \sigma(v_{w_O}^{\prime \top} v_{w_I}) + \sum_{i=1}^{k} \log (-v_{w_i}^{\prime \top} v_{w_I})
$$

Taking from my article “Noise Contrastive Estimation”, the optimization objective function for Noise Contrastive Estimation is

$$
J^{h}(\theta) = \mathbb{E}_{w \sim P_d^h(w)}\big[\log \sigma(\Delta s_{\theta^0}(w,h)) \big] + k \mathbb{E}_{w \sim P_n(w)}\big[\log (1 - \sigma(\Delta s_{\theta^0}(w,h))) \big]
$$

where $\Delta s_{\theta^0}(w,h) = s_{\theta^0}(w,h) - \log kP_n(w)$.

To estimate $J^{h}(\theta)$, we could use the following objective function.

$$
\begin{aligned}
{\widehat{J^{h}}}(\theta) &= \frac{1}{m} \sum_{i=1}^{m} \log \sigma(\Delta s_{\theta^0}(w_i,h)) + \frac{k}{n} \sum_{j=1}^{n} \log (1 - \sigma(\Delta s_{\theta^0}(w_j,h)))
\end{aligned}
$$

If we use $m=1$ and $n=k$, (but we do not have to),

$$
\begin{aligned}
{\widehat{J^{h}}}(\theta) &= \log \sigma(\Delta s_{\theta^0}(w,h)) + \sum_{j=1}^{k} \log (1 - \sigma(\Delta s_{\theta^0}(w_j,h)))
\end{aligned}
$$

We will rewrite it a little bit so that it looks close to the mathematical expression from the original papers.

$$
\begin{aligned}
{\widehat{J^{h}}}(\theta) &= \log \sigma(\Delta s_{\theta^0}(w,h)) + \sum_{j=1}^{k} \log (1 - \sigma(\Delta s_{\theta^0}(w_j,h))) \\
&= \log \sigma(\Delta s_{\theta^0}(w,h)) + \sum_{i=1}^{k} \log (1 - \sigma(\Delta s_{\theta^0}(w_i,h))) \\
&= \log \sigma(\Delta s_{\theta^0}(w,h)) + \sum_{i=1}^{k} \log \sigma(- \Delta s_{\theta^0}(w_i,h))
\end{aligned}
$$

where $w$ is the labeled word for the input, $w_i$ is the sampled words from the noise distribution, $\Delta s_{\theta^0}(w,h) = s_{\theta^0}(w,h) - \log kP_n(w)$.

Here if we use Noise Contrastive Estimation for the Word2Vec models we have just described.

$$
s_{\theta^0}(w,h) = v_{w}^{\prime \top} v_{w_I}
$$

We further have

$$
\begin{aligned}
{\widehat{J^{h}}}(\theta) &= \log \sigma(\Delta s_{\theta^0}(w,h)) + \sum_{i=1}^{k} \log \sigma(- \Delta s_{\theta^0}(w_i,h)) \\
&= \log \sigma(v_{w}^{\prime \top} v_{w_I} - \log kP_n(w)) + \sum_{i=1}^{k} \log \sigma(- v_{w}^{\prime \top} v_{w_I} + \log kP_n(w)) \\
\end{aligned}
$$

So we immediately found that Negative Sampling is nothing special but just setting $kP_n(w) = 1$ in Noise Contrastive Estimation!

The original authors said in the paper, “The main difference between the Negative sampling and NCE is that NCE needs both samples and the numerical probabilities of the noise distribution, while Negative sampling uses only samples. And while NCE approximately maximizes the log probability of the softmax, this property
is not important for our application.”

Since computing $kP_n(w)$ usually only takes $O(1)$ constant time, and as the authors admitted it no longer approximates maximum likelihood estimation, probably this Negative Sampling should not exist at all in my opinion.

In practice, people were using Noise Contrastive Estimation (NCE) loss to train Word2Vec models. This is also seen in the TensorFlow official Word2Vec tutorials.

But since Negative Sampling no longer does maximum likelihood estimation, how could it still successfully train the word embeddings in the first place in the original paper? I am going to show that the gradient of the optimization function is bounded such that it does not deviate from the gradient of the maximum likelihood estimation significantly. The sign of the gradient of the optimization function is also always the same as the sign of the gradient of the maximum likelihood estimation.

Still taking from my article “Noise Contrastive Estimation”, the gradient for the maximum likelihood estimation is

$$
\begin{aligned}
\frac{\partial}{\partial \theta} \mathbb{E}_{w \sim P_d^h(w)}\big[\log P_{\theta}^{h}(w)\big] &= \mathbb{E}_{w \sim P_d^h(w)}\big[ \frac{\partial}{\partial \theta} s_{\theta}(w,h) \big] - \mathbb{E}_{w \sim P_{\theta}^h(w)}\big[ \frac{\partial}{\partial \theta} s_{\theta}(w,h) \big] \\
&= \sum\limits_{w} P_{d}^{h}(w) \frac{\partial}{\partial \theta} s_{\theta}(w,h) - \sum\limits_{w} P_{\theta}^{h}(w) \frac{\partial}{\partial \theta} s_{\theta}(w,h) \\
&= \sum\limits_{w} \big( P_{d}^{h}(w) - P_{\theta}^{h}(w) \big) \frac{\partial}{\partial \theta} s_{\theta}(w,h) \\
&= \sum\limits_{w} \big( P_{d}^{h}(w) - P_{\theta}^{h}(w) \big) \frac{\partial}{\partial \theta} \log u_{\theta}(w,h)
\end{aligned}
$$

and the gradient for Noise Contrastive Estimation is

$$
\begin{aligned}
\frac{\partial}{\partial \theta} J^{h}(\theta) &= \mathbb{E}_{w \sim P_d^h(w)}\big[ \frac{kP_n(w)}{P_{\theta}^h(w) + kP_n(w)} \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \big] - k \mathbb{E}_{w \sim P_n(w)}\big[ \frac{P_{\theta}^h(w)}{P_{\theta}^h(w) + kP_n(w)} \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \big] \\
&= \sum \limits_{w} P_d^h(w) \frac{kP_n(w)}{P_{\theta}^h(w) + kP_n(w)} \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) - k\sum \limits_{w} P_n(w) \frac{P_{\theta}^h(w)}{P_{\theta}^h(w) + kP_n(w)} \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&= \sum \limits_{w} \frac{kP_n(w)}{P_{\theta}^h(w) + kP_n(w)} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
\end{aligned}
$$

Because in Negative Sampling, $kP_n(w) = 1$. The gradient for Negative Sampling is

$$
\begin{aligned}
\frac{\partial}{\partial \theta} J^{h}(\theta) &= \sum \limits_{w} \frac{kP_n(w)}{P_{\theta}^h(w) + kP_n(w)} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&= \sum \limits_{w} \frac{1}{P_{\theta}^h(w) + 1} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
\end{aligned}
$$

Because $0 \leq P_{\theta}^h(w) \leq 1$, and

$$
\frac{\partial}{\partial \theta} \mathbb{E}_{w \sim P_d^h(w)}\big[\log P_{\theta}^{h}(w)\big] = \sum\limits_{w} \big( P_{d}^{h}(w) - P_{\theta}^{h}(w) \big) \frac{\partial}{\partial \theta} \log u_{\theta}(w,h)
$$

we have

$$
\begin{aligned}
\frac{\partial}{\partial \theta} J^{h}(\theta) &= \sum \limits_{w} \frac{1}{P_{\theta}^h(w) + 1} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&\leq \sum \limits_{w} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&\leq \frac{\partial}{\partial \theta} \mathbb{E}_{w \sim P_d^h(w)}\big[\log P_{\theta}^{h}(w)\big]
\end{aligned}
$$

Similarly, we also have

$$
\begin{aligned}
\frac{\partial}{\partial \theta} J^{h}(\theta) &= \sum \limits_{w} \frac{1}{P_{\theta}^h(w) + 1} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&\geq \sum \limits_{w} \frac{1}{2} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&\geq \frac{1}{2} \sum \limits_{w} \big( P_d^h(w) - P_{\theta}^h(w) \big) \frac{\partial}{\partial \theta} \log P_{\theta}^h(w) \\
&\geq \frac{1}{2} \frac{\partial}{\partial \theta} \mathbb{E}_{w \sim P_d^h(w)}\big[\log P_{\theta}^{h}(w)\big]
\end{aligned}
$$

Therefore, we conclude that the gradient of the negative sampling is bounded by the gradient of maximum likelihood estimation, and the sign of the gradient of the negative sampling is also always the same as the sign of the gradient of maximum likelihood estimation.

$$
\frac{1}{2} \frac{\partial}{\partial \theta} \mathbb{E}_{w \sim P_d^h(w)}\big[\log P_{\theta}^{h}(w)\big] \leq \frac{\partial}{\partial \theta} J^{h}(\theta) \leq \frac{\partial}{\partial \theta} \mathbb{E}_{w \sim P_d^h(w)}\big[\log P_{\theta}^{h}(w)\big]
$$

Insights

If you are looking at the training of BERT which also learns the vector representations of tokens, the fundamental idea is very similar to the CBOW model. Essentially BERT is masking several words in a sentence and asked the model to predict the masked word during training. The Skip-Gram model has also influenced the Skip-Thought model to learn vector representation for sentences.

I may talk about these two models in depth in the future.

References

• Efficient Estimation of Word Representations in Vector Space
• Distributed Representations of Words and Phrases and their Compositionality

Appendix

Proof for the Equivalence of Different Skip-Gram Training Modes

The classification model is usually trained using maximum likelihood estimation. We use $q_{\theta}(x_i)$ to denote the predicted likelihood $q(x_i|\theta)$ from the model for sample $x_i$ from the dataset. Concretely, we have the following objective function

$$
\DeclareMathOperator*{\argmin}{argmin}
\DeclareMathOperator*{\argmax}{argmax}
\begin{aligned}
\argmax_{\theta} \prod_{i=1}^{n} q_{\theta}(y_i | x_i) &= \argmax_{\theta} \sum_{i=1}^{n} \log q_{\theta}(y_i | x_i) \\
&= \argmin_{\theta} - \sum_{i=1}^{n} \log q_{\theta}(y_i | x_i)
\end{aligned}
$$

$H_i(p,q_{\theta})$ is the cross entropy of sample $i$ in the dataset.

$$
\begin{aligned}
H_{i}(p,q_{\theta}) &= - \sum\limits_{y \in Y} p(y|x_i) \log q_{\theta}(y|x_i)
\end{aligned}
$$

If there is only one label $y_i$ for sample $i$,

$$
\begin{aligned}
H_{i}(p,q_{\theta}) &= - \sum\limits_{y \in Y} p(y|x_i) \log q_{\theta}(y|x_i) \\
&= - \log q_{\theta}(y_i|x_i) \\
\end{aligned}
$$

So in this case, we are minimizing the sum or average of the cross entropies from all the training examples.

$$
\begin{aligned}
\argmax_{\theta} \prod_{i=1}^{n} q_{\theta}(y_i | x_i) &= \argmin_{\theta} - \sum_{i=1}^{n} \log q_{\theta}(y_i | x_i) \\
&= \argmin_{\theta} \sum_{i=1}^{n} H_{i}(p,q_{\theta}) \\
&= \argmin_{\theta} \frac{1}{n} \sum_{i=1}^{n} H_{i}(p,q_{\theta}) \\
\end{aligned}
$$

Given a set of examples with the same input but different labels, $\\{(x_t, y_1),(x_t, y_2),\cdots,(x_t, y_m)\\}$, the average of the cross entropies from all the training examples would be

$$
\frac{1}{n} \sum_{i=1}^{n} H_{i}(p,q_{\theta}) = - \frac{1}{m} \sum_{i=1}^{m} \log q_{\theta}(y_i|x_t)
$$

If we convert the above $m$ examples to one single example with multiple labels with equal probability $\frac{1}{m}$, $\\{(x_t, (y_1, y_2,\cdots, y_m))\\}$, the cross entropy for this single example would be

$$
\begin{aligned}
H(p,q_{\theta}) &= - \sum\limits_{y \in Y} p(y|x_t) \log q_{\theta}(y|x_t) \\
&= - \sum_{i=1}^{m} p(y_i|x_t) \log q_{\theta}(y_i|x_t) \\
&= - \sum_{j=1}^{m} \frac{1}{m} \log q_{\theta}(y_i|x_t) \\
&= - \frac{1}{m} \sum_{j=1}^{m} \log q_{\theta}(y_i|x_t) \\
\end{aligned}
$$

This cross entropy is exactly the same as the average of the cross entropies from all the training examples from the previous case. Therefore, to train the Skip-Gram model, feeding a large batch consisting of $\{(x_t, y_1),(x_t, y_2),\cdots,(x_t, y_m)\}$ is equivalent to feeding a single example of $\{(x_t, (y_1, y_2,\cdots, y_m))\}$.