CUDA Shared Memory Swizzling

Introduction

When we write CUDA kernels that use shared memory, we have to be careful about shared memory bank conflicts. Having severe shared memory bank conflicts can introduce a significant performance penalty.

One simple way to deal with shared memory bank conflicts is to use padding. However, padding can waste shared memory and can have other drawbacks.

In this blog post, I would like to discuss how to deal with shared memory bank conflicts using swizzling. Swizzling is a more complicated technique that can be used to avoid shared memory bank conflicts without wasting shared memory.

CUDA Shared Memory Swizzling

Swizzling Example

When we use CUDA shared memory to cache data without using padding, it’s very common that either reading from or writing to shared memory by a warp can cause shared memory bank conflicts. Swizzling is a technique that rearranges the mapping of the shared memory index to avoid shared memory bank conflicts. Matrix transpose is a perfect example that can have shared memory bank conflicts if the implementation does not use padding or swizzling.

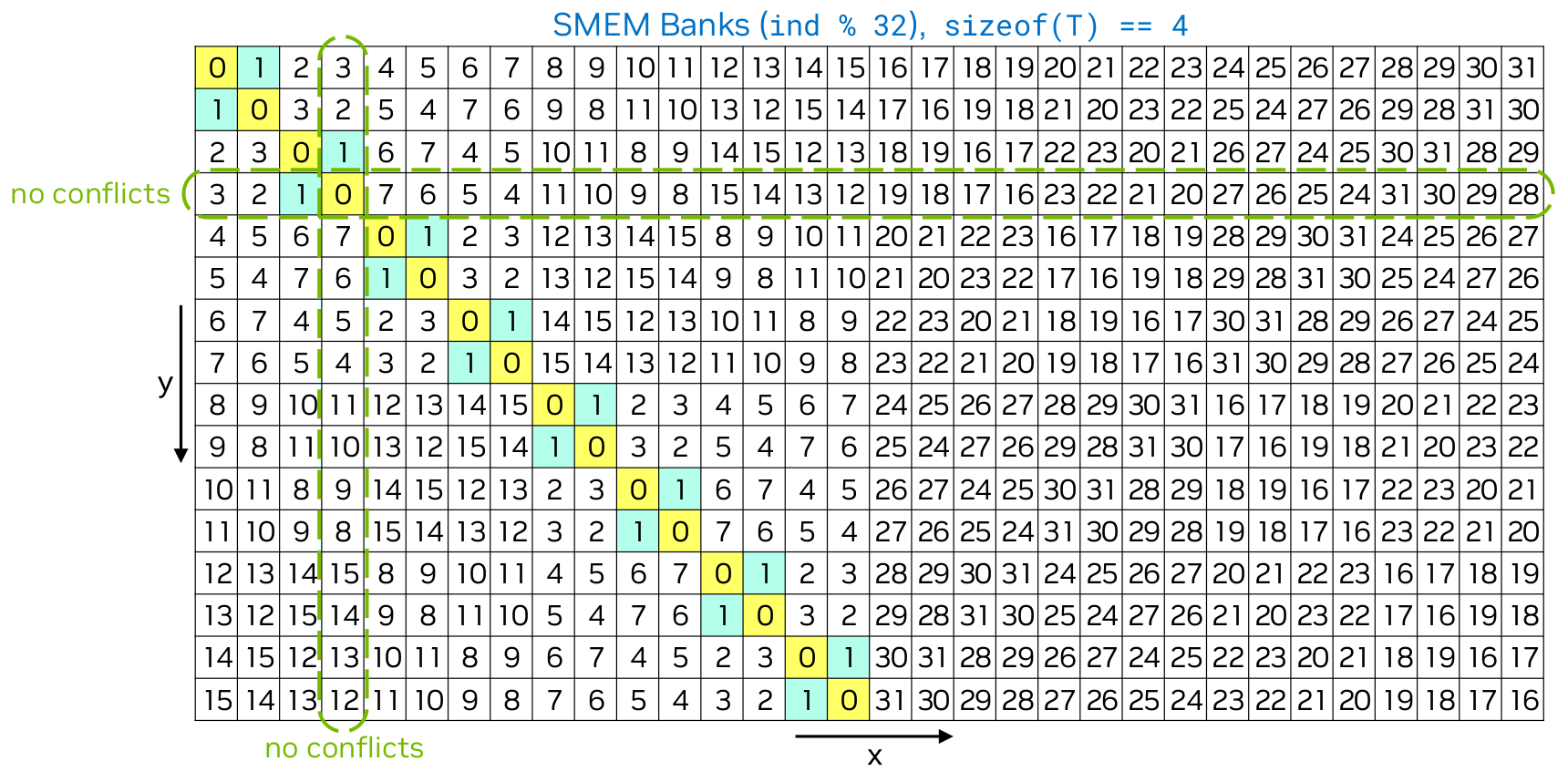
In the above example, the shared memory is a 2D array of float with size 32 × 16. In terms of matrix transpose, each warp reads a row of 32 values from the global memory and writes them to the shared memory with swizzling. There will be no shared memory bank conflicts when writing to the shared memory. To perform matrix transpose, each wrap reads two swizzled “columns” of 32 values from the shared memory and writes them to the global memory. For example, the swizzled column 0 and 1 are colored in yellow and cyan, respectively. In this way, there will be only one shared memory bank conflict when reading from the shared memory. Without using swizzling, there will be 16 (2-way) shared memory bank conflicts when reading from the shared memory. Of course, obviously, if the shared memory is a 2D array of float with size 32 × 32, there will be no shared memory bank conflicts when writing to the shared memory and reading from the shared memory.

Swizzling Formula

Given an array of T array[][NX] on shared memory, we define NX × sizeof(T) == SWIZZLE_SIZE. The allowed values of SWIZZLE_SIZE are powers of 2 that is larger than or equal to 32, such as 32, 64, 128, 256, …, etc.

Given the index [y][x] in T array[][NX], we can compute the swizzled index x_swz as follows:

1. Compute the index of the TC-byte chunk within SWIZZLE_SIZE-byte segment:
   i_chunk = (y × NX + x) × sizeof(T) / sizeof(TC)
y_chunk = i / (SWIZZLE_SIZE / sizeof(TC))
x_chunk = i % (SWIZZLE_SIZE / sizeof(TC))

2. Compute the swizzled index of TC-byte chunk using XOR operation:
   x_chunk_swz = y_chunk ^ x_chunk

3. Compute swizzled index:
   x_swz = x_chunk_swz × sizeof(TC) / sizeof(T) % NX + x % (sizeof(TC) / sizeof(T))

Swizzling Properties

This swizzling formula has the following properties:

1. The index before and after swizzling must be one to one mapped.
2. $\text{NX}$ must be a power of 2.
3. Given any $x$ and any $\{y, y+1, y+2, \cdots, y+31\}$, the number of unique swizzled index $x_{\text{swz}}$ should be maximized.

The property 1 ensures that there will be no data loss during swizzling. The property 2 ensures that the index before and after swizzling will be one to one mapped.

Here I am going to show some informal mathematical proofs for the properties from the swizzling formula.

Proof

We will first prove the property 1.

$$
\begin{align}
x_{\text{chunk}}
&= i_{\text{chunk}} \% (\text{SWIZZLE_SIZE} / \text{sizeof}(\text{TC})) \\
&= \left(\left(y × \text{NX} + x\right) × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})\right) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= \left(y × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) + x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})\right) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= \left(y × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) + x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \right) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= \left(x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \right) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= \left( x \% \text{NX} \right) × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \\
&= x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \\
\end{align}
$$

It seems that we have derived another equivalent formula for $x_{\text{chunk}}$. Note that $\text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})$ is a bit (right) shifting operation when $\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})$ is a power of 2.

$$
\begin{align}
y_{\text{chunk}}
&= i_{\text{chunk}} / (\text{SWIZZLE_SIZE} / \text{sizeof}(\text{TC})) \\
&= \left(\left(y × \text{NX} + x\right) × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})\right) / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= \left(y × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) + x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})\right) / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= y × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) + x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \\
&= y + x / \text{NX} \\
&= y \\
\end{align}
$$

It seems that we have also derived another equivalent formula for $y_{\text{chunk}}$.

$$
\begin{align}
x_{\text{chunk_swz}}
&= y_{\text{chunk}} \oplus x_{\text{chunk}} \\
&= y \oplus \left( x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \right) \\
&= y / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) + \left( y \% (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) \right) \oplus \left( x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \right) \\
&= y / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) + \left( \left( y \% \text{NX} \right) × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \right) \oplus \left( x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \right) \\
&= y / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) + \left( y \% \text{NX} \right) \oplus x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \\
\end{align}
$$

Note that $\oplus$ is the bitwise XOR operation. If either $y_{\text{chunk}}$ or $x_{\text{chunk}}$ is a constant, the mapping is a one to one mapping.

$$
\begin{align}
x_{\text{swz}}
&= x_{\text{chunk_swz}} × \text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}) \% \text{NX} + x \% (\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})) \\
\end{align}
$$

Here the proof becomes a little bit informal.

Because a consecutive of $\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})$ $x$ values will be mapped to one unique trunk index $x_{\text{chunk}}$, the mapping between $x_{\text{chunk}}$ and $x_{\text{chunk_swz}}$ is a one to one mapping, one $x_{\text{chunk_swz}}$ value will map to one unique $x_{\text{chunk_swz}} × \text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}) \% \text{NX}$ value. To create the one to one mapping between the swizzled index $x_{\text{swz}}$ and the original index $x$, the offset $x \% (\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}))$ is added. Therefore, the index before and after swizzling must be one to one mapped.

The property 2 is trivial to show.

The property 3 might be somewhat easier to see given the following expression for $x_{\text{swz}}$.

$$
\begin{align}
x_{\text{swz}}
&= x_{\text{chunk_swz}} × \text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}) \% \text{NX} + x \% (\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})) \\
&= \left( y / (\text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC})) × \text{NX} × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) + \left( y \% \text{NX} \right) \oplus x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) \right) × \text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}) \% \text{NX} + x \% (\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})) \\
&= \left( y \% \text{NX} \right) \oplus x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) × \text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}) \% \text{NX} + x \% (\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})) \\
&= \left( y \% \text{NX} \right) \oplus x × \text{sizeof}(\text{T}) / \text{sizeof}(\text{TC}) × \text{sizeof}(\text{TC}) / \text{sizeof}(\text{T}) + x \% (\text{sizeof}(\text{TC}) / \text{sizeof}(\text{T})) \\
\end{align}
$$

Given any $x$ and any $\{y, y+1, y+2, \cdots, y+\text{NX}-1\}$, the number of unique swizzled index $x_{\text{swz}}$ is $\text{NX}$ which is maximized.

Examples

Matrix Transpose

In this example, we implemented matrix transpose CUDA kernels using shared memory in three different ways:

1. Transpose with shared memory bank conflict.
2. Transpose without shared memory bank conflict via padding.
3. Transpose without shared memory bank conflict via swizzling.

transpose.cu

#include <algorithm>
#include <cassert>
#include <chrono>
#include <cstdio>
#include <functional>
#include <iomanip>
#include <iostream>
#include <random>
#include <vector>

#include <cuda_runtime.h>

#define CHECK_CUDA_ERROR(val) check((val), #val, __FILE__, __LINE__)
void check(cudaError_t err, char const* func, char const* file, int line)
{
    if (err != cudaSuccess)
    {
        std::cerr << "CUDA Runtime Error at: " << file << ":" << line
                  << std::endl;
        std::cerr << cudaGetErrorString(err) << " " << func << std::endl;
        std::exit(EXIT_FAILURE);
    }
}

#define CHECK_LAST_CUDA_ERROR() check_last(__FILE__, __LINE__)
void check_last(char const* file, int line)
{
    cudaError_t const err{cudaGetLastError()};
    if (err != cudaSuccess)
    {
        std::cerr << "CUDA Runtime Error at: " << file << ":" << line
                  << std::endl;
        std::cerr << cudaGetErrorString(err) << std::endl;
        std::exit(EXIT_FAILURE);
    }
}

template <class T>
float measure_performance(std::function<T(cudaStream_t)> bound_function,
                          cudaStream_t stream, size_t num_repeats = 10,
                          size_t num_warmups = 10)
{
    cudaEvent_t start, stop;
    float time;

    CHECK_CUDA_ERROR(cudaEventCreate(&start));
    CHECK_CUDA_ERROR(cudaEventCreate(&stop));

    for (size_t i{0}; i < num_warmups; ++i)
    {
        bound_function(stream);
    }

    CHECK_CUDA_ERROR(cudaStreamSynchronize(stream));

    CHECK_CUDA_ERROR(cudaEventRecord(start, stream));
    for (size_t i{0}; i < num_repeats; ++i)
    {
        bound_function(stream);
    }
    CHECK_CUDA_ERROR(cudaEventRecord(stop, stream));
    CHECK_CUDA_ERROR(cudaEventSynchronize(stop));
    CHECK_LAST_CUDA_ERROR();
    CHECK_CUDA_ERROR(cudaEventElapsedTime(&time, start, stop));
    CHECK_CUDA_ERROR(cudaEventDestroy(start));
    CHECK_CUDA_ERROR(cudaEventDestroy(stop));

    float const latency{time / num_repeats};

    return latency;
}

constexpr size_t div_up(size_t a, size_t b) { return (a + b - 1) / b; }

template <typename T, size_t BLOCK_TILE_SIZE_X = 32,
          size_t BLOCK_TILE_SIZE_Y = 32, size_t BLOCK_TILE_SKEW_SIZE_X = 0>
__global__ void transpose(T* output_matrix, T const* input_matrix, size_t M,
                          size_t N)
{
    // Waste some shared memory to avoid bank conflicts if
    // BLOCK_TILE_SKEW_SIZE_X != 0.
    __shared__ T
        shm[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X];

    // In some algorithms, such as matrix multiplication,
    // a warp of threads have to access a column of the 2D matrix in the shared
    // memory. Using the conventional index mapping, if the column size is not a
    // multiple of the warp size, there will be bank conflicts.
    size_t const input_matrix_from_idx_x{threadIdx.x + blockIdx.x * blockDim.x};
    size_t const input_matrix_from_idx_y{threadIdx.y + blockIdx.y * blockDim.y};
    size_t const input_matrix_from_idx{input_matrix_from_idx_x +
                                       input_matrix_from_idx_y * N};
    size_t const shm_to_idx_x{threadIdx.x};
    size_t const shm_to_idx_y{threadIdx.y};

    if ((input_matrix_from_idx_y < M) && (input_matrix_from_idx_x < N))
    {
        // Coalesced global memory access.
        // No shared memory bank conflict.
        shm[shm_to_idx_y][shm_to_idx_x] = input_matrix[input_matrix_from_idx];
    }

    // Make sure the buffer in a block is filled.
    __syncthreads();

    size_t const block_thread_idx{threadIdx.x + threadIdx.y * blockDim.x};
    size_t const shm_from_idx_x{block_thread_idx / BLOCK_TILE_SIZE_Y};
    size_t const shm_from_idx_y{block_thread_idx % BLOCK_TILE_SIZE_Y};
    size_t const output_matrix_to_idx_x{shm_from_idx_y +
                                        blockIdx.y * blockDim.y};
    size_t const output_matrix_to_idx_y{shm_from_idx_x +
                                        blockIdx.x * blockDim.x};
    size_t const output_matrix_to_idx{output_matrix_to_idx_x +
                                      output_matrix_to_idx_y * M};

    if ((output_matrix_to_idx_y < N) && (output_matrix_to_idx_x < M))
    {
        // Coalesced global memory access.
        // No shared memory bank conflict if BLOCK_TILE_SKEW_SIZE_X = 1.
        output_matrix[output_matrix_to_idx] =
            shm[shm_from_idx_y][shm_from_idx_x];
    }
}

template <typename T, size_t BLOCK_TILE_SIZE_X = 32,
          size_t BLOCK_TILE_SIZE_Y = 32>
__global__ void transpose_swizzling(T* output_matrix, T const* input_matrix,
                                    size_t M, size_t N)
{
    __shared__ T shm[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_X];

    // In some algorithms, such as matrix multiplication,
    // a warp of threads have to access a column of the 2D matrix in the shared
    // memory. Using the conventional index mapping, if the column size is not a
    // multiple of the warp size, there will be bank conflicts.
    size_t const input_matrix_from_idx_x{threadIdx.x + blockIdx.x * blockDim.x};
    size_t const input_matrix_from_idx_y{threadIdx.y + blockIdx.y * blockDim.y};
    size_t const input_matrix_from_idx{input_matrix_from_idx_x +
                                       input_matrix_from_idx_y * N};
    size_t const shm_to_idx_x{threadIdx.x};
    size_t const shm_to_idx_y{threadIdx.y};
    size_t const shm_to_idx_x_swizzled{(shm_to_idx_x ^ shm_to_idx_y) %
                                       BLOCK_TILE_SIZE_X};

    if ((input_matrix_from_idx_y < M) && (input_matrix_from_idx_x < N))
    {
        // Coalesced global memory access.
        // No shared memory bank conflict.
        shm[shm_to_idx_y][shm_to_idx_x_swizzled] =
            input_matrix[input_matrix_from_idx];
    }

    // Make sure the buffer in a block is filled.
    __syncthreads();

    size_t const block_thread_idx{threadIdx.x + threadIdx.y * blockDim.x};
    size_t const shm_from_idx_x{block_thread_idx / BLOCK_TILE_SIZE_Y};
    size_t const shm_from_idx_y{block_thread_idx % BLOCK_TILE_SIZE_Y};
    size_t const shm_from_idx_x_swizzled{(shm_from_idx_x ^ shm_from_idx_y) %
                                         BLOCK_TILE_SIZE_X};
    size_t const output_matrix_to_idx_x{shm_from_idx_y +
                                        blockIdx.y * blockDim.y};
    size_t const output_matrix_to_idx_y{shm_from_idx_x +
                                        blockIdx.x * blockDim.x};
    size_t const output_matrix_to_idx{output_matrix_to_idx_x +
                                      output_matrix_to_idx_y * M};

    if ((output_matrix_to_idx_y < N) && (output_matrix_to_idx_x < M))
    {
        // Coalesced global memory access.
        // No shared memory bank conflict.
        output_matrix[output_matrix_to_idx] =
            shm[shm_from_idx_y][shm_from_idx_x_swizzled];
    }
}

template <typename T>
void launch_transpose_with_shm_bank_conflict(T* d_output_matrix,
                                             T const* d_input_matrix, size_t M,
                                             size_t N, cudaStream_t stream)
{
    constexpr size_t BLOCK_TILE_SIZE_X{32};
    constexpr size_t BLOCK_TILE_SIZE_Y{32};
    constexpr size_t BLOCK_TILE_SKEW_SIZE_X{0};
    dim3 const block_size{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y};
    dim3 const grid_size{static_cast<unsigned int>(div_up(N, block_size.x)),
                         static_cast<unsigned int>(div_up(M, block_size.y))};
    transpose<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SKEW_SIZE_X>
        <<<grid_size, block_size, 0, stream>>>(d_output_matrix, d_input_matrix,
                                               M, N);
    CHECK_LAST_CUDA_ERROR();
}

template <typename T>
void launch_transpose_without_shm_bank_conflict_via_padding(
    T* d_output_matrix, T const* d_input_matrix, size_t M, size_t N,
    cudaStream_t stream)
{
    constexpr size_t BLOCK_TILE_SIZE_X{32};
    constexpr size_t BLOCK_TILE_SIZE_Y{32};
    constexpr size_t BLOCK_TILE_SKEW_SIZE_X{1};
    dim3 const block_size{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y};
    dim3 const grid_size{static_cast<unsigned int>(div_up(N, block_size.x)),
                         static_cast<unsigned int>(div_up(M, block_size.y))};
    transpose<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SKEW_SIZE_X>
        <<<grid_size, block_size, 0, stream>>>(d_output_matrix, d_input_matrix,
                                               M, N);
    CHECK_LAST_CUDA_ERROR();
}

template <typename T>
void launch_transpose_without_shm_bank_conflict_via_swizzling(
    T* d_output_matrix, T const* d_input_matrix, size_t M, size_t N,
    cudaStream_t stream)
{
    constexpr size_t BLOCK_TILE_SIZE_X{32};
    constexpr size_t BLOCK_TILE_SIZE_Y{32};
    dim3 const block_size{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y};
    dim3 const grid_size{static_cast<unsigned int>(div_up(N, block_size.x)),
                         static_cast<unsigned int>(div_up(M, block_size.y))};
    transpose_swizzling<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y><<<grid_size, block_size, 0, stream>>>(
        d_output_matrix, d_input_matrix, M, N);
    CHECK_LAST_CUDA_ERROR();
}

template <typename T>
bool is_equal(T const* data_1, T const* data_2, size_t size)
{
    for (size_t i{0}; i < size; ++i)
    {
        if (data_1[i] != data_2[i])
        {
            return false;
        }
    }
    return true;
}

template <typename T>
bool verify_transpose_implementation(
    std::function<void(T*, T const*, size_t, size_t, cudaStream_t)>
        transpose_function,
    size_t M, size_t N)
{
    // Fixed random seed for reproducibility
    std::mt19937 gen{0};
    cudaStream_t stream;
    size_t const matrix_size{M * N};
    std::vector<T> matrix(matrix_size, 0.0f);
    std::vector<T> matrix_transposed(matrix_size, 1.0f);
    std::vector<T> matrix_transposed_reference(matrix_size, 2.0f);
    std::uniform_real_distribution<T> uniform_dist(-256, 256);
    for (size_t i{0}; i < matrix_size; ++i)
    {
        matrix[i] = uniform_dist(gen);
    }
    // Create the reference transposed matrix using CPU.
    for (size_t i{0}; i < M; ++i)
    {
        for (size_t j{0}; j < N; ++j)
        {
            size_t const from_idx{i * N + j};
            size_t const to_idx{j * M + i};
            matrix_transposed_reference[to_idx] = matrix[from_idx];
        }
    }
    T* d_matrix;
    T* d_matrix_transposed;
    CHECK_CUDA_ERROR(cudaMalloc(&d_matrix, matrix_size * sizeof(T)));
    CHECK_CUDA_ERROR(cudaMalloc(&d_matrix_transposed, matrix_size * sizeof(T)));
    CHECK_CUDA_ERROR(cudaStreamCreate(&stream));
    CHECK_CUDA_ERROR(cudaMemcpy(d_matrix, matrix.data(),
                                matrix_size * sizeof(T),
                                cudaMemcpyHostToDevice));
    transpose_function(d_matrix_transposed, d_matrix, M, N, stream);
    CHECK_CUDA_ERROR(cudaStreamSynchronize(stream));
    CHECK_CUDA_ERROR(cudaMemcpy(matrix_transposed.data(), d_matrix_transposed,
                                matrix_size * sizeof(T),
                                cudaMemcpyDeviceToHost));
    bool const correctness{is_equal(matrix_transposed.data(),
                                    matrix_transposed_reference.data(),
                                    matrix_size)};
    CHECK_CUDA_ERROR(cudaFree(d_matrix));
    CHECK_CUDA_ERROR(cudaFree(d_matrix_transposed));
    CHECK_CUDA_ERROR(cudaStreamDestroy(stream));
    return correctness;
}

template <typename T>
float profile_transpose_implementation(
    std::function<void(T*, T const*, size_t, size_t, cudaStream_t)>
        transpose_function,
    size_t M, size_t N)
{
    constexpr int num_repeats{100};
    constexpr int num_warmups{10};
    cudaStream_t stream;
    size_t const matrix_size{M * N};
    T* d_matrix;
    T* d_matrix_transposed;
    CHECK_CUDA_ERROR(cudaMalloc(&d_matrix, matrix_size * sizeof(T)));
    CHECK_CUDA_ERROR(cudaMalloc(&d_matrix_transposed, matrix_size * sizeof(T)));
    CHECK_CUDA_ERROR(cudaStreamCreate(&stream));

    std::function<void(cudaStream_t)> const transpose_function_wrapped{
        std::bind(transpose_function, d_matrix_transposed, d_matrix, M, N,
                  std::placeholders::_1)};
    float const transpose_function_latency{measure_performance(
        transpose_function_wrapped, stream, num_repeats, num_warmups)};
    CHECK_CUDA_ERROR(cudaFree(d_matrix));
    CHECK_CUDA_ERROR(cudaFree(d_matrix_transposed));
    CHECK_CUDA_ERROR(cudaStreamDestroy(stream));

    return transpose_function_latency;
}

void print_latencty(std::string const& kernel_name, float latency)
{
    std::cout << kernel_name << ": " << std::fixed << std::setprecision(2)
              << latency << " ms" << std::endl;
}

int main()
{
    // Unit tests.
    for (size_t m{1}; m <= 64; ++m)
    {
        for (size_t n{1}; n <= 64; ++n)
        {
            assert(verify_transpose_implementation<float>(
                &launch_transpose_with_shm_bank_conflict<float>, m, n));
            assert(verify_transpose_implementation<float>(
                &launch_transpose_without_shm_bank_conflict_via_padding<float>,
                m, n));
            assert(verify_transpose_implementation<float>(
                &launch_transpose_without_shm_bank_conflict_via_swizzling<
                    float>,
                m, n));
        }
    }

    // M: Number of rows.
    size_t const M{8192};
    // N: Number of columns.
    size_t const N{8192};
    std::cout << M << " x " << N << " Matrix" << std::endl;
    float const latency_with_shm_bank_conflict{
        profile_transpose_implementation<float>(
            &launch_transpose_with_shm_bank_conflict<float>, M, N)};
    print_latencty("Transpose with Shared Memory Bank Conflict",
                   latency_with_shm_bank_conflict);
    float const latency_without_shm_bank_conflict_via_padding{
        profile_transpose_implementation<float>(
            &launch_transpose_without_shm_bank_conflict_via_padding<float>, M,
            N)};
    print_latencty("Transpose without Shared Memory Bank Conflict via Padding",
                   latency_without_shm_bank_conflict_via_padding);
    float const latency_without_shm_bank_conflict_via_swizzling{
        profile_transpose_implementation<float>(
            &launch_transpose_without_shm_bank_conflict_via_swizzling<float>, M,
            N)};
    print_latencty(
        "Transpose without Shared Memory Bank Conflict via Swizzling",
        latency_without_shm_bank_conflict_via_swizzling);

    return 0;
}

The program was built and performed on a platform that has an Intel i9-9900K CPU and an NVIDIA RTX 3090 GPU.

$ nvcc transpose.cu -o transpose
$ ./transpose
8192 x 8192 Matrix
Transpose with Shared Memory Bank Conflict: 1.10 ms
Transpose without Shared Memory Bank Conflict via Padding: 0.92 ms
Transpose without Shared Memory Bank Conflict via Swizzling: 0.92 ms

We could see that the transpose kernel with shared memory bank conflict has the highest latency, while the transpose kernel without shared memory bank conflict via padding and swizzling have the same latency and run 20% faster than the kernel with shared memory bank conflict in this case.

Note that this implementation achieves ~65% of the peak memory bandwidth of an RTX 3090 GPU. The performance can be further improved significantly using vectorized memory access if the implementation assumes the matrix is always padded (and usually allocated using cudaMallocPitch) so that each row will continue to meet the coalescing requirement.

Swizzling vs Padding

Swizzling and padding are two common techniques to deal with shared memory bank conflicts.

The advantage of swizzling is that it does not waste shared memory space. The disadvantage of swizzling is that it is more complicated to implement and understand because the index mapping is not linear.

The advantage of padding is that it is simple to implement and understand. The disadvantage of padding is that it wastes shared memory space and can break the address alignment of the data if the padding size is not selected carefully especially when we access the data via large trunks using reinterpret_cast and cause undefined behaviors. This usually happens when vectorized memory access is performed on 2D padded arrays which accidentally breaks the alignment of the data.

References

• CUDA Coalesced Memory Access
• CUDA Shared Memory Bank
• Swizzling - Wikipedia
• Advanced Performance Optimization in CUDA - NVIDIA GTC 2024
• Using TMA to Transfer Multi-Dimensional Arrays - CUDA Programming Guide
• CUtensorMapSwizzle - CUDA Driver API