Deformable Attention
Introduction
Transformer multi-head attention is a mechanism that allows a neural network to focus on a small set of features from a large set of features. However, the vanilla multi-head attention mechanism is usually very expensive to compute and slows down training convergence, especially for computer vision models. Deformable multi-head attention was developed to reduce the computational complexity of the attention mechanism for computer vision models.
In this blog post, I would like to discuss the vanilla multi-head attention, the deformable multi-head attention, and the deformable multi-head attention v2 in detail.
Multi-Head Attention
Multi-Head Attention Formulation
Let $q \in \Omega_q$ indexes a query element with representation feature $\mathbf{z}_q \in \mathbb{R}^{C \times 1}$, and $k \in \Omega_k$ indexes a key element with representation feature $\mathbf{x}_k \in \mathbb{R}^{C \times 1}$, where $C$ is the feature dimension, and $\Omega_q$ and $\Omega_k$ are the query and key element sets, respectively. The multi-head attention feature is computed as follows:
$$
\begin{aligned}
\text{MultiHeadAttention}(\mathbf{z}_q, \mathbf{X}) &= \sum_{m = 1}^{M} \mathbf{W}_m \left[ \sum_{k \in \Omega_k}^{} A_{m,q,k} \mathbf{W}_m^{\prime} \mathbf{x}_{k} \right] \\
\end{aligned}
$$
where $m$ indexes the attention head, $M$ is the number of attention heads, $\mathbf{W}_m \in \mathbb{R}^{C \times C_{v}}$ and $\mathbf{W}_m^{\prime} \in \mathbb{R}^{C_{v} \times C}$ are the learnable weight matrices for the $m$-th attention head, $C_{v} = \frac{C}{M}$ by default, and $A_{m,q,k} \in \mathbb{R}$ is the attention weight between the query element $q$ and the key element $k$ for the $m$-th attention head.
The attention weight $A_{m,q,k}$, which is normalized, is computed as follows using a softmax function:
$$
\begin{aligned}
A_{m,q,k} &= \frac{\exp \left( \text{score}(\mathbf{z}_q, \mathbf{x}_k) \right)}{\sum_{k^{\prime} \in \Omega_k}^{} \exp \left( \text{score}(\mathbf{z}_q, \mathbf{x}_{k^{\prime}}) \right)} \\
&= \frac{\exp \left( \frac{\left( \mathbf{U}_m \mathbf{z}_q \right)^{\top} \mathbf{V}_m \mathbf{x}_k}{\sqrt{C_v}} \right)}{\sum_{k^{\prime} \in \Omega_k}^{} \exp \left( \frac{\left( \mathbf{U}_m \mathbf{z}_q \right)^{\top} \mathbf{V}_m \mathbf{x}_{k^{\prime}}}{\sqrt{C_v}} \right)} \\
&= \frac{\exp \left( \frac{ \mathbf{z}_q^{\top} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{x}_k }{\sqrt{C_v}} \right)}{\sum_{k^{\prime} \in \Omega_k}^{} \exp \left( \frac{\mathbf{z}_q^{\top} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{x}_{k^{\prime}}}{\sqrt{C_v}} \right)} \\
\end{aligned}
$$
where $\mathbf{U}_m \in \mathbb{R}^{C_{v} \times C}$ and $\mathbf{V}_m \in \mathbb{R}^{C_{v} \times C}$ are the learnable weight matrices for the $m$-th attention head, and $\text{score}(\mathbf{z}_q, \mathbf{x}_k) = \frac{ \mathbf{z}_q^{\top} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{x}_k }{\sqrt{C_v}}$ is the attention score between the query element $q$ and the key element $k$ for the $m$-th attention head.
$\sum_{k \in \Omega_k}^{} A_{m,q,k} \mathbf{W}_m^{\prime} \mathbf{x}_{k}$ for all the queries can be computed using vectorization as follows:
$$
\begin{aligned}
\mathbf{A}_{m} \mathbf{X} \mathbf{W}_m^{\prime \top}
&= \text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \left(\mathbf{X} \mathbf{V}_m^{\top} \right)^{\top}}{\sqrt{C_v}} \right) \mathbf{X} \mathbf{W}_m^{\prime \top} \\
&= \text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{X}^{\top}}{\sqrt{C_v}} \right) \mathbf{X} \mathbf{W}_m^{\prime \top} \\
\end{aligned}
$$
where $\mathbf{Z} \in \mathbb{R}^{N_q \times C}$ and $\mathbf{X} \in \mathbb{R}^{N_k \times C}$ are the query feature matrix and the key feature matrix, respectively, and $\mathbf{A}_{m} \in \mathbb{R}^{N_q \times N_k}$ is the attention weight matrix for the $m$-th attention head.
The multi-head attention feature for all the queries is computed as follows:
$$
\begin{aligned}
\text{MultiHeadAttention}(\mathbf{Z}, \mathbf{X})
&= \sum_{m = 1}^{M} \mathbf{A}_{m} \mathbf{X} \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
&= \sum_{m = 1}^{M} \text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{X}^{\top}}{\sqrt{C_v}} \right) \mathbf{X} \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
\end{aligned}
$$
Multi-Head Attention Computational Complexity
Suppose each multiply-accumulate (MAC) operation takes $O(1)$ time, let’s compute the computational complexity of the multi-head attention for $N_q$ queries and $N_k$ keys.
The computational complexity of the multi-head attention for $N_q$ queries and $N_k$ keys can be derived as follows:
$$
\begin{aligned}
O\left( M \left( \underbrace{O( N_k C C_{v} ) + O( N_k C_{v} C )}_{\mathbf{X} \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top}} + \underbrace{O( N_k C C_{v} ) + O( N_q C C_{v} ) + O(N_q N_k C_v) + O(N_q N_k)}_{\text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{X}^{\top}}{\sqrt{C_v}} \right)} + O(N_q N_k C_v) \right) \right)
&= O\left( M \left( O( N_k C C_{v} ) + O( N_q C C_{v} ) + O( N_q N_k C_v ) \right) \right) \\
&= O( N_k C^2 ) + O( N_q C^2 ) + O( N_q N_k C ) \\
&= O( N_k C^2 + N_q C^2 + N_q N_k C ) \\
\end{aligned}
$$
In modern Transformer based large language models, for both encoder and decoder, $N_q$ and $N_k$ can be very large and much larger than $C$, therefore, the computational complexity of the multi-head attention is dominated by the third term, $O( N_q N_k C )$.
In Transformer based computer vision models, the values of $N_q$, $N_k$, and $C$ can be quite different in the encoder and decoder, therefore affecting the asymptotic computational complexity of the multi-head attention.
For the encoder, because all the attention layers are self-attention, $N_q = N_k = HW$ where $H$ and $W$ are the height and width of the feature map, respectively. Because usually $HW \gg C$, the computational complexity of the multi-head attention is $O( N_q N_k C ) = O( H^2 W^2 C )$.
For the decoder, the number of queries $N_q$ is much smaller than the one in the encoder. In the self-attention layers, $N_q = N_k = N$, which might be comparable to $C$, the computational complexity of the multi-head attention is $O( NC^2 + N^2 C )$. In the cross-attention layers, $N_q = N$ and $N_k = HW$. Because usually $HW \gg C$ and $HW \gg N$, the computational complexity of the multi-head attention is $O( HWC^2 + NHWC )$.
It’s not hard to see that the computational complexity of the multi-head attention in the encoder self-attention layers and the decoder cross-attention layers are quite expensive. Deformable attention was devised to reduce the computational complexity of the multi-head attention in these layers for computer vision models.
Deformable Multi-Head Attention
Deformable Multi-Head Attention Formulation
Inspired by the deformable convolution, the deformable multi-head attention only attends to a small set of the keys sampled around a reference point in the spatial dimension for each query for computer vision models.
Given an input feature map $\mathbf{X} \in \mathbb{R}^{C \times H \times W}$, let $q \in \Omega_q$ indexes a query element with representation feature $\mathbf{z}_q \in \mathbb{R}^{C}$, and $\mathbf{p}_q$ denotes the reference point for $q$, the deformable multi-head attention feature is computed as follows:
$$
\begin{aligned}
\text{DeformableMultiHeadAttention}(\mathbf{z}_q, \mathbf{p}_q, \mathbf{X}) &= \sum_{m = 1}^{M} \mathbf{W}_m \left[ \sum_{k = 1}^{K} A_{m,q,k} \mathbf{W}_m^{\prime} \mathbf{x}(\mathbf{p}_q + \Delta\mathbf{p}_{m,q,k}) \right] \\
\end{aligned}
$$
where $m$ indexes the attention head, $M$ is the number of attention heads, $\mathbf{W}_m \in \mathbb{R}^{C \times C_{v}}$ and $\mathbf{W}_m^{\prime} \in \mathbb{R}^{C_{v} \times C}$ are the learnable weight matrices for the $m$-th attention head, $C_{v} = \frac{C}{M}$ by default, $k$ indexes the sampled key element, $K$ is the number of sampled key elements, $\Delta\mathbf{p}_{m,q,k}$ is the offset for the sampled key element $k$ for the $m$-th attention head, and $A_{m,q,k} \in \mathbb{R}$ is the attention weight between the query element $q$ and the sampled key element $k$ for the $m$-th attention head.
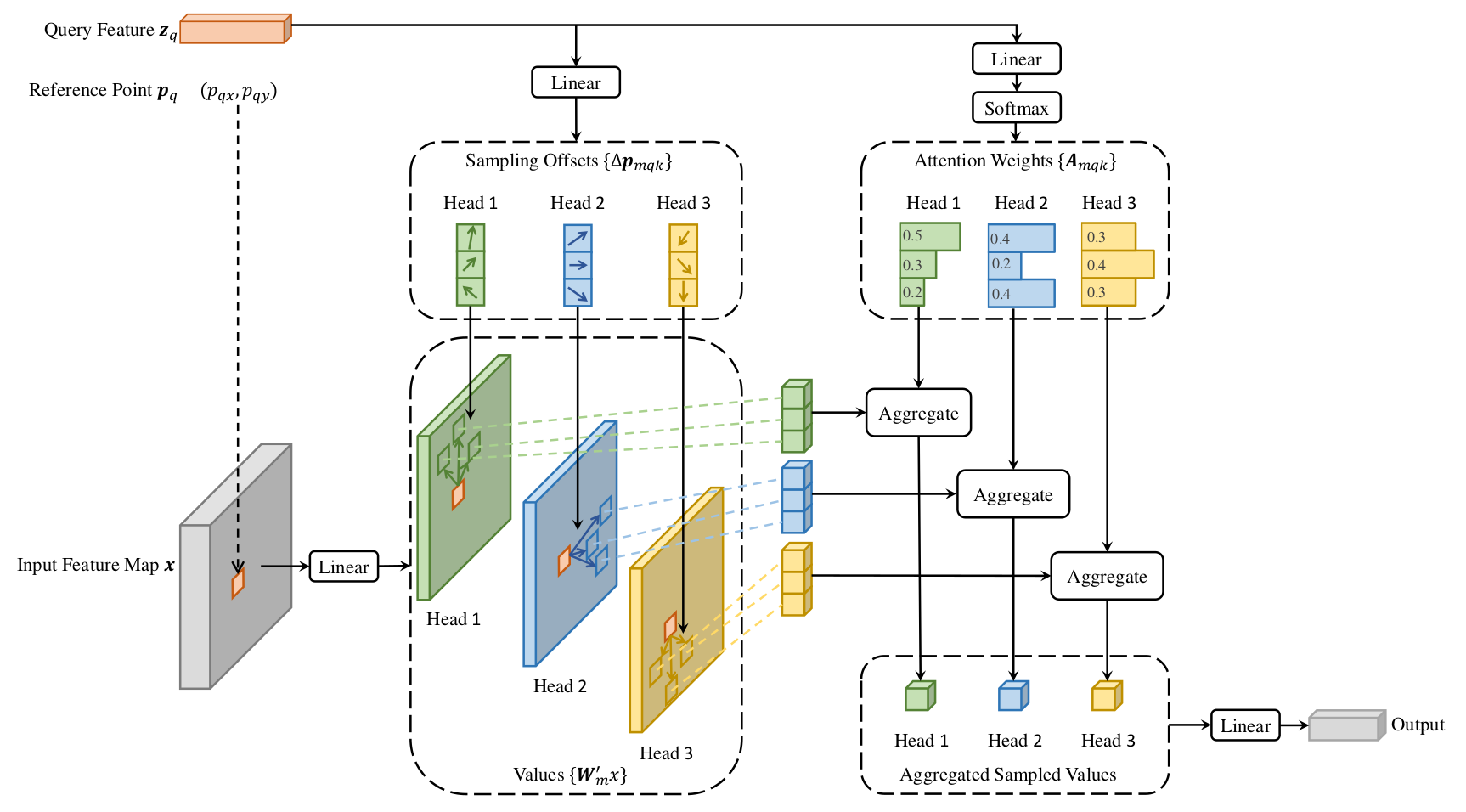
To effectively reduce the computational complexity of the multi-head attention, the number of sampled key elements $K$ should be much smaller than the number of all the key elements $N_k$, i.e., $K \ll N_k$. Similar to the deformable convolution, $\mathbf{x}(\mathbf{p}_q + \Delta\mathbf{p}_{m,q,k})$ can be interpolated from the neighboring pixels on the input feature map.
Although the offset $\Delta\mathbf{p}_{m,q,k}$ is also learned, just like the one in the deformable convolution, it is usually learned by a linear layer instead of a convolution. This might seem to be inferior because the offset prediction now only depends on the query element $q$ for each attention head $m$, and its neighbor pixels will not be considered.
$$
\begin{aligned}
\Delta\mathbf{p}_{m,q,k} &= \mathbf{W}^{\prime\prime}_{m,k} \mathbf{z}_q \\
\end{aligned}
$$
where $\mathbf{W}^{\prime\prime}_{m,k} \in \mathbb{R}^{2 \times C}$ is the learnable weight matrix for the $k$-th sampled key element for the $m$-th attention head.
The attention weight $A_{m,q,k}$ is computed quite differently from the one in the multi-head attention. Instead of computing the attention score between the query element $q$ and the key element $k$ via dot product, the attention weight only depends on the query element $q$ for each attention head $m$. The attention weight $A_{m,q,k}$ is computed as follows using a softmax function:
$$
\begin{aligned}
A_{m,q,k} &= \frac{\exp \left( \mathbf{W}^{\prime\prime\prime}_{m,k} \mathbf{z}_q \right)}{\sum_{k^{\prime} = 1}^{K} \exp \left( \mathbf{W}^{\prime\prime\prime}_{m,k^{\prime}} \mathbf{z}_q \right)} \\
\end{aligned}
$$
where $\mathbf{W}^{\prime\prime\prime}_{m,k} \in \mathbb{R}^{1 \times C}$ is the learnable weight vector for the $k$-th sampled key element for the $m$-th attention head.
The deformable multi-head attention feature for all the queries is computed as follows:
$$
\begin{aligned}
\text{DeformableMultiHeadAttention}(\mathbf{Z}, \mathbf{P}, \mathbf{X})
&= \sum_{m = 1}^{M} \mathbf{A}_{m} \mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \right) \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
&= \sum_{m = 1}^{M} \text{softmax}\left( \mathbf{Z} \mathbf{W}^{\prime\prime\prime\top}_m \right) \mathbf{X}\left( \mathbf{P} + \mathbf{Z} \mathbf{W}^{\prime\prime\top}_{m}
\right) \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
\end{aligned}
$$
where $\mathbf{Z} \in \mathbb{R}^{N_q \times C}$ and $\mathbf{P} \in \mathbb{R}^{N_q \times 2}$ are the query feature matrix and the reference point matrix, respectively, $\Delta\mathbf{P}_m \in \mathbb{R}^{N_q \times K \times 2}$ is the offset matrix for the $m$-th attention head, and $\mathbf{A}_{m} \in \mathbb{R}^{N_q \times K}$ is the attention weight matrix for the $m$-th attention head, and $\mathbf{W}^{\prime\prime}_{m} \in \mathbb{R}^{K \times 2 \times C}$ and $\mathbf{W}^{\prime\prime\prime}_{m} \in \mathbb{R}^{K \times C}$ are the learnable weight matrices for the $m$-th attention head. $\mathbf{Z} \mathbf{W}^{\prime\prime\prime\top}_m \in \mathbb{R}^{N_q \times K}$ is the attention score matrix for the $m$-th attention head, $\mathbf{X}\left( \mathbf{P} + \mathbf{Z} \mathbf{W}^{\prime\prime\top}_{m}
\right) \in \mathbb{R}^{N_q \times K \times C}$ is the sampled key feature matrix for the $m$-th attention head, $\text{softmax}\left( \mathbf{Z} \mathbf{W}^{\prime\prime\prime\top}_m \right) \mathbf{X}\left( \mathbf{P} + \mathbf{Z} \mathbf{W}^{\prime\prime\top}_{m}
\right) \in \mathbb{R}^{N_q \times C}$.
Deformable Multi-Head Attention Computational Complexity
The computational complexity of the multi-head attention for $N_q$ queries and $K$ sampled keys per query can be derived as follows:
$$
\begin{aligned}
O\left( M \left( \underbrace{O\left(\min\left( N_q KC + N_q KC + N_q KC_v C , N_q KC + N_k C_v C + N_q K C_v \right)\right)}_{\mathbf{X}\left( \mathbf{P} + \mathbf{Z} \mathbf{W}^{\prime\prime\top}_{m}
\right) \mathbf{W}_m^{\prime \top} } + \underbrace{O\left(N_q K C + N_q K\right)}_{\text{softmax}\left( \mathbf{Z} \mathbf{W}^{\prime\prime\prime\top}_m \right)} + O(N_q K C_v) + O(N_q C C_v) \right) \right)
&= O\left( N_q K C M + N_q K C + N_q C^2 + \min\left( N_q K C^2, N_k C^2 \right)\right) \\
&= O\left( N_q C^2 + \min\left( N_q K C^2, N_k C^2 \right)\right) \\
\end{aligned}
$$
where $N_k$ is the number of all the key elements and $N_k = HW$. We have a $\min$ operation in the first term because we could either do feature sampling followed by feature transformation or feature transformation followed by feature sampling, whichever is cheaper depending on the values of $N_q$, $N_k = HW$, and $K$.
For the Transformer based computer vision model encoder, because all the attention layers are self-attention, $N_q = N_k = HW$ where $H$ and $W$ are the height and width of the feature map, respectively. The computational complexity of the deformable multi-head attention is $O( N_q C^2 ) = O( H W C^2 )$. Comparing to the $O( H^2 W^2 C )$ computational complexity of the multi-head attention, the computational complexity of the deformable multi-head attention is much cheaper in most cases.
For the decoder, the computational complexity of the deformable multi-head attention is $O( NKC^2 )$ for both the self-attention layers and the cross-attention layers. Comparing to the $O( NC^2 + N^2 C )$ computational complexity of the multi-head attention in the self-attention layers, the computational complexity of the deformable multi-head attention is comparable. Comparing to the $O( HWC^2 + NHWC )$ computational complexity of the multi-head attention in the cross-attention layers, the computational complexity of the deformable multi-head attention is much cheaper in almost all cases.
Deformable Multi-Head Attention VS Deformable Convolution
The deformable multi-head attention degenerates to $R \times S$ deformable convolution, where $R$ is the convolution kernel height and $S$ is the convolution kernel width, when $M = RS$, $K = 1$, and $\mathbf{W}_m^{\prime} = \mathbf{I}$ which is an identity matrix.
Multi-Scale Deformable Multi-Head Attention
Multi-Scale Deformable Multi-Head Attention Formulation
The deformable multi-head attention can be naturally extended to multi-scale deformable multi-head attention to support the multi-scale feature maps from the neural network modules such as feature pyramid network (FPN). It allows the attention to be computed on multiple feature maps with different spatial resolutions.

Given $L$ feature maps $\{\mathbf{X}\}_{l=1}^{L}$ with different spatial resolutions. The $l$-th feature map ${\mathbf{X}}_{l}$ has spatial dimension $H^{l} \times W^{l}$. let $q \in \Omega_q$ indexes a query element with representation feature $\mathbf{z}_q \in \mathbb{R}^{C}$, and $\hat{\mathbf{p}}_q \in [0, 1]^2$ denotes the normalized reference point for $q$, the multi-scale deformable multi-head attention feature is computed as follows:
$$
\begin{aligned}
\text{MultiScaleDeformableMultiHeadAttention}(\mathbf{z}_q, \hat{\mathbf{p}}_q, \{\mathbf{X}\}_{l=1}^{L})
&= \sum_{m = 1}^{M} \mathbf{W}_m \left[ \sum_{l = 1}^{L} \sum_{k = 1}^{K} A_{m,q,l,k} \mathbf{W}_m^{\prime} \mathbf{x}_{l}(\hat{\mathbf{p}}_q + \Delta\mathbf{p}_{m,q,l,k}) \right] \\
\end{aligned}
$$
where $m$ indexes the attention head, $M$ is the number of attention heads, $\mathbf{W}_m \in \mathbb{R}^{C \times C_{v}}$ and $\mathbf{W}_m^{\prime} \in \mathbb{R}^{C_{v} \times C}$ are the learnable weight matrices for the $m$-th attention head, $C_{v} = \frac{C}{M}$ by default, $l$ indexes the feature map, $L$ is the number of feature maps, $k$ indexes the sampled key element, $K$ is the number of sampled key elements, $\Delta\mathbf{p}_{m,q,l,k}$ is the offset for the sampled key element $k$ for the $m$-th attention head, and $A_{m,q,l,k} \in \mathbb{R}$ is the attention weight between the query element $q$ and the sampled key element $k$ for the $m$-th attention head and $\sum_{l = 1}^{L} \sum_{k = 1}^{K} A_{m,q,l,k} = 1$.
Deformable Multi-Head Attention V2
Deformable Multi-Head Attention Drawbacks
Taking a closer look at the deformable multi-head attention mentioned previously, we can see that the attention weight $A_{m,q,k}$ is computed quite differently from the one in the vanilla multi-head attention. Instead of computing the attention score between the query element $q$ and the key element $k$ via dot product, the attention weight only depends on the query element $q$ for each attention head $m$, which is something a little bit strange in the context of Transformer attention. In fact, the deformable multi-head attention is more closer to convolution than attention.
The deformable multi-head attention also has a drawback of higher memory consumption than the vanilla multi-head attention, especially for the self-attention in the Transformer encoders. In the vanilla multi-head attention, the largest memory consumption comes from the feature map tensor $\mathbf{X} \in \mathbb{R}^{H \times W \times C}$, which is usually very large. In the deformable multi-head attention, because of the new sampled key elements, the memory consumption would be the intermediate sampled key tensor $\mathbf{X} \in \mathbb{R}^{N_q \times K \times C}$. In the Transformer encoders for computer vision models, $N_q = N_k = HW$ is already very large, having $N_q K C = HWKC$ is even more expensive than the vanilla multi-head attention.
When the deformable multi-head attention was first proposed for Transformer based computer vision models, the Vision Transformer (ViT) has not been developed yet. Therefore, the deformable multi-head attention was only used in the task head and the feature extraction backbone was still a convolutional neural network (CNN) for Deformable-DETR, producing a feature map of reasonable sized $H$ and $W$, so that the deformable multi-head attention would not be too expensive. In addition, because the deformable multi-head attention was only used in the task head, using small $K$ would not affect the performance too much while reducing the memory consumptions.
The ViT uses the multi-head attention in the Transformer encoders for feature extraction. In this case, because $H$ and $W$ become much larger, the deformable multi-head attention would be too expensive to use. In addition, using small $K$ would affect feature exaction from the backbone. Therefore, using the deformable multi-head attention mentioned above in the Transformer encoders for feature extraction is not a good idea. A new deformable multi-head attention v2 was developed to address these issues more specifically for the ViT.
Deformable Multi-Head Attention V2 Formulation
Developed based on the deformable multi-head attention, the key idea of the deformable multi-head attention v2 is to use a set of global shifted keys shared among all the queries for each attention head. This design is more naturally extended from the vanilla multi-head attention, and it also reduces the memory consumption.
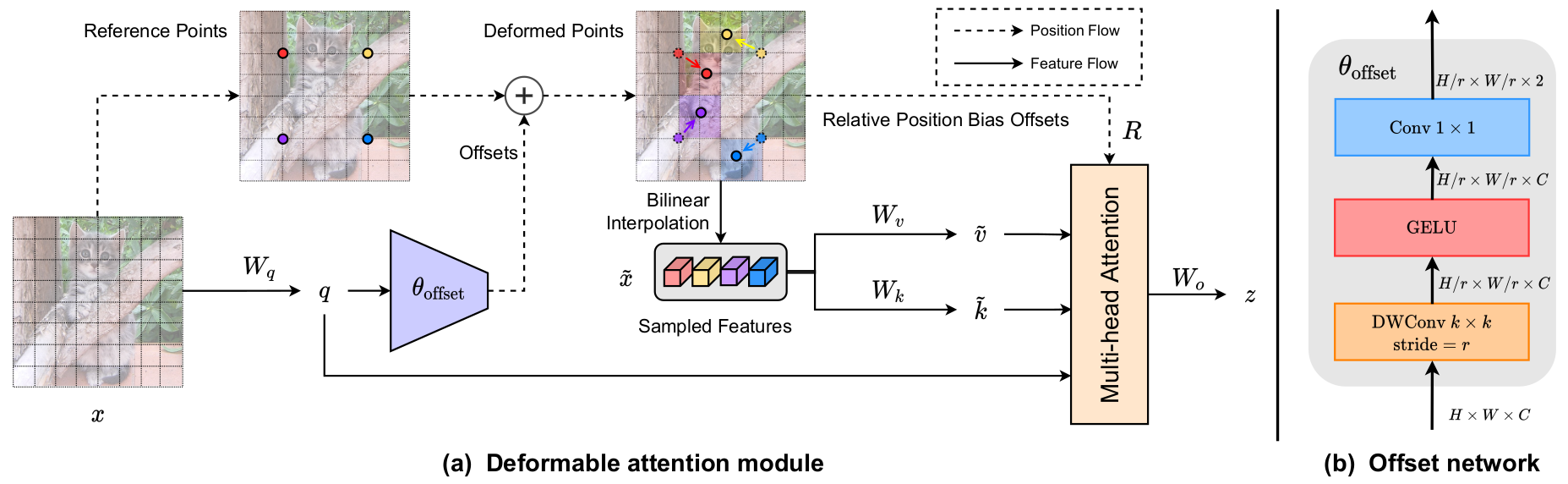
In the deformable multi-head attention v2, given an input feature map $\mathbf{X} \in \mathbb{R}^{C \times H \times W}$, let $q \in \Omega_q$ indexes a query element with representation feature $\mathbf{z}_q \in \mathbb{R}^{C}$, and $\mathbf{p}_q$ denotes the reference point for $q$, the deformable multi-head attention v2 feature is computed as follows:
$$
\begin{aligned}
\text{DeformableMultiHeadAttentionV2}(\mathbf{z}_q, \mathbf{p}_q, \mathbf{X}) &= \sum_{m = 1}^{M} \mathbf{W}_m \left[ \sum_{k = 1}^{K} A_{m,q,k} \mathbf{W}_m^{\prime} \mathbf{x}(\mathbf{p}_q + \Delta\mathbf{p}_{m,k}) \right] \\
\end{aligned}
$$
where $m$ indexes the attention head, $M$ is the number of attention heads, $\mathbf{W}_m \in \mathbb{R}^{C \times C_{v}}$ and $\mathbf{W}_m^{\prime} \in \mathbb{R}^{C_{v} \times C}$ are the learnable weight matrices for the $m$-th attention head, $C_{v} = \frac{C}{M}$ by default, $k$ indexes the sampled key element, $K$ is the number of sampled key elements, $\Delta\mathbf{p}_{m,k}$ is the offset for the sampled key element $k$ for the $m$-th attention head, and $A_{m,q,k} \in \mathbb{R}$ is the attention weight between the query element $q$ and the sampled key element $k$ for the $m$-th attention head. Notice that unlike the offset $\Delta\mathbf{p}_{m,q,k}$ used in the deformable multi-head attention that is learned for each query element $q$, the offset $\Delta\mathbf{p}_{m,k}$ used in the deformable multi-head attention v2 is shared among all the query elements.
The attention weight $A_{m,q,k}$, which is normalized, is computed almost the same as the one in the vanilla deformable multi-head attention:
$$
\begin{aligned}
A_{m,q,k} &= \frac{\exp \left( \text{score}(\mathbf{z}_q, \mathbf{x}_k) + b_{m, k} \right)}{\sum_{k^{\prime} = 1}^{K} \exp \left( \text{score}(\mathbf{z}_q, \mathbf{x}_{k^{\prime}}) + b_{m, k} \right)} \\
&= \frac{\exp \left( \frac{\left( \mathbf{U}_m \mathbf{z}_q \right)^{\top} \mathbf{V}_m \mathbf{x}_k}{\sqrt{C_v}} + b_{m, k} \right)}{\sum_{k^{\prime} = 1}^{K} \exp \left( \frac{\left( \mathbf{U}_m \mathbf{z}_q \right)^{\top} \mathbf{V}_m \mathbf{x}_{k^{\prime}}}{\sqrt{C_v}} + b_{m, k} \right)} \\
&= \frac{\exp \left( \frac{ \mathbf{z}_q^{\top} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{x}_k }{\sqrt{C_v}} + b_{m, k} \right)}{\sum_{k^{\prime} = 1}^{K} \exp \left( \frac{\mathbf{z}_q^{\top} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{x}_{k^{\prime}}}{\sqrt{C_v}} + b_{m, k} \right)} \\
\end{aligned}
$$
where $\mathbf{U}_m \in \mathbb{R}^{C_{v} \times C}$ and $\mathbf{V}_m \in \mathbb{R}^{C_{v} \times C}$ are the learnable weight matrices for the $m$-th attention head, and $\text{score}(\mathbf{z}_q, \mathbf{x}_k) = \frac{ \mathbf{z}_q^{\top} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{x}_k }{\sqrt{C_v}}$ is the attention score between the query element $q$ and the key element $k$ for the $m$-th attention head, and $b_{m, k} \in \mathbb{R}$ is the bias for the $k$-th sampled key element for the $m$-th attention head originally developed for the Swin Transformer. The bias $b_{m, k}$ is interpolated from a bias table and its computational cost is negligible comparing to the dominating attention score computation.
The offset $\Delta\mathbf{p}_{m,k}$ depends on all the query elements $q$ for each attention head $m$, and it is computed as follows:
$$
\begin{aligned}
\Delta\mathbf{p}_{m,k} &= f_{m,k} (\mathbf{Z}) \\
\end{aligned}
$$
where $f_{m,k} (\mathbf{Z})$ is a function of the query feature matrix $\mathbf{Z} \in \mathbb{R}^{N_q \times C}$ for the $m$-th attention head.
The deformable multi-head attention v2 feature for all the queries is computed as follows:
$$
\begin{aligned}
\text{DeformableMultiHeadAttentionV2}(\mathbf{Z}, \mathbf{P}, \mathbf{X})
&= \sum_{m = 1}^{M} \mathbf{A}_{m} \mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \right) \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
&= \sum_{m = 1}^{M} \text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \right)^{\top}}{\sqrt{C_v}} + \mathbf{b}_m \right) \mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \left(\mathbf{Z} \right)
\right) \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
&= \sum_{m = 1}^{M} \text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{X}\left( \mathbf{P} + f_{m} \left(\mathbf{Z} \right) \right)^{\top}}{\sqrt{C_v}} + \mathbf{b}_m \right) \mathbf{X}\left( \mathbf{P} + f_{m} \left(\mathbf{Z} \right)
\right) \mathbf{W}_m^{\prime \top} \mathbf{W}_m^{\top} \\
\end{aligned}
$$
where $\mathbf{Z} \in \mathbb{R}^{N_q \times C}$ and $\mathbf{P} \in \mathbb{R}^{N_q \times 2}$ are the query feature matrix and the reference point matrix, respectively, $\Delta\mathbf{P}_m \in \mathbb{R}^{N_q \times K \times 2}$ is the offset matrix for the $m$-th attention head, and $\mathbf{A}_{m} \in \mathbb{R}^{N_q \times K}$ is the attention weight matrix for the $m$-th attention head, and $\mathbf{W}^{\prime\prime}_{m} \in \mathbb{R}^{K \times 2 \times C}$ and $\mathbf{W}^{\prime\prime\prime}_{m} \in \mathbb{R}^{K \times C}$ are the learnable weight matrices for the $m$-th attention head.
Deformable Multi-Head Attention V2 Computational Complexity
Ignoring the computational complexity of the offset computation $f_{m} \left(\mathbf{Z} \right)$ and the feature map interpolation $\mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \right)$ for each head, the computational complexity of the deformable multi-head attention v2 for $N_q$ queries and $K$ sampled shared keys can be derived as follows:
$$
\begin{aligned}
O\left( M \left( \underbrace{O\left(KC_v C \right)}_{\mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m
\right) \mathbf{W}_m^{\prime \top} } + \underbrace{O( K C C_{v} ) + O( N_q C C_{v} ) + O(N_q K C_v) + O(N_q K) + O(K)}_{\text{softmax}\left( \frac{\mathbf{Z} \mathbf{U}_m^{\top} \mathbf{V}_m \mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \right)^{\top}}{\sqrt{C_v}} + \mathbf{b}_m \right) } + O(N_q K C_v) + O(N_q C C_v) \right) \right)
&= O\left( M \left( O( K C C_{v} ) + O( N_q C C_{v} ) + O( N_q K C_v ) \right) \right) \\
&= O( K C^2 ) + O( N_q C^2 ) + O( N_q K C ) \\
&= O( K C^2 + N_q C^2 + N_q K C ) \\
\end{aligned}
$$
Given the computed offsets $\Delta\mathbf{P}_m$ for each head, the computational complexity of feature map interpolation $\mathbf{X}\left( \mathbf{P} + \Delta\mathbf{P}_m \right)$ is $O(MKC)$. The offset computation $f_{m} \left(\mathbf{Z} \right)$ is usually a small neural network module. Suppose the computational cost of the offset computation is sufficiently small comparing to the other components in the deformable multi-head attention v2, the computational complexity of the deformable multi-head attention v2 for $N_q$ queries and $K$ sampled shared keys is just $O( K C^2 + N_q C^2 + N_q K C + MKC)$.
For the Transformer based computer vision model encoder, because all the attention layers are self-attention, $N_q = N_k = HW$ where $H$ and $W$ are the height and width of the feature map, respectively. The computational complexity of the deformable multi-head attention v2 is $O( K C^2 + N_q C^2 + N_q K C + MKC ) = O( K C^2 + H W C^2 + H W K C + MKC )$. If $K \ll HW$, $M \ll C$, and $M \ll HW$, which is usually the case, the computational complexity of the deformable multi-head attention v2 becomes $O( H W C^2 )$ and it is the same as the one in the deformable multi-head attention and is much cheaper than the one in the vanilla multi-head attention.
Although the deformable multi-head attention v2 was originally developed for the Transformer backbone in the ViT and might have not been used in the Transformer decoder, we could still derive the computational complexity of the deformable multi-head attention v2 in the Transformer decoder. In the self-attention layers, $N_q = N_k = N$, the computational complexity of the deformable multi-head attention v2 is $O( K C^2 + NC^2 + N^2 C + MKC )$. This computation complexity might be comparable to the one used in the vanilla multi-head attention and the one used in the deformable multi-head attention, which is $O( NC^2 + N^2 C )$. In the cross-attention layers, the computational complexity of the deformable multi-head attention v2 is $O( K C^2 + N C^2 + N K C + MKC )$. Because $K < HW$ and $N \ll HW$, this computation complexity is much cheaper than the one used in the vanilla multi-head attention, which is $O( HWC^2 + NHWC )$, and can be comparable to the one used in the deformable multi-head attention, which is $O( NK C^2 )$. Note that the magnitude of $K$ used in the deformable multi-head attention and the deformable multi-head attention v2 can be quite different.
References
Deformable Attention