Depth of Field
Introduction
The depth of field (DOF) is the distance between the nearest and the farthest objects that are in acceptably sharp focus in an image captured with a camera. By definition, a photo that has a shallow DOF has the main subject in focus, while the background and foreground are blurred, and a photo that has a deep DOF has most of the objects in focus.
When the photo captures a scene of a landscape, a deep DOF is usually preferred, because it can show the details of the whole scene. When the photo captures a portrait or a specific object of interest, a shallow DOF is usually preferred, because it can highlight the main subject and blur the background and foreground.
There are a few key factors that affect the DOF of a photo, including the aperture, the focal length, the distance between the camera and the subject. In this blog post, I would like to derive the DOF equation, which is a function of the aperture, the focal length, the distance between the camera and the subject.
Thin Lens Equation
The thin lens equation is the fundamental equation that is used for deriving the DOF equation.
Assuming the thickness of the lens is infinitely small, the thin lens equation
$$
\frac{1}{f} = \frac{1}{u} + \frac{1}{v}
$$
where $f$ is the focal length, $u$ is the object distance to the lens, $v$ is the image distance to lens.
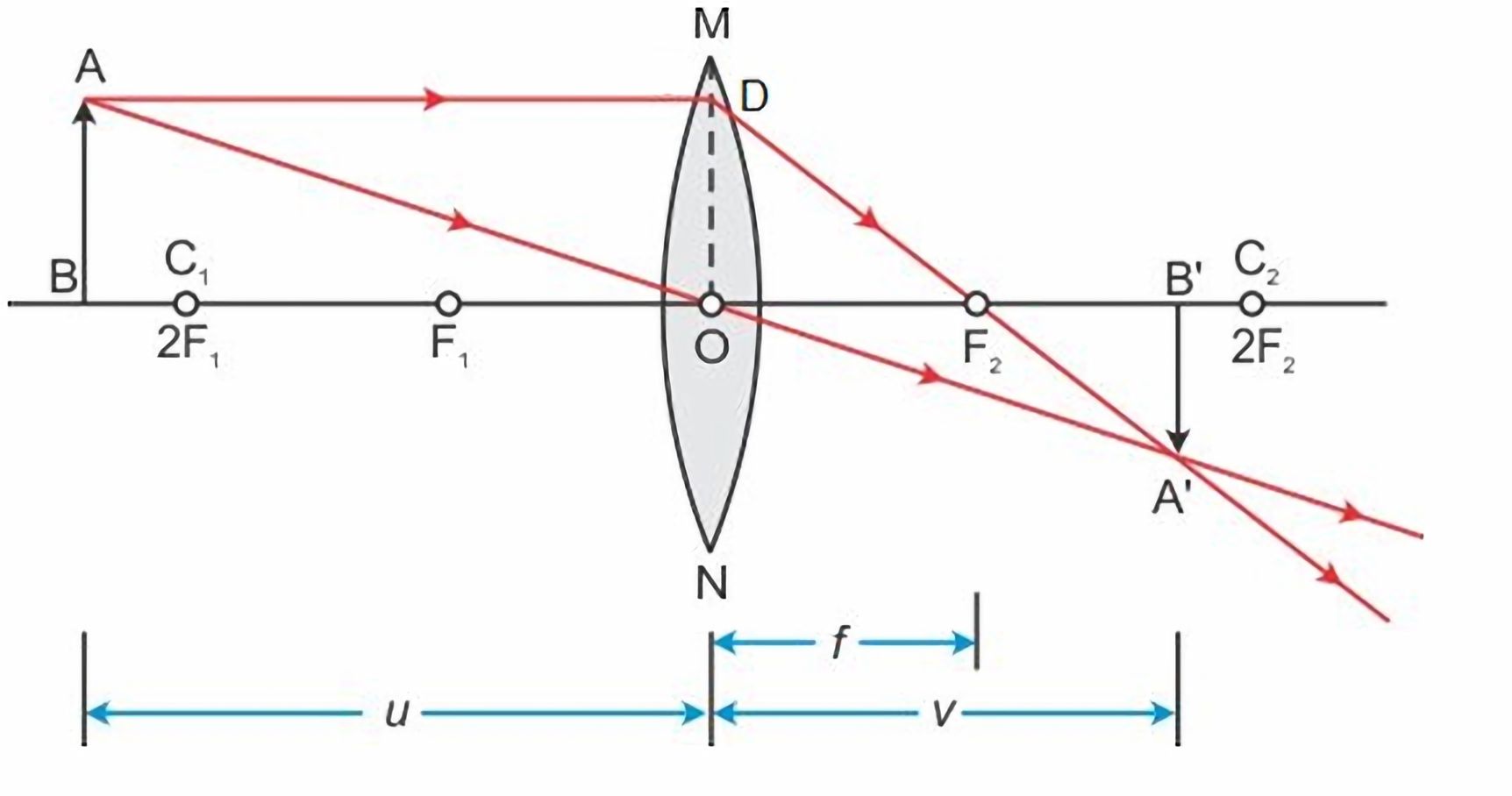
The proof of the thin lens equation can be found in my previous blog post “How Camera Lens Works”.
Circle of Confusion
In the above diagram, because the focal length $f$, the object distance to the lens $u$, the image distance to lens $v$ happen to satisfy the thin lens equation, the object $AB$ in the image plane, $A^{\prime}B^{\prime}$, is in focus and looks sharp.
But what if the thin lens equation is not satisfied, each point in the object $AB$ will be projected to a circle in the image plane instead of a perfect point. When the circle is small enough, our eyes cannot distinguish the circle from a point, and the object $AB$ still looks sharp in the image. However, when the circle is large enough, our eyes can distinguish the circle from a point, and the object $AB$ looks blurry in the image. The threshold of the circle size that our eyes can distinguish is called the circle of confusion $c$.
The diameter of the circle can be quantified mathematically.
Assuming the lens is set up in a way such that the focal length $f$ and the image distance to lens $v$ are fixed, and the object whose distance to the lens is $u$ is in focus.
Suppose there is another object $A_1B_1$ whose distance to the lens is $u_1$ and $u_1 > u$, to make this object in focus, the image distance to lens has to be $v_1$ and the thin lens equation has to be satisfied:
$$
\frac{1}{f} = \frac{1}{u_1} + \frac{1}{v_1}
$$
It is also straightforward to see that the image distance to lens $v_1 < v$.
Similarly suppose there is another object $A_2B_2$ whose distance to the lens is $u_2$ and $u_2 < u$, to make this object in focus, the image distance to lens has to be $v_2$ and the thin lens equation has to be satisfied:
$$
\frac{1}{f} = \frac{1}{u_2} + \frac{1}{v_2}
$$
It is also straightforward to see that the image distance to lens $v_2 > v$.
Because the image distance to lens $v$ is fixed, each point on the objects $A_1B_1$ and $A_2B_2$ and will be projected to circles in the image plane, and the diameters of the circles are $c_1$ and $c_2$ respectively.
Assuming the aperture $\left\vert MN \right\vert = a$, based on the simple geometry of similar triangles, the diameter of the circle $c_1$ and $c_2$ have the following equations.
$$
\frac{\frac{c_1}{2}}{\frac{a}{2}} = \frac{v - v_1}{v_1}
$$
$$
\frac{\frac{c_2}{2}}{\frac{a}{2}} = \frac{v_2 - v}{v_2}
$$
After some simplification, we have
$$
v_1 = \frac{av}{a + c_1}
$$
$$
v_2 = \frac{av}{a - c_2}
$$
Given the circle of confusion $c$, if the objects $A_1B_1$ and $A_2B_2$ still look sharp in the image, we must have
$$
v_1 = \frac{av}{a + c}
$$
$$
v_2 = \frac{av}{a - c}
$$
This means, as long as the object whose image distance to lens is within the range $\left[ \frac{av}{a + c}, \frac{av}{a - c} \right]$, the object will look sharp in the image.
For camera lens, it is more common to use $f$-stop, sometimes referred as $f$-number, instead of aperture to quantify the size of the aperture. The $f$-stop $A$ is defined as
$$
A = \frac{f}{a}
$$
Using the $f$-stop $A$ instead of the aperture $a$, the range of the image distance to lens that the object will look sharp in the image becomes
$$
v_1 = \frac{fv}{f + cA}
$$
$$
v_2 = \frac{fv}{f - cA}
$$
Accordingly, the range of the object distance to lens that the object will look sharp in the image can be computed using the thin lens equation.
$$
\begin{align}
u_1 &= \frac{1}{\frac{1}{f} - \frac{1}{v_1}} \\
&= \frac{1}{\frac{1}{f} - \frac{f + cA}{fv}} \\
&= \frac{1}{\frac{1}{f} - \frac{f + cA}{f} \left( \frac{1}{f} - \frac{1}{u} \right)} \\
&= \frac{1}{\frac{1}{f} - \frac{f + cA}{f} \frac{u -f}{fu}} \\
&= \frac{1}{\frac{1}{f} - \frac{\left(f + cA\right) \left(u -f\right)}{f^2 u}} \\
&= \frac{1}{\frac{fu}{f^2 u} - \frac{fu - f^2 + cA \left(u -f\right)}{f^2 u}} \\
&= \frac{1}{\frac{fu - fu + f^2 - cA \left(u -f\right)}{f^2 u}} \\
&= \frac{f^2 u}{f^2 - cA \left(u -f\right)} \\
\end{align}
$$
$$
\begin{align}
u_2 &= \frac{1}{\frac{1}{f} - \frac{1}{v_2}} \\
&= \frac{1}{\frac{1}{f} - \frac{f - cA}{fv}} \\
&= \frac{1}{\frac{1}{f} - \frac{f - cA}{f} \left( \frac{1}{f} - \frac{1}{u} \right)} \\
&= \frac{1}{\frac{1}{f} - \frac{f - cA}{f} \frac{u -f}{fu}} \\
&= \frac{1}{\frac{1}{f} - \frac{\left(f - cA\right) \left(u -f\right)}{f^2 u}} \\
&= \frac{1}{\frac{fu}{f^2 u} - \frac{fu - f^2 - cA \left(u -f\right)}{f^2 u}} \\
&= \frac{1}{\frac{fu - fu + f^2 + cA \left(u -f\right)}{f^2 u}} \\
&= \frac{1}{\frac{f^2 + cA \left(u -f\right)}{f^2 u}} \\
&= \frac{f^2 u}{f^2 + cA \left(u -f\right)} \\
\end{align}
$$
Depth of Field Equation
The depth of field (DOF) is the distance between the nearest and the farthest objects that are in acceptably sharp focus in an image captured with a camera. Therefore, based on the setup in the previous section, the DOF can be defined mathematically as
$$
\text{DOF} = u_1 - u_2
$$
Using the derived equations of $u_1$ and $u_2$, the DOF can be computed as
$$
\begin{align}
\text{DOF} &= u_1 - u_2 \\
&= \frac{f^2 u}{f^2 - cA \left(u -f\right)} - \frac{f^2 u}{f^2 + cA \left(u -f\right)} \\
&= \frac{f^2 u \left( f^2 + cA \left(u -f\right) \right)}{\left(f^2 - cA \left(u -f\right)\right) \left( f^2 + cA \left(u -f\right) \right)} - \frac{f^2 u \left( f^2 - cA \left(u -f\right) \right)}{\left(f^2 + cA \left(u -f\right)\right) \left( f^2 - cA \left(u -f\right) \right)} \\
&= \frac{f^2 u \left( f^2 + cA \left(u -f\right) \right) - f^2 u \left( f^2 - cA \left(u -f\right) \right)}{f^4 - c^2 A^2 \left(u -f\right)^2} \\
&= \frac{f^2 u f^2 + f^2 u cA \left(u -f\right) - f^2 u f^2 + f^2 u cA \left(u -f\right)}{f^4 - c^2 A^2 \left(u -f\right)^2} \\
&= \frac{2 f^2 u cA \left(u -f\right)}{f^4 - c^2 A^2 \left(u -f\right)^2} \\
\end{align}
$$
With some additional assumptions, this DOF equation can be simplified further to a form that we commonly see in photography.
Assuming $f \ll u \ll \frac{f^2}{cA}$, we have $u - f \approx u$ and $f^4 - c^2 A^2 \left(u -f\right)^2 \approx f^4$. Therefore, the DOF equation can be simplified as
$$
\text{DOF} = \frac{2 u^2 cA}{f^2}
$$
where $u$ is the distance between the camera and the object, $f$ is the focal length of the lens, $c$ is the circle of confusion, and $A$ is the $f$-stop.
Let’s also examine the feasibility of the assumption $f \ll u \ll \frac{f^2}{cA}$. For most of the lenses, the focal length $f$ is in the range of $10$ mm to $800$ mm and the $f$-stop $A$ is in the range of $1.4$ to $22$. The circle of confusion $c$ is usually in the range of $0.01$ mm to $0.03$ mm. So $\frac{f^2}{cA}$ is in a range of $\frac{10^2}{0.03 \times 1.4} \approx 2380$ mm to $\frac{800^2}{0.01 \times 22} \approx 2909090$ mm. Therefore, the assumption $f \ll u \ll \frac{f^2}{cA}$ is reasonable for most of the conventional photography scenarios.
Based on the simplified DOF equation, we can see that the DOF is proportional to the square of the distance between the camera and the object, the $f$-stop, and the circle of confusion, and inversely proportional to the square of the focal length of the lens.
Depth of Field Simulator
The Depth of Field Simulator created by Jack Herrington can be used for photographers to understand how the DOF changes with the distance between the camera and the object, the $f$-stop, the focal length of the lens. It essentially have applied the DOF equation we have derived in this article.
FAQs
Why Does Full Frame Camera Usually Have Shallower Depth of Field Than Crop Sensor Camera?
The full frame camera has a larger sensor size than the crop sensor camera. Therefore, the full frame camera usually has a longer focal length lens for the same field of view. According to the DOF equation, the DOF is inversely proportional to the square of the focal length of the lens. Therefore, the full frame camera usually has a shallower DOF than the crop sensor camera.
Why Does Cell Phone Camera Usually Have a Deep Depth of Field?
The cell phone camera usually has a small aperture (large $f$-stop) and a short focal length lens. According to the DOF equation, the DOF is proportional to the square of the focal length of the lens and inversely proportional to the square of the aperture. Therefore, the cell phone camera usually has a deep DOF. It will be very difficult for cell phone camera photographers to capture photos with very impressive blurred background and foreground.
Conclusions
In photography, because of the depth of field (DOF) equation, we have the following consequences.
- Moving the camera closer to the object can cause blurring in the background and foreground of the picture, producing a shallow DOF. Moving away from your subject has the opposite effect; the entire picture comes into focus, providing a deep DOF.
- Using a larger aperture (smaller $f$-stop) can cause blurring in the background and foreground of the picture, producing a shallow DOF. Using a smaller aperture (larger $f$-stop) has the opposite effect; the entire picture comes into focus, providing a deep DOF.
- Using a lens with a longer focal length can cause blurring in the background and foreground of the picture, producing a shallow DOF. Using a lens with a shorter focal length has the opposite effect; the entire picture comes into focus, providing a deep DOF.
To select lenses, we want to have longer focal length and smaller $f$-stop for shooting portraits and macro photography, and we want to have shorter focal length for shooting landscapes and architecture photography (usually we want the $f$-stop to be as smaller as possible for reducing the exposure time).
References
Depth of Field