Dropout Explained
Introduction
Dropout has been widely used in deep learning to prevent overfitting. Recently I found that I have misunderstood dropout for many years. I am writing this blog post to remind myself as well as all the people about the math and the caveats of dropout.
Dropout Implementations
Original Implementation
In the original implementation of dropout, dropout does work in both training time and inference time.
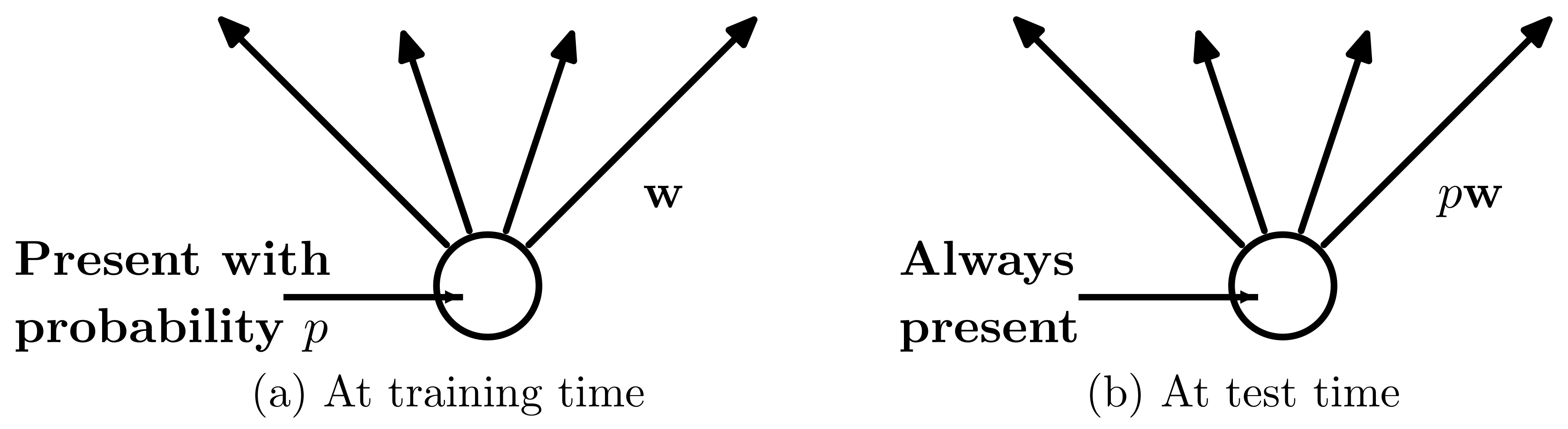
During training time, dropout randomly sets node values to zero. In the original implementation, we have “keep probability” $p_{\text{keep}}$. So dropout randomly kills node values with “dropout probability” $1-p_{\text{keep}}$. During inference time, dropout does not kill node values, but all the weights in the layer were multiplied by $p_{\text{keep}}$. One of the major motivations of doing so is to make sure that the distribution of the values after affine transformation during inference time is close to that during training time. Equivalently, This multiplier could be placed on the input values rather than the weights.
Concretely, say we have a vector $x = \{1,2,3,4,5\}$ as the input to certain fully connected layer and $p_{\text{keep}} = 0.8$. During training time, $x$ could be set to $\{1,0,3,4,5\}$ due to dropout. During inference time, $x$ would be set to $\{0.8,1.6,2.4,3.2,4.0\}$ while the weights remain unchanged.
Things are similar if you placed the multiplier to the output values rather than the input values or weights. However, in any of the implementations mentioned above, you have to make changes to the values in the neural network during both training time and inference time. This seems to be undesirable to TensorFlow. So TensorFlow has its own implementation of dropout which only does work during training time.
TensorFlow Implementation
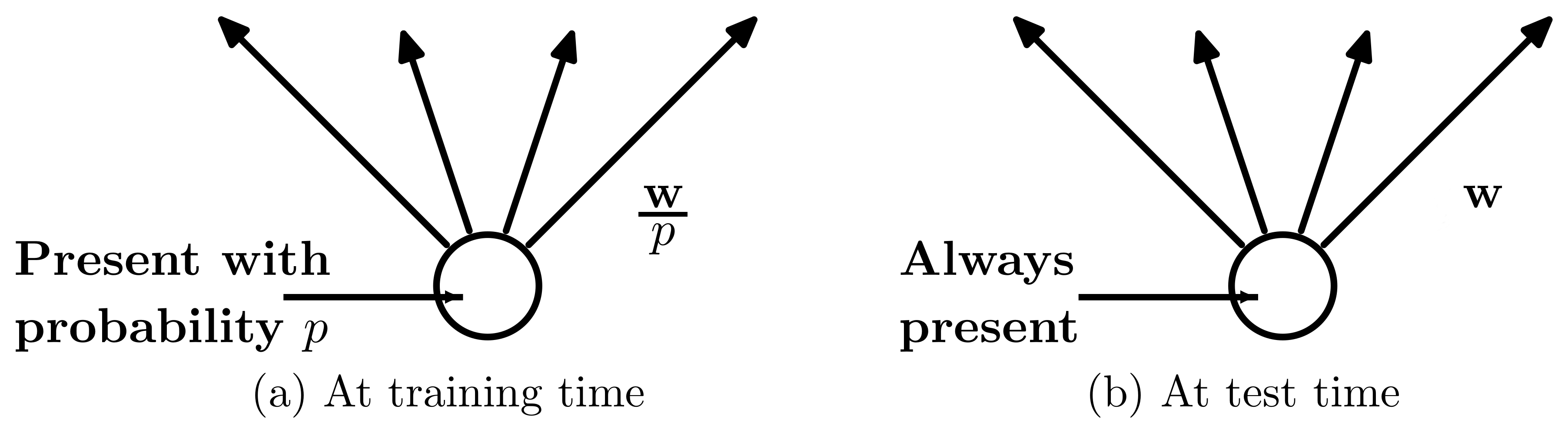
To avoid doing work during inference time, $p_{\text{keep}}$ has to be removed during inference time. To make sure that the distribution of the values after affine transformation during inference time remains almost the same, all the values that remains after dropout during training has to be multiplied by $\frac{1}{p_{\text{keep}}}$.
Concretely, say we have a vector $x = \{1,2,3,4,5\}$ as the input to certain fully connected layer and $p_{\text{keep}} = 0.8$. During training time, $x$ could be set to $\{1.25,0,3.75,5,6.25\}$ due to dropout. During test time, $x$ and the weights remain unchanged.
Equivalence?
Mathematically these two implementations do not look the same. These two are off by a constant value in both forward propagation and back propagation. However, regarding the optimization goal, these two implementations are equivalent, at least for linear regressions with mean square loss. Here I will show my proof below.
Let $X \in \mathbb{R}^{N \times D}$ be the data matrix, where $N$ is the number of data points, and $D$ is the number of features, $\mathbf{y} \in \mathbb{R}^{N}$ be the target values, and $\mathbf{w} \in \mathbb{R}^{D}$ be the weights. We have the following optimization goal.
$$
\min_{\mathbf{w}} ||\mathbf{y} - X\mathbf{w}||^2
$$
In the original dropout paper, the authors have shown that using their specific dropout implementation in this optimization task is equivalent to optimize the following formula.
$$
\min_{\mathbf{w}} ||\mathbf{y} - p_{\text{keep}} X \mathbf{w}||^2 + p_{\text{keep}} (1-p_{\text{keep}}) || \Gamma \mathbf{w}||^2
$$
where $\Gamma = (\text{diag}(X^T X))^{\frac{1}{2}}$
When we have a multiplier of $\frac{1}{p_{\text{keep}}}$ for $X$ during training, with dropout, it is equivalent to have the following optimization goal.
$$
\min_{\mathbf{w}} ||\mathbf{y} - p_{\text{keep}} X \frac{\mathbf{w}}{p_{\text{keep}}} ||^2 + p_{\text{keep}} (1-p_{\text{keep}}) || \Gamma \frac{\mathbf{w}}{p_{\text{keep}}}||^2
$$
Because $p_{\text{keep}}$ is a constant value, this is equivalent to optimize
$$
\min_{\frac{\mathbf{w}}{p_{\text{keep}}}} ||\mathbf{y} - p_{\text{keep}} X \frac{\mathbf{w}}{p_{\text{keep}}} ||^2 + p_{\text{keep}} (1-p_{\text{keep}}) || \Gamma \frac{\mathbf{w}}{p_{\text{keep}}}||^2
$$
It is further equivalent to optimize
$$
\min_{\mathbf{w}} ||\mathbf{y} - p_{\text{keep}} X \mathbf{w}||^2 + p_{\text{keep}} (1-p_{\text{keep}}) || \Gamma \mathbf{w}||^2
$$
Assume the optimal $\mathbf{w}$ from the original dropout implementation is $\mathbf{w}^{\ast}_{\text{original}}$ and the optimal $\mathbf{w}$ from the TensorFlow dropout implementation is $\mathbf{w}^{\ast}_{\text{TensorFlow}}$. It is not hard to see that
$$
\mathbf{w}^{\ast}_{\text{original}} = \frac{ \mathbf{w}^{\ast}_{\text{TensorFlow}} }{p_{\text{keep}}}
$$
The outputs of the two implementations are also identical given their optimal $\mathbf{w}$.
Therefore, the two implementations are equivalent, at least for linear regressions with mean square loss.
More General Equivalence?
In the forward propagation of the TensorFlow dropout implementation during training time, it is equivalent to multiply all the weights in the layer by $\frac{1}{p_{\text{keep}}}$ while keeping all the inputs unchanged.
We can see that for whatever optimization goal with the respect to $\mathbf{w}$, it is equivalent to optimize with the respect to $\frac{\mathbf{w}}{p_{\text{keep}}}$. It is also not hard to see that
$$
\mathbf{w}_{\text{original}}^{\ast} = \frac{ \mathbf{w}_{\text{TensorFlow}}^{\ast} }{p_{\text{keep}}}
$$
The outputs of the two implementations are also identical given their optimal $\mathbf{w}$.
The conclusion is that the two dropout implementations are identical.
Dropout in Convolutional Neural Network
The original dropout was discussed in the scope of fully connected layers. But dropout in convolutional layers is hardly seen. There are some debates about the dropout effects in convolutional neural networks.
Some people think dropout should not be used in convolutional layers because convolutional layers have fewer parameters and are less likely to overfit. Because the gradient updates for the weights of convolutional layers are the average of all the gradients from all the convolutions, randomly killing nodes will slow down the training process.
In my opinion, dropout does provide regularization for any kind of neural network architectures. It also provides additional benefits from the perspective of Bayesian learning, which I might discuss in the future. But in practice, depending on the task, dropout may or may not affect the accuracy of your model. If you want to apply dropout in convolutional layers, just make sure that you test the training with and without dropout to see if it makes a difference.
Caveats
- It should be noted that doing dropout during inference time is equivalent to doing dropout during training time with $p_{\text{keep}} = 1.0$.
- In general, the order of the layers is X -> Dropout Layer -> Fully Connected Layer -> Activation Layer, where X could be any layer.
References
Dropout Explained