Transformer Explained In One Single Page
Introduction
Transformer is one of the most influential sequence transduction models as it is based solely on attention mechanisms dispensing recurrence and convolutions. Previously deep learning sequence transduction models usually consist of recurrence architecture which could hardly take advantage of modern parallel computing. With recurrence removed, Transformer showed not only training performance gain but also better results in machine translation compared to state of the art in 2017.
After going through the architecture of Transformer, I found that it is actually simple mathematically, probably due to the lack of recurrence and convolutions. In this blog post, I will try to illustrate the Transformer model mathematically in one single page.
Overview
Model Architecture
I have to admit that for the first time I read the Transformer paper “Attention is All You Need”, I did not understand the model thoroughly. This was probably because I have not been studying natural language processing for many years. There is a very good blog post from Jay Alammar illustrating how Transformer works with animated gifs. It helped me understand the model quite well.
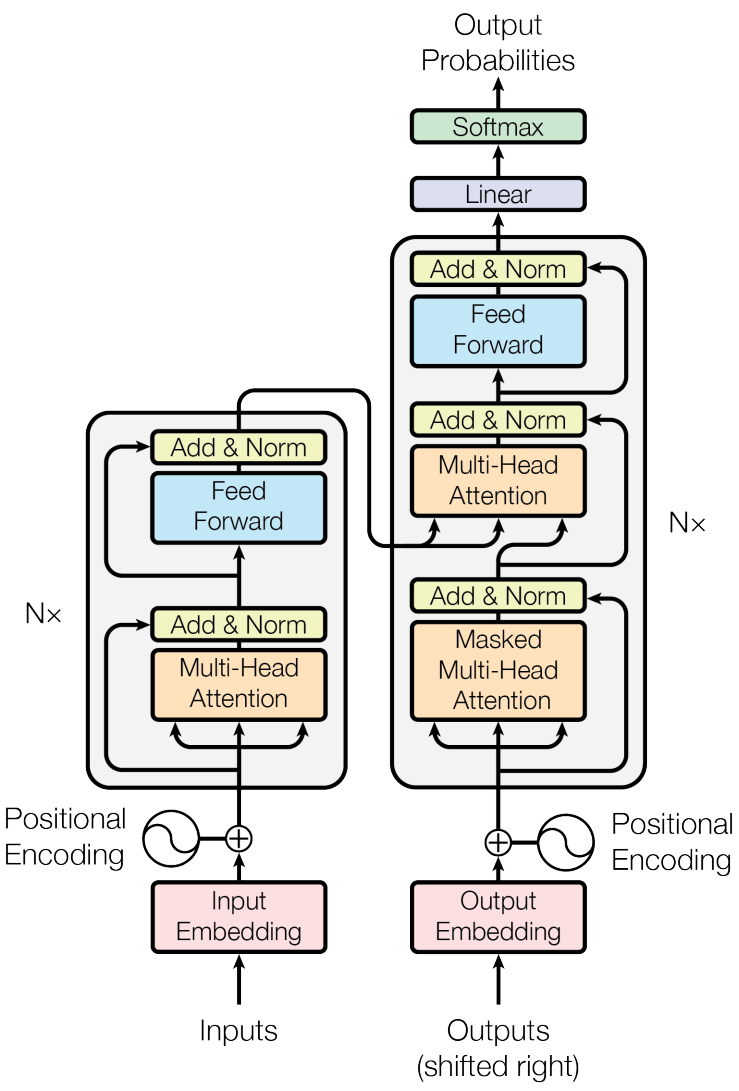
Later I found explaining Transformer using mathematics is much easier and concise, and causes less confusion about the model for the beginners.
Machine Translation
I will use the machine translation example from Jay Alammar in my blog post. We have an input in French “je suis étudiant”, and the translation program translates it to “i am a student” in English. I am using this French-to-English translation as an example in particular because the number of input words is different from the number of output words, and I want to make use of that to help the readers understand with less confusion.
Mathematical Formulations
Variables
These are all the variables we would use in the Transformer model.
$n_\text{input}$: number of input words (embeddings).
$n_\text{output}$: number of output words (embeddings).
$N$: number of stacks in the encoder, the number of stacks in the decoder.
$d_\text{model}$: length of word embedding vector.
$d_k$: length of query vector, length of the key vector.
$d_v$: length of value vector.
$d_{ff}$: length of the inner layer of feedforward networks
$h$: number of attention heads in multi-head attention.
$n_\text{vol}$: vocabulary size.
$W_{\text{Embedding}} \in \mathbb{R}^{n_\text{vol} \times d_\text{model}}$: word embedding matrix.
$W_{i,j}^{Q,E} \in \mathbb{R}^{d_\text{model} \times d_k}$: linear transformation matrix for queries in attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$W_{i,j}^{K,E} \in \mathbb{R}^{d_\text{model} \times d_k}$: linear transformation matrix for keys in attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$W_{i,j}^{V,E} \in \mathbb{R}^{d_\text{model} \times d_v}$: linear transformation matrix for values in attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$W_{i}^{O,E} \in \mathbb{R}^{h d_v \times d_\text{model}}$: linear transformation matrix for concatenated attention heads of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$W_{i,j}^{Q,D} \in \mathbb{R}^{d_\text{model} \times d_k}$: linear transformation matrix for queries in attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,j}^{K,D} \in \mathbb{R}^{d_\text{model} \times d_k}$: linear transformation matrix for keys in attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,j}^{V,D} \in \mathbb{R}^{d_\text{model} \times d_v}$: linear transformation matrix for values in attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i}^{O,D} \in \mathbb{R}^{h d_v \times d_\text{model}}$: linear transformation matrix for concatenated attention heads of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,j}^{Q,DM} \in \mathbb{R}^{d_\text{model} \times d_k}$: linear transformation matrix for queries in masked attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,j}^{K,DM} \in \mathbb{R}^{d_\text{model} \times d_k}$: linear transformation matrix for keys in masked attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,j}^{V,DM} \in \mathbb{R}^{d_\text{model} \times d_v}$: linear transformation matrix for values in masked attention head $j \in \{ 1, 2, \cdots, h \}$ of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i}^{O,DM} \in \mathbb{R}^{h d_v \times d_\text{model}}$: linear transformation matrix for concatenated masked attention heads of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,1}^{FF,E} \in \mathbb{R}^{d_\text{model} \times d_{ff}}$: linear transformation matrix to the inner layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$b_{i,1}^{FF,E} \in \mathbb{R}^{d_{ff}}$: bias term to the inner layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$W_{i,2}^{FF,E} \in \mathbb{R}^{d_{ff} \times d_{\text{model}}}$: linear transformation matrix to the output layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$b_{i,2}^{FF,E} \in \mathbb{R}^{d_{\text{model}}}$: bias term to the output layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the encoder.
$W_{i,1}^{FF,D} \in \mathbb{R}^{d_\text{model} \times d_{ff}}$: linear transformation matrix to the inner layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$b_{i,1}^{FF,D} \in \mathbb{R}^{d_{ff}}$: bias term to the inner layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W_{i,2}^{FF,D} \in \mathbb{R}^{d_{ff} \times d_{\text{model}}}$: linear transformation matrix to the output layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$b_{i,2}^{FF,D} \in \mathbb{R}^{d_{\text{model}}}$: bias term to the output layer in the feed forward network of stack $i \in \{ 1, 2, \cdots, N \}$ in the decoder.
$W^{S} \in \mathbb{R}^{d_{\text{model}} \times n_\text{vol}}$: linear transformation matrix to the final softmax layer after decoder.
$b^{S} \in \mathbb{R}^{n_\text{vol}}$: bias term to to the final softmax layer after decoder.
Functions
These are all the functions we would use in the Transformer model.
To calculate the embeddings after attention,
$$
\text{Attention}(Q,K,V) = \text{softmax}\big(\frac{QK^{\top}}{\sqrt{d_k}}\big)V
$$
For encoder multi-head attention for stack $i$ in the encoder,
$$
\text{MultiHead}_{i}^{E} (Q,K,V) = \text{Concat}(\text{head}_{i,1}^{E}, \text{head}_{i,2}^{E}, \cdots, \text{head}_{i,h}^{E})W_{i}^{O,E}
$$
where
$$
\text{head}_{i,j}^{E} = \text{Attention}(QW_{i,j}^{Q,E}, KW_{i,j}^{K,E}, VW_{i,j}^{V,E})
$$
Similarly, for decoder multi-head attention for stack $i$ in the decoder,
$$
\text{MultiHead}_{i}^{D} (Q,K,V) = \text{Concat}(\text{head}_{i,1}^{D}, \text{head}_{i,2}^{D}, \cdots, \text{head}_{i,h}^{D})W_{i}^{O,D}
$$
where
$$
\text{head}_{i,j}^{D} = \text{Attention}(QW_{i,j}^{Q,D}, KW_{i,j}^{K,D}, VW_{i,j}^{V,D})
$$
Masked multi-head attention only exists in the decoder. For the masked multi-head for stack $i$ in the decoder during training.
$$
\text{MaskedMultiHead}_{i}^{T} (Q,K,V) = \text{Concat}(\text{head}_{i,1}^{DM}, \text{head}_{i,2}^{DM}, \cdots, \text{head}_{i,h}^{DM})W_{i}^{O,DM}
$$
where
$$
\text{head}_{i,j}^{DM} = \text{softmax} \bigg( \text{Mask} \big( \frac{ (QW_{i,j}^{Q,DM}) (KW_{i,j}^{K,DM})^{\top}}{\sqrt{d_k}} \big) \bigg)(VW_{i,j}^{V,DM})
$$
$\text{Mask}(x)$ is a function which takes a square matrix $x$ as input. We have $x’ = \text{Mask}(x)$ where
$$
x’_{i,j} =
\begin{cases}
x_{i,j} & \text{if } i \geq j \\
-\infty & \text{otherwise}
\end{cases}
$$
$\text{LayerNorm}$ is a normalization layer which does not change the shape of tensors. Please find the details of layer normalization in one of my blog posts.
For feed forward neural network for stack $i$ in the encoder,
$$
\text{FFN}_{i}^{E}(x) = \max(0, x W_{i,1}^{FF,E} + b_{i,1}^{FF,E}) W_{i,2}^{FF,E} + b_{i,2}^{FF,E}
$$
Similarly, for feed forward neural network for stack $i$ in the decoder,
$$
\text{FFN}_{i}^{D}(x) = \max(0, x W_{i,1}^{FF,D} + b_{i,1}^{FF,D}) W_{i,2}^{FF,D} + b_{i,2}^{FF,D}
$$
For positional encoding, $\text{PE}$ takes a two dimensional $x \in \mathbb{R}^{n \times d_\text{model}}$ matrix as input, we have $x’ \in \mathbb{R}^{n \times d_\text{model}}$ and $x’ = \text{PE}(x)$ where
$$
x’_{i,j} =
\begin{cases}
\sin \big( \frac{i}{10000^{j / d_\text{model}}} \big) & \text{if } j\mod 2 = 0 \\
\cos \big( \frac{i}{10000^{(j-1) / d_\text{model}}} \big) & \text{otherwise}
\end{cases}
$$
Training Phase
Let us first look at the encoder.
We have an input consisting of $n_\text{input}$ words, the input matrix $X_{\text{input}} \in \mathbb{R}^{n_\text{input} \times n_\text{vol}}$ has $X_{\text{input}} = \{x_1, x_2, \cdots, x_{n_\text{input}}\}$. Each $x_k$ is a one-hot encoded row vector of length $n_\text{vol}$ for the corresponding word.
Then we have the input embedding matrix $X \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$:
$$
X = \sqrt{d_\text{model}} X_{\text{input}} W_{\text{Embedding}}
$$
We further add positional encoding to the embedding matrix resulting in matrix $X’ \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$.
$$
X’ = \text{PE}(X) + X
$$
Here we started to apply self-attention! $Z_{1,1}^{E} \in \mathbb{R}^{n_{\text{input}} \times d_\text{model}}$
$$
Z_{1,1}^{E} = \text{MultiHead}_{1}^{E}(X’,X’,X’)
$$
We use residual connection and apply layer normalization, $Z_{1,2}^{E} \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$
$$
Z_{1,2}^{E} = \text{LayerNorm}(X’ + Z_{1,1}^{E})
$$
Then we do feed forward neural network, $Z_{1,3}^{E} \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$
$$
Z_{1,3}^{E} = \text{FFN}_{1}^{E}(Z_{1,2}^{E})
$$
We use residual connection and apply layer normalization, $Z_{1,4}^{E} \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$
$$
Z_{1,4}^{E} = \text{LayerNorm}(Z_{1,2}^{E} + Z_{1,3}^{E})
$$
$Z_{1,4}^{E}$ will be used as the input to the next stack (stack 2) in the encoder, $Z_{2,1}^{E} \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$
$$
Z_{2,1}^{E} = \text{MultiHead}_{2}^{E}(Z_{1,4}^{E},Z_{1,4}^{E},Z_{1,4}^{E})
$$
We iterate this process $N$ times, and get $Z_{N,4}^{E} \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$ from the stack $N$ in the encoder. This encoded embeddings $Z_{N,4}^{E}$ will be used for each of the stacks in the decoder.
We then look at the decoder.
We have the translation output, which is the translation of input, consisting of $n_{\text{output}}$ words. the output matrix $Y_{\text{output}} \in \mathbb{R}^{n_{\text{output}} \times n_{\text{vol}}}$ has $Y_{\text{output}} = \{ y_1, y_2, \cdots, {y_{n_{\text{output}}}} \}$. Each $y_k$ is a one-hot encoded row vector of length $n_\text{vol}$ for the corresponding word.
The input to the decoder the right shifted of ${Y_{\text{output}}}$, ${Y_{\text{output}}^{\prime}}$. Concretely ${Y_{\text{output}}^{\prime}} = \{ y_0, y_1, y_2, \cdots, {y_{n_{\text{output}}-1}} \}$, and $y_0$ could just simply be a zero vector.
Given ${Y_{\text{output}}^{\prime}}$, we wish to the decoder could generate ${Y_{\text{output}}}$.
Similar to the encoder, we have the output embedding matrix $Y \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$:
$$
Y = \sqrt{d_\text{model}} Y_{\text{output}}^{\prime} W_{\text{Embedding}}
$$
We further add positional encoding to the embedding matrix resulting in matrix $Y’ \in \mathbb{R}^{n_\text{input} \times d_\text{model}}$.
$$
Y’ = \text{PE}(Y) + Y
$$
Then we started to apply self-attention. However, in order to prevent the current word input to peek the following words, we used masked multi-head attention instead of the ordinary multi-head attention we used in the encoder. Here is the intuition. During training, the full right shifted output ${Y_{\text{output}}^{\prime}}$ was fed. Without the mask, after applying self-attention, word $y_i$ will have attention to word $y_j$ for $j > i$. This is unwanted. By applying mask, the attention of word $y_i$ to word $y_j$ for $j > i$ will be 0. We have $Z_{1,1}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$
$$
Z_{1,1}^{D} = \text{MaskedMultiHead}_{1}^{T}(Y’,Y’,Y’)
$$
We use residual connection and apply layer normalization, $Z_{1,2}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$
$$
Z_{1,2}^{D} = \text{LayerNorm}(Y’ + Z_{1,1}^{D})
$$
Then we use queries from $Z_{1,2}^{D}$, keys and values from $Z_{N,4}^{E}$. We then do multi-head attention trying to find the attention of the words to the embeddings from the encoder. $Z_{1,3}^{D} \in \mathbb{R}^{n_{\text{output}} \times d_\text{model}}$
$$
Z_{1,3}^{D} = \text{MultiHead}_{i}^{D} (Z_{1,2}^{D}, Z_{N,4}^{E}, Z_{N,4}^{E})
$$
We use residual connection and apply layer normalization, $Z_{1,4}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$
$$
Z_{1,4}^{D} = \text{LayerNorm}(Z_{1,2}^{D} + Z_{1,3}^{D})
$$
Then we do feed forward neural network, $Z_{1,4}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$
$$
Z_{1,5}^{D} = \text{FFN}_{1}^{D}(Z_{1,4}^{D})
$$
We use residual connection and apply layer normalization, $Z_{1,6}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$
$$
Z_{1,6}^{D} = \text{LayerNorm}(Z_{1,4}^{D} + Z_{1,5}^{D})
$$
$Z_{1,6}^{D}$ will be used as the input to the next stack (stack 2) in the decoder, $Z_{2,1}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$
$$
Z_{2,1}^{D} = \text{MaskedMultiHead}_{2}^{T}(Z_{1,6}^{D}, Z_{1,6}^{D}, Z_{1,6}^{D})
$$
We iterate this process $N$ times, and get $Z_{N,6}^{D} \in \mathbb{R}^{n_\text{output} \times d_\text{model}}$ from the stack $N$ in the decoder. This encoded embeddings $Z_{N,6}^{D}$ will be used for linear transformation followed by softmax to generate the output probabilities for the decoded word sequence. Concretely, we have $Z \in \mathbb{R}^{n_\text{output} \times n_\text{vol}}$ where
$$
Z = Z_{N,6}^{D} W^{S} + b^{S}
$$
We then apply softmax to get the probability matrix $P \in \mathbb{R}^{n_\text{output} \times n_\text{vol}}$ where
$$
P = \text{softmax}(Z)
$$
Finally we could calculate the cross entropy loss using $Y$ and $P$. More specifically, each row of $Y_{\text{output}}$ and $P$ are $y_i$ and $p_i$ respectively.
$$
L = \sum_{i=1}^{n_\text{output}} \text{CrossEntropy}(y_i, p_i)
$$
Inference Phase
To predict the $k$th word in translation, we need to feed the previous $k-1$ predicted word to the decoder and get the new predictions of the first $k$ words. We iterate this step until a stop sign word is predicted.
There has been a “debate” whether the attention mask used in the masked multi-head attention in the decoder during training should also be used during inference, probably because the way of describing the attention mask is a little bit confusing in the original paper. Frankly speaking, at first I thought we would not need such attention mask during inference, but I was wrong.
The attention mask was used in the masked multi-head attention during training to prevent the tokens from peaking or attending to the future predicted tokens. This is usually not difficult to understand. During inference, there is no future predicted tokens to peak, which naturally leads to the thought that we would not need such attention mask anymore. Not using the attention mask will, however, leads to the training and inference behavior difference and causes accuracy drop during inference. Notice that it is a little bit strange that with the attention mask during the inference, given a decoding sequence of length $n$, to predict the token $n + 1$, the token $i$ can only attend to the tokens $0$, $1$, $\cdots$, $i$, but not the tokens $i + 1$, $i + 2$, $\cdots$, $n$. However, this is the training behavior.
What’s more, by using the attention mask during the autoregressive inference, once the token $i$ is predicted, it will never change in the following autoregressive token predictions. To optimize the Transformer autoregressive inference, the intermediate tensors of the predicted tokens at the previous time step can be cached and used for the token prediction at the current time step, which significantly reduced the inference cost because all the values related to the previous tokens does not have to be recalculated.
One can image that without using the attention mask during the autoregressive inference, once the token $i$ is predicted, it can change in the following autoregressive token predictions, which causes prediction chaoses.
Concrete Example
In the training phase, we have the following translation to train, “je suis étudiant” -> “i am a student”. We first feed “je suis étudiant” all together into the encoder and get its keys and values. Then we feed “$\emptyset$ i am a” all together into the decoder and get the final probabilities to calculate the cross entropy loss.
In the test phase, we have the following French sentence to translate, say, again “je suis étudiant”. We first feed “je suis étudiant” all together into the encoder and get it keys and values. To get the first translation word, we feed “$\emptyset$” into the decoder and get the first word prediction, say “he” (note that this translation is “incorrect”). To get the second translation word, we feed “$\emptyset$ he” into the decoder and get the new prediction for the first word, say, “he” (note that this error will not be corrected in the autogressive predictions because the reasons we mentioned above), and the prediction for the second word, say, “am”. To get the third translation word, we feed “$\emptyset$ he am” into the decoder and get the new prediction for the first word, say, “he”, and the new prediction for the second word, say, “am”, and the prediction for the third word, say, “a”. We iterate until at some time point a stop sign word is predicted. A valid translation could be “he am a good student $\times$”.
Notice that this inference can be optimized in a way that every time step we only feed one token and predict one token by using the caching optimization mentioned previously.
References
Transformer Explained In One Single Page