Focus In Landscape Photography

Introduction

Unlike portrait photography and wildlife photography, landscape photography often requires a large depth of field to keep the entire scene looking sharp.

In this article, I would like to quickly discuss the focus techniques for landscape photography theoretically.

Thin Lens Equation

The thin lens equation is the fundamental equation that is used for deriving the DOF equation.

Assuming the thickness of the lens is infinitely small, the thin lens equation

$$
\frac{1}{f} = \frac{1}{u} + \frac{1}{v}
$$

where $f$ is the focal length, $u$ is the object distance to the lens, $v$ is the image distance to lens.

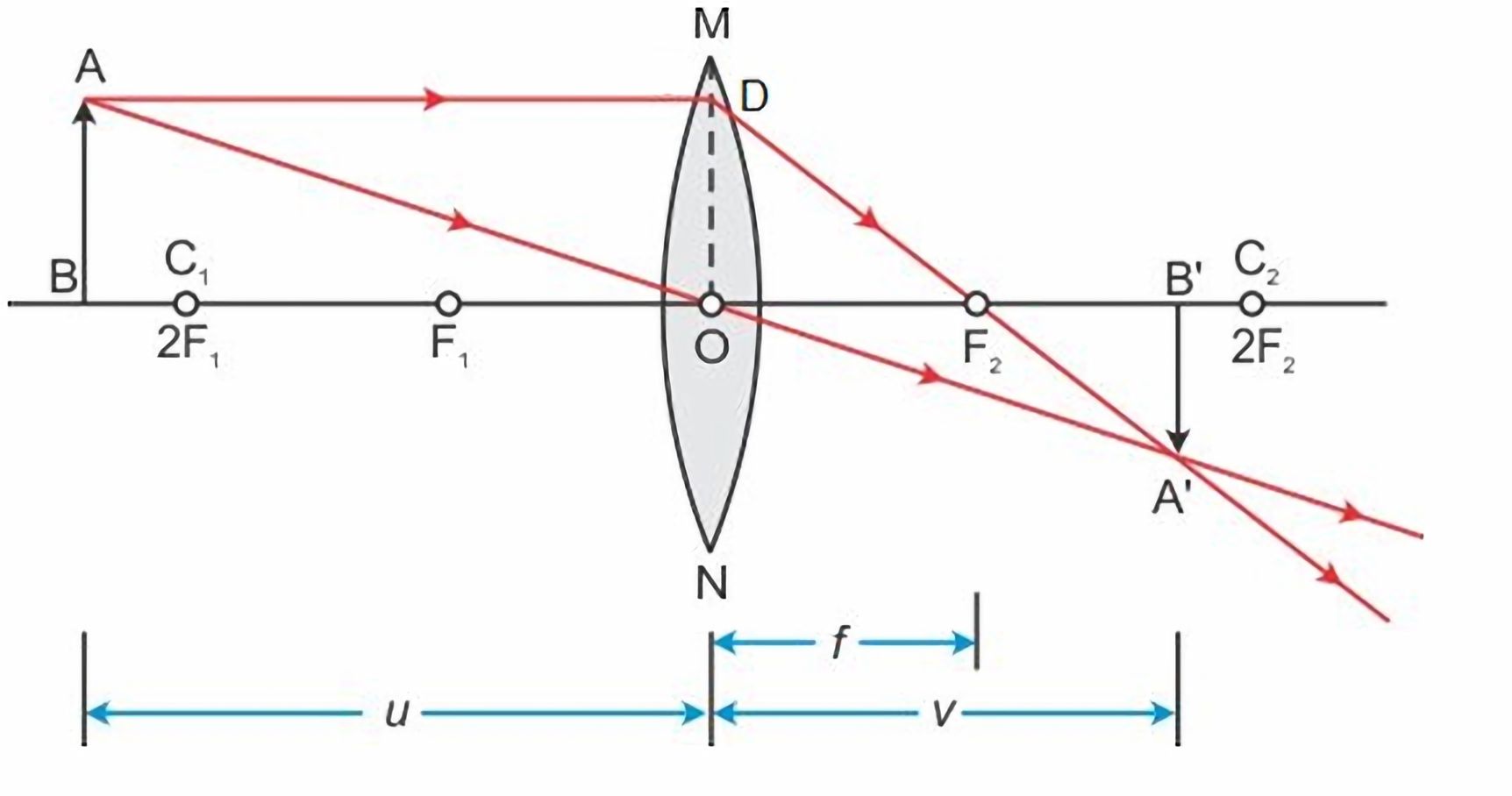
The proof of the thin lens equation can be found in my previous blog post “How Camera Lens Works”.

Focus In Landscape Photography

Depth of Field Equation

Previously, I have derived the depth of field (DOF) equation in my article “Depth of Field”. The depth of field can be calculated using the following equation:

$$
\begin{align}
\text{DOF}
&= \frac{2 f^2 u cA \left(u -f\right)}{f^4 - c^2 A^2 \left(u -f\right)^2} \\
\end{align}
$$

where $f$ is the focal length, $u$ is the distance to the subject, $c$ is the circle of confusion, and $A$ is the $f$-stop.

Depth of Field Equation for Landscape Photography

In landscape photography, usually we will use wide-angle lenses whose focal lengths are relatively small, and the distance to the subject is much larger than the focal length. Therefore, we have $u \gg f$ and $u -f \approx u$. For example, if we are using a 16 mm lens to focus on a point that is 1.6 m away, $u = 1000 f$ and $u - f \approx u$. In this case, the denominator of the depth of field equation can be approximated as:

$$
\begin{align}
f^4 - c^2 A^2 \left(u -f\right)^2 &\approx f^4 - c^2 A^2 u^2 \\
&= f^4 \left(1 - \frac{c^2 A^2 u^2}{f^4}\right) \\
\end{align}
$$

Usually $c = 0.01 - 0.03$ mm, $A = 2.8 - 22$, $f = 12 - 35$ mm, and $u > 1000 f$ for landscape photography, so we have $\frac{c^2 A^2 u^2}{f^4} \gg 1$ and $f^4 - c^2 A^2 \left(u -f\right)^2 < 0$. This means that $\text{DOF} < 0$, which does not make sense. Consequently, we could not use the depth of field equation directly for landscape photography.

Deriving Depth of Field for Landscape Photography

We should take one step back and look at how the depth of field equation was derived.

In my previous derivation, we have

$$
\begin{align}
v_{1} &= \frac{f v}{f + c A} \\
v_{2} &= \frac{f v}{f - c A} \\
\end{align}
$$

where $v_{1}$ and $v_{2}$ are the image distances to lens for the near and far objects that look sharp near the object in focus, respectively, $f$ is the focal length, $v$ is the image distance to lens, $c$ is the circle of confusion, and $A$ is the $f$-stop and $A = \frac{f}{a}$, where $a$ is the aperture.

$$
\begin{align}
u_{1} &= \frac{f^2 u}{f^2 - c A (u - f)} \\
u_{2} &= \frac{f^2 u}{f^2 + c A (u - f)} \\
\end{align}
$$

where $u_{1}$ and $u_{2}$ are the object distances to lens for the near and far objects that look sharp near the object in focus, respectively, and $u$ is the distance to the object in focus.

The DOF can be defined mathematically as

$$
\text{DOF} = u_1 - u_2
$$

Using the thin lens equation,

$$
\frac{1}{f} = \frac{1}{u} + \frac{1}{v}
$$

Because $u \gg f$ in landscape photography, we must have $v \approx f$. Therefore, it is quite possible that $v_{1} = \frac{f v}{f + c A} < f$.

We used the thin lens equation to compute the object distance $u_{1}$ for the far object that looks sharp.

$$
\frac{1}{f} = \frac{1}{u_{1}} + \frac{1}{v_{1}}
$$

However, because $v_{1} < f$, $u_{1}$ becomes negative, which does not make sense.

Therefore, before computing the object distance $u_{1}$, we should first compute the image distance $v_{1}$ to see if $v_{1} < f$.

• If $v_{1} < f$, we will just set $v_{1} = f$ and $u_{1} = \infty$.
• If $v_{1} \geq f$, we can compute $u_{1}$ using the thin lens equation, and $u_{1} = \frac{f^2 u}{f^2 - c A (u - f)}$.

In landscape photography, because $u \gg f$, we have $u_{1} = \infty$ in most of the cases. This means that the far objects that will always look sharp at infinity, which is what we want in landscape photography.

In some rare cases where we really want to focus on something close, we have $u_{1} = \frac{f^2 u}{f^2 - c A (u - f)}$, we could increase the $f$-stop to make the depth of field larger.

How about the near object? We have $u_{2} = \frac{f^2 u}{f^2 + c A (u - f)}$.

In landscape photography, because $u \gg f$, we have $u_{2} \approx \frac{f^2 u}{f^2 + c A u}$. In most of the cases, $c A u \gg f^2$, so we have $u_{2} \approx \frac{f^2 u}{c A u} = \frac{f^2}{c A}$.

Let’s see what the value of $u_{2}$ typically is in landscape photography. As I mentioned before, $c = 0.01 - 0.03$ mm, $A = 2.8 - 22$, and $f = 12 - 35$ mm. Therefore, we have

$$
\begin{align}
u_{2} \approx \frac{f^2}{c A}
&< \frac{35^2}{0.01 \times 2.8} \text{mm} \\
&= 4375 \text{mm} \\
&= 4.375 \text{m} \\
\end{align}
$$

Therefore, in landscape photography, the all the objects that are farther than 4.375 m away from the camera will always be sharp, provided that the $u \gg f$.

In some rare cases where we really want to focus on something close, we have $u_{2} = \frac{f^2 u}{f^2 + c A (u - f)}$, we could increase the $f$-stop to make the depth of field larger because $u_{2}$ becomes smaller, the things that are close to the camera will become sharper, and the depth of field $\text{DOF} = u_{1} - u_{2}$ becomes larger.

Conclusions

We could get infinite depth of field in landscape photography as long as we don’t focus on objects that are very close to the camera. Typically, focusing on an object whose $u > 1000 f$ will give us a good depth of field.

If we really have to focus on something close, we could increase the $f$-stop to make the depth of field larger.

References

• Depth of Field