Population Based Training
Introduction
Training a machine learning model often requires a lot of hyperparameters, such as learning rate and regularization strength. The initial values of the hyperparameters and optionally how the hyperparameters are dynamically tuned during training would have a huge impact on the performance of the optimized model.
Given the combination of hyperparameter schedules are usually infinite, it is often not possible to do exhaustive search to find the best hyperparameter schedule for optimization, even with a lot of computer resources. Instead, what people often do is do hyperparameter grid search to some extent and optionally further fine-tune hyperparameters based on experience with a little bit more trials. While such method works well in practice, it requires a lot of human intervention and possibly miss a better model. Therefore, finding good hyperparameters and hyperparameter tuning approaches during optimization become critical for modeling.
In this blog post, I would like to discuss the population based training, with a genetic algorithm inspired hyperparameter tuning schedule, proposed by DeepMind.
Machine Learning Optimization Theories
Mathematically, a model consists of model parameters $\theta$, and our goal is to maximize or minimize an evaluation objective $Q(\theta)$. Typically, this $Q(\theta)$ already contains the entire model, the validation data, and a performance metric. For example, the evaluation objective for machine translation could be applying the validation data to the model, getting the outputs from the model, and compute the BLEU score, the performance metric, using the model outputs and ground truth labels. The evaluation objective $Q(\theta)$ does not have to be differentiable with respect to the model parameters $\theta$, and sometimes it could even be a black-box!
To maximize or minimize an evaluation objective $Q(\theta)$, we would need to find the optimized model parameters $\theta$, using some optimization techniques. In practice, we don’t want to use the evaluation objective for optimization, or the evaluation objective $Q(\theta)$ could not be directly used for optimization. For instance, the evaluation objective uses validation data and if we use the evaluation objective for optimization, the generalization of the optimized model would be usually poor in practice. Another common obstacle is that some optimization techniques requires the evaluation objective $Q(\theta)$ to be differentiable with respect to the model parameters $\theta$, but sometimes it is not the case.
Since the evaluation objective $Q(\theta)$ could not often be directly used for optimization, and we would propose a surrogate objective $\hat{Q}(\theta)$, hoping that by optimizing $\hat{Q}(\theta)$ with respect to the model parameters $\theta$, we would also achieve a good evaluation objective $Q(\theta)$. In machine learning, this surrogate objective is sometimes called training objective, and it contains the training data and the performance metric does not have to be the same to the one used in the evaluation objective. For example, the performance metric we used in machine translation model training is the sum of cross entropies, rather than BLEU score.
With the surrogate objective $\hat{Q}(\theta)$, finding the optimal parameters $\theta^{\ast}$ that maximize or minimize $\hat{Q}(\theta)$ does not happen magically. We would often need to use some optimization techniques to find the optimal parameters $\theta^{\ast}_{\hat{Q}(\theta)}$. Those optimization techniques would often introduce auxillary parameters $h$, which are often called as hyperparameters, to assist the finding of $\theta^{\ast}$. Therefore, given certain optimization techniques, the surrogate objective becomes $\hat{Q}(\theta | h)$. The hyperparameters could be some of the famous ones, such as the learning rate for gradient descent, and the regularization strength to prevent overfitting. However, this introduces some problems. The optimal parameters $\theta^{\ast}_{\hat{Q}(\theta|h)}$ for $\hat{Q}(\theta | h)$ might not be the same to the optimal parameters $\theta^{\ast}_{Q(\theta)}$ for $Q(\theta)$ which we truly care. Different $h$ would lead to different $\theta^{\ast}_{\hat{Q}(\theta|h)}$ and thus different values of $Q(\theta^{\ast}_{\hat{Q}(\theta|h)})$ which might or might not be close to $Q(\theta^{\ast}_{Q(\theta)})$.
Assuming the optimization technique would gives us good $\theta$ for $\hat{Q}(\theta | h)$, sometimes it could even be he the optimal parameters $\theta^{\ast}_{\hat{Q}(\theta|h)}$, how do we tune hyperparameters $h$ such that $Q(\theta)$ is as close to $Q(\theta^{\ast}_{Q(\theta)})$ as possible? Population based training, using the evolution of hyperparameters, is trying to solve this problem.
Population Based Training
Before we discuss the population based training, we would like to briefly review how people typically do hyperparameter tuning.
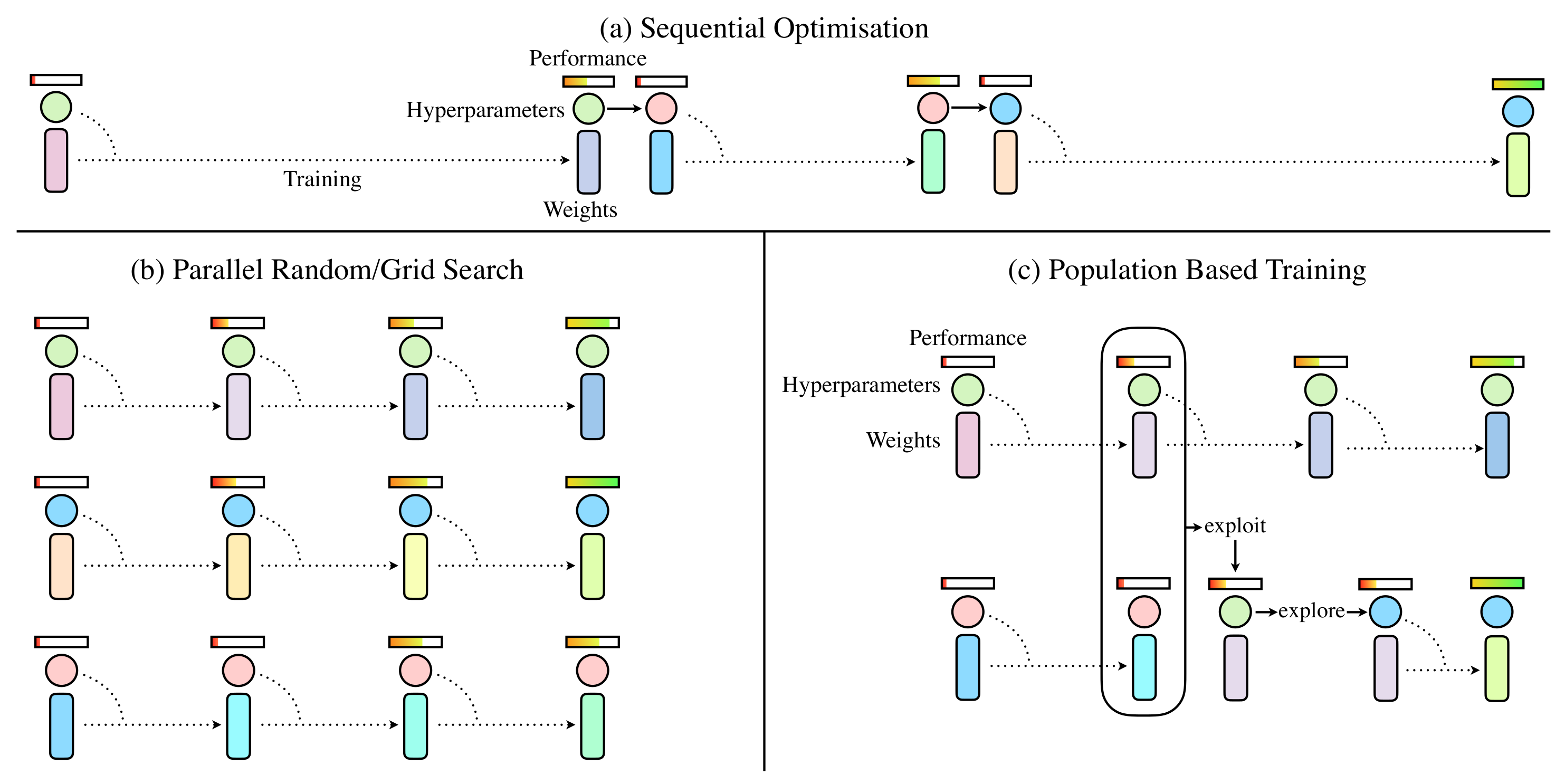
The sequential hyperparameter tuning approach is the most tedious for human beings but uses the least computation resources. We use one set of hyperparameters to train and evaluate the model. Based on the evaluation, we tune the hyperparameter and start the next round of training. We only runs one training instance throughout the entire tuning process but it could take a long time to find a good model that we feel satisfied with.
The parallel hyperparameter tuning approach is computation resource constrained. We run many training instances for different hyperparameters asynchronously, and find the best hyperparameters that gives the best evaluations. This approach, in my opinion, could hardly be called as “tuning”, since there is actually no tuning at all. The number of training instances we could run and the number of hyperparameters we would explore are solely dependent on how much computation resources we have and how much computation resource one training instance takes.
The population based hyperparameter tuning approach is a combination of the sequential approach and the parallel approach, with the human intervention in the sequential approach replaced with an automation from genetic algorithm. We run many training instance asynchronously with different hyperparameters $h_0$, and each training instance is updating the model parameters $\theta$ iteratively. At some point during the training, we compare the performances of all the training instances, and find out the one with the best performance. The rest of the training instances would start to use the exact same model parameters $\theta$ and the hyperparameters $h$ that the best training instance uses, which is called “exploitation”. Then, the hyperparameters $h$ for all the training instance other than the best training instance would be subject to some mutations, which is called “exploration”. In particular, “exploitation” means using the best configurations that the best training instance uses for all the training instances, “exploration” means mutating the hyperparameters for all the training instances other than the best training instance. The idea of population based training is simple and should be extremely familiar to the people who have experiences working with genetic algorithms.
Population Based Training Example
The DeepMind authors prepared a simple example to illustrate how the population based hyperparameter tuning approach is different from the other hyperparameter tuning approaches, such as grid search, given the same amount of computation resources.
In this particular setting, the evaluation objective is to maximize
$$
Q(\theta) = 1.2 - (\theta_0^2 + \theta_1^2)
$$
where $\theta_0$ and $\theta_1$ are model parameters. The evaluation objective is treated as a black-box which we throw in $\theta_0$ and $\theta_1$ and generates a score. The maximum evaluation score it could achieve is $1.2$ when $\theta_0 = 0$ and $\theta_0 = 1$.
The surrogate objective we proposed is to maximize
$$
\hat{Q}(\theta | h) = 1.2 - (h_0 \theta_0^2 + h_1 \theta_1^2)
$$
where $h_0$ and $h_1$ are hyperparameters. We would use gradient ascent iteratively, with a fixed learning rate $\eta$, to optimize this surrogate objective, given the hyperparameters $h_0$ and $h_1$ and initial parameters $\theta_0$ and $\theta_1$.
Lucky us, the surrogate objective is very close to the black-box evaluation objective. If somehow we could be more lucky and use hyperparameters $h_0=1$ and $h_1=1$, optimizing surrogate objective would be equivalent to optimizing the evaluation objective, and we would be the most likely to have the maximum evaluation score.
We were given computation resources that allows running two training instances simultaneously. This time, we are not extremely lucky again. We used $\{h_0=1, h_1=0\}$ and $\{h_0=0, h_1=1\}$ as the initial hyperparameters for the two training instances, respectively. We want to check which hyperparameter tuning approach results in the best evaluation score, given the same amount of computation resources.
To make it “fair”, the model should be initialized with parameters $\theta_0=0.9$ and $\theta_1=0.9$, and each training instance is only allowed to use gradient ascent to update the hyperparameter $40$ times. The author did not mention what learning rate $\eta$ to use, but is the same for all training instances in all hyperparameter tuning approaches.
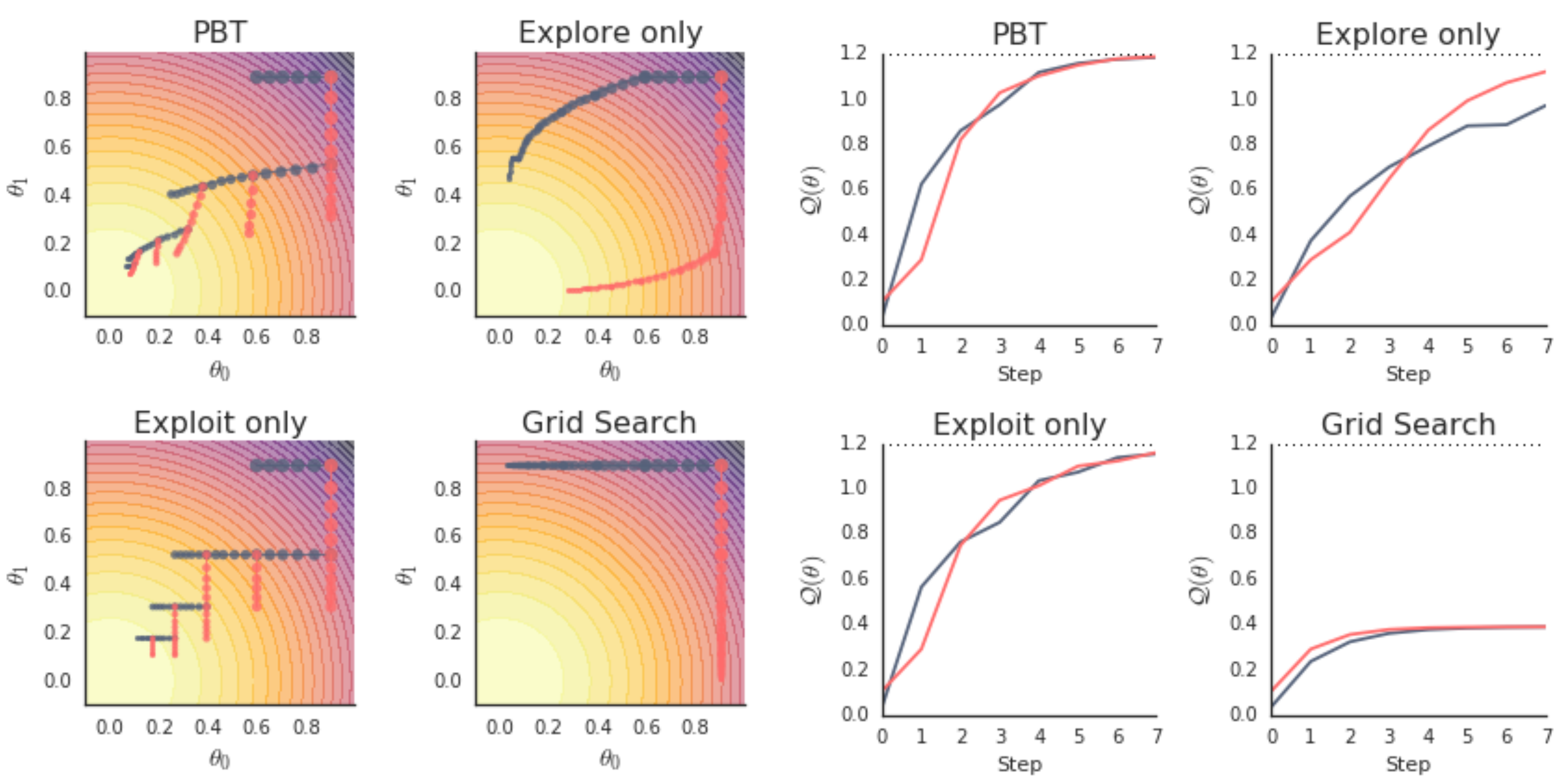
The DeepMind authors created contour plots to make it easy to understand. The lighter the region is in the plot, the higher the evaluation score is. One training instance is denoted using black nodes, where each node represents the model parameters for each update iteration. The other training instance is denoted using red nodes. There are $2 \times 40 = 80$ nodes in total in one contour plot.
For grid search, because there is no actual hyperparameter tuning during training, $h_0$ and $h_1$ remain the same for the two training instances and the evaluation score is much lower than the possible maximum value $1.2$. In fact, it could never reach or get close to $1.2$ no matter how many gradient ascent iterations it does. This is a typical example of insufficient computation resource for grid search results in models with bad performance.
The population based training is scheduled to do exploration and exploitation every $5$ gradient ascent iterations. Surprisingly or not, it gets close to the possible maximum value $1.2$ in the $40$ gradient ascent iterations. Removing exploration or exploitation from the population based training has also been investigated. The model trained from neither of the two is as good as the one trained from the intact population based training in $40$ iterations of gradient ascent.
It should be noted that the exploration the author used is not purely random. Otherwise, the exploration might results in negative values for hyperparameters $h_0$ and $h_1$ and cause the optimization deviate from the maximum evaluation score.
FAQs
What is Hyperparameter Tuning?
Some models could be trained better with dynamically changed hyperparameters, rather than fixed hyperparameters throughout the training process. Learning rate decay used for neural network optimization is one of the typical examples.
Can We Reproduce the Best Model from the Population Based Training Using the Best Final Hyperparameters?
No. To reproduce the training of the best model parameters, we would need know how its hyperparameter tuning trajectory throughout the population based training.
Do We Care About Hyperparameters After Population Based Training?
No. The model itself does not have hyperparameters $h$. It only has parameters $\theta$. Therefore, we could only save a copy of the model parameters $\theta$ and ignore the hyperparameters $h$ when the population based training is finished.
What Optimization Methods Could Be Used for Population Based Training?
In theory, we could use any iterative optimization methods, such as gradient descent, for population based training. DeepMind has shown that population based training works very well for neural network optimizations using gradient descent. There is no evidence shown that population based training would work for other iterative optimization methods. However, it does not prevent you from using the iterative optimization methods you are interested in with the population based training.
Final Remarks
I remember when I was in college and neural networks and gradient descent have not been proved useful for solving practical problems, we used genetic algorithms for optimizing models and the models do not have to be differentiable. While DeepMind did not invent genetic algorithms and the idea of the population based training is almost the exactly the same to a conventional genetic algorithm, it is the first optimization method that combines genetic algorithm and one other optimization algorithm, which could be gradient descent, to solve neural network optimization problems in practice.
Distributed application library Ray has a sub-library, Tune, for distributed population based training. This might make the optimization easier from a programmer’s perspective.
References
Population Based Training