Quantum Bit and Bloch Sphere
Introduction
A quantum bit or a qubit is a unit of information describing a two-dimensional quantum system. It is also a key basic unit to the quantum computer. Usually it could be visualized using a Bloch sphere.
In this blog post, I would like to derive the connections between qubit and Bloch sphere.
Classical Bit
A classical bit is a unit of information describing a two-dimensional classical system. A classical bit could only be in one state, either $| 0 \rangle$ or $| 1 \rangle$. $| 0 \rangle$ and $| 1 \rangle$ are orthogonal basis. Usually $| 0 \rangle = [1, 0]^{\top}$ and $| 1 \rangle = [0, 1]^{\top}$.
Quantum Bit (Qubit)
A quantum bit or a qubit is a unit of information describing a two-dimensional quantum system. A qubit is a superposition of two basic states, $| 0 \rangle$ and $| 1 \rangle$.
A generic (normalized) qubit is of the form
$$
\begin{align}
| \psi \rangle &= c_0 | 0 \rangle + c_1 | 1 \rangle \\
\end{align}
$$
where $c_0$ and $c_1$ are complex numbers, and $|c_0|^2 + |c_1|^2 = 1$. After taking the measurement for $| \psi \rangle$, the system would be collapsed to $| 0 \rangle$ with probability $|c_0|^2$ or $| 1 \rangle$ with probability $|c_1|^2$.
A complex number could be described using exponential form.
$$
c_0 = \rho_0 e^{i\theta_0} = \rho_0 (\cos \theta_0 + i \sin \theta_0) \\
c_1 = \rho_1 e^{i\theta_1} = \rho_1 (\cos \theta_1 + i \sin \theta_1) \\
$$
Where $\rho_0$ and $\rho_1$ are real numbers. Therefore,
$$
\begin{align}
|c_0|^2 + |c_1|^2 &= |\rho_0 e^{i\theta_0}|^2 + |\rho_1 e^{i\theta_1}|^2 \\
&= |\rho_0|^2 |e^{i\theta_0}|^2 + |\rho_1|^2 |e^{i\theta_1}|^2 \\
&= |\rho_0|^2 |\cos \theta_0 + i \sin \theta_0|^2 + |\rho_1|^2 |\cos \theta_1 + i \sin \theta_1|^2 \\
&= |\rho_0|^2 + |\rho_1|^2 \\
&= 1 \\
\end{align}
$$
We could rewrite $\rho_0$ and $\rho_1$ using a new parameter $\frac{\theta}{2}$. We would see why we used $\frac{\theta}{2}$ instead of $\theta$ shortly.
$$
\rho_0 = \cos \frac{\theta}{2} \\
\rho_1 = \sin \frac{\theta}{2} \\
$$
We multiple a complex number $e^{-i\theta_0}$ to $| \psi \rangle$.
$$
\begin{align}
e^{-i\theta_0} | \psi \rangle &= e^{-i\theta_0} c_0 | 0 \rangle + e^{-i\theta_0} c_1 | 1 \rangle \\
&= e^{-i\theta_0} \rho_0 e^{i\theta_0} | 0 \rangle + e^{-i\theta_0} \rho_1 e^{i\theta_1} | 1 \rangle \\
&= \rho_0 | 0 \rangle + \rho_1 e^{i(\theta_1 - \theta_0)} | 1 \rangle \\
&= \cos \frac{\theta}{2} | 0 \rangle + e^{i(\theta_1 - \theta_0)} \sin \frac{\theta}{2} | 1 \rangle \\
\end{align}
$$
We define $\varphi = \theta_1 - \theta_0$, we have
$$
\begin{align}
e^{-i\theta_0} | \psi \rangle &= \cos \frac{\theta}{2} | 0 \rangle + e^{i\varphi} \sin \frac{\theta}{2} | 1 \rangle \\
\end{align}
$$
As we have discussed early in quantum system states, quantum system state $| \psi \rangle$ and $c | \psi \rangle$, where $c$ is any non-zero complex number, represent the same quantum system state. Since $e^{-i\theta_0}$ is a non-zero complex number, $| \psi \rangle$ and $e^{-i\theta_0} | \psi \rangle$ represent the same quantum system state. So we have
$$
\begin{align}
| \psi \rangle &= \cos \frac{\theta}{2} | 0 \rangle + e^{i\varphi} \sin \frac{\theta}{2} | 1 \rangle \\
\end{align}
$$
This means that, with two parameters $\theta$ and $\varphi$, we could determine a qubit state.
The next question is what is the minimum range of $\theta$ and $\varphi$ so that all the possible qubit states, $| \psi \rangle \in \mathbb{C}^2$s, are included? After taking the measurement of the qubit, the probability of observing $| 0 \rangle$ is $\cos^2 \frac{\theta}{2}$ and the probability of observing $| 1 \rangle$ is $\sin^2 \frac{\theta}{2}$. For different $\theta$s, if $\cos^2 \frac{\theta}{2}$s are the same, the qubit states, $| \psi \rangle$s, are also the same. Apparently, $0 \leq \frac{\theta}{2} \leq \frac{\pi}{2}$, i.e., $0 \leq \theta \leq \pi$. If $\theta$ is out of this range, there is always a way to convert the $\theta$ into the range of $[0, \pi]$ while keeping $\cos^2 \frac{\theta}{2}$ the same. For $\varphi$, there is not too much to say, $0 \leq \varphi < 2\pi$.
To summarize, a qubit could be described using two independent variables.
$$
\begin{align}
| \psi \rangle &= \cos \frac{\theta}{2} | 0 \rangle + e^{i\varphi} \sin \frac{\theta}{2} | 1 \rangle \\
\end{align}
$$
Where $\theta \in [0, \pi]$ and $\varphi \in [0, 2\pi)$.
Bloch Sphere
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
Given the two-variable qubit formulation we derived above, it could perfectly fit into the Bloch sphere.
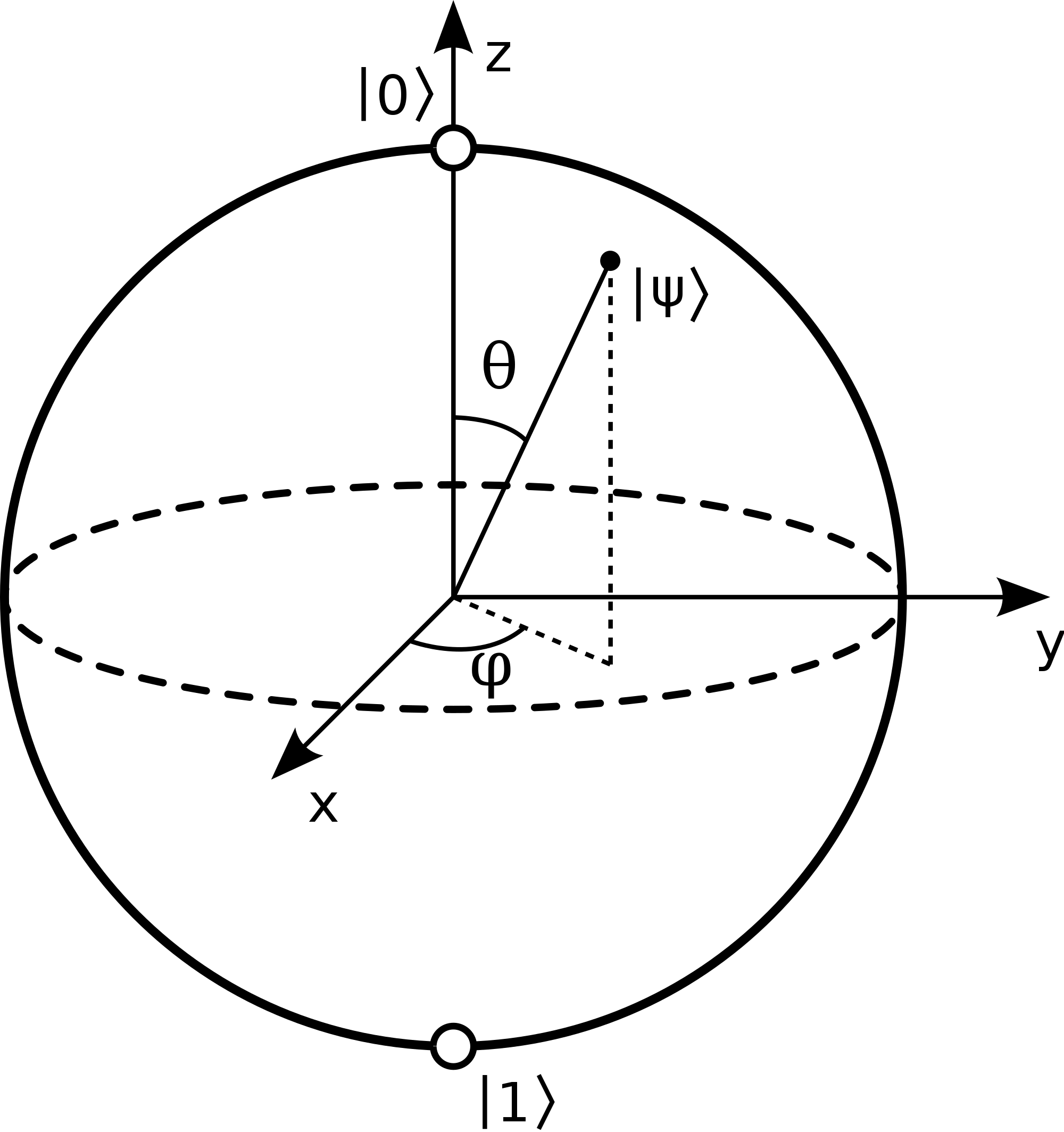
The north and south poles of the Bloch sphere are typically chosen to correspond to the standard basis vectors $ |0\rangle $ and $ |1\rangle $, respectively. Any coordinate, which could be uniquely described using $\theta$ and $\varphi$, on the sphere, represents a unique qubit.
It is also non-trivial to see that all the qubits on the equator, where $\theta = \frac{\pi}{2}$, have equal probability of collapsing to $ |0\rangle $ and $ |1\rangle $, because $p(|0\rangle) = \cos^2 \frac{\pi}{4} = \frac{1}{2}$ and $p(|1\rangle) = \sin^2 \frac{\pi}{4} = \frac{1}{2}$.
In addition, if the qubit is more closer to the north pole, there is larger chance to collapse to $ |0\rangle $ after taking the measurement. Similarly, if the qubit is more closer to the south pole, there is larger chance to collapse to $ |1\rangle $ after taking the measurement.
Moreover, an arbitrary pair of orthogonal qubits is mapped to antipodal (opposite) points of the Bloch sphere. This is because, any antipodal qubits have the following representations.
$$
\begin{align}
| \psi \rangle &= \cos \frac{\theta}{2} | 0 \rangle + e^{i\varphi} \sin \frac{\theta}{2} | 1 \rangle \\
| \psi^{\prime} \rangle &= \cos \frac{\pi - \theta}{2} | 0 \rangle + e^{i(\varphi + \pi)} \sin \frac{\pi - \theta}{2} | 1 \rangle \\
\end{align}
$$
We would like to show that $\langle \psi , \psi^{\prime} \rangle = 0$ so that $| \psi \rangle $ and $| \psi^{\prime} \rangle$ are orthogonal.
Proof
$$
\begin{align}
\langle \psi , \psi^{\prime} \rangle &= \langle \cos \frac{\theta}{2} | 0 \rangle + e^{i\varphi} \sin \frac{\theta}{2} | 1 \rangle, \cos \frac{\pi - \theta}{2} | 0 \rangle + e^{i(\varphi + \pi)} \sin \frac{\pi - \theta}{2} | 1 \rangle \rangle \\
&= \cos \frac{\theta}{2} \overline{\cos \frac{\pi - \theta}{2}} \langle | 0 \rangle, | 0 \rangle \rangle + \cos \frac{\theta}{2} \overline{e^{i(\varphi + \pi)} \sin \frac{\pi - \theta}{2}} \langle | 0 \rangle, | 1 \rangle \rangle \\
&\qquad + e^{i\varphi} \sin \frac{\theta}{2} \overline{\cos \frac{\pi - \theta}{2}} \langle | 1 \rangle, | 0 \rangle \rangle + e^{i\varphi} \sin \frac{\theta}{2} \overline{e^{i(\varphi + \pi)} \sin \frac{\pi - \theta}{2}} \langle | 1 \rangle, | 1 \rangle \rangle \\
&= \cos \frac{\theta}{2} \overline{\cos \frac{\pi - \theta}{2}} + e^{i\varphi} \sin \frac{\theta}{2} \overline{e^{i(\varphi + \pi)} \sin \frac{\pi - \theta}{2}} \\
&= \cos \frac{\theta}{2} \cos \frac{\pi - \theta}{2} + e^{i\varphi} \sin \frac{\theta}{2} \overline{e^{i(\varphi + \pi)}} \overline{\sin \frac{\pi - \theta}{2}} \\
&= \cos \frac{\theta}{2} \cos \frac{\pi - \theta}{2} + e^{i\varphi} \sin \frac{\theta}{2} e^{i(-\varphi - \pi)} \sin \frac{\pi - \theta}{2} \\
&= \cos \frac{\theta}{2} \cos \frac{\pi - \theta}{2} + e^{i(-\pi)} \sin \frac{\theta}{2} \sin \frac{\pi - \theta}{2} \\
&= \cos \frac{\theta}{2} \cos \frac{\pi - \theta}{2} + \sin \frac{\theta}{2} \sin \frac{\pi - \theta}{2} \\
&= \cos (\frac{\theta}{2} + \frac{\pi - \theta}{2}) \\
&= \cos \frac{\pi}{2} \\
&= 0 \\
\end{align}
$$
This concludes the proof.
Last but not least, to answer why we had used $\frac{\theta}{2}$ instead of $\theta$ in the qubit representation, it is because we want to make the qubit representation compatible with the Bloch sphere. If using $\frac{\theta}{2}$, $\theta \in [0, \pi]$ in the Bloch sphere matches $\theta \in [0, \pi]$ in the qubit representation.
Manipulate Qubit on Bloch Sphere
As we have partially shown in one of my previous posts, all the classical logical gates could be considered as matrices, and all the classical bit manipulations are matrix multiplications. This also applies to quantum logical gates and qubits. Actually, all the quantum logical gates are unitary matrices. We would take this fact for now and I would probably explain this in my future blog posts.
Matrix $U$ is unitary if and only if
$$
U^{\dagger}U = UU^{\dagger} = I
$$
Unitary matrix preserves inner products. If $U$ is unitary, then for any $v, v^{\prime} \in \mathbb{C}^{n}$, we have $\langle Uv, Uv^{\prime} \rangle = \langle v, v^{\prime} \rangle$.
This could be easily proved by using the inner product properties.
$$
\begin{align}
\langle Uv, Uv^{\prime} \rangle &= (Uv^{\prime})^{\dagger} (Uv) \\
&= v^{\prime\dagger} U^{\dagger} Uv \\
&= v^{\prime\dagger} (U^{\dagger} U) v \\
&= v^{\prime\dagger} I v \\
&= v^{\prime\dagger} v \\
&= \langle v, v^{\prime} \rangle \\
\end{align}
$$
This means that unitary matrix $U$ also preserves the norm of any vector $v \in \mathbb{C}^{n}$.
$$
\begin{align}
|Uv|^2 &= \langle Uv, Uv \rangle \\
&= \langle v, v \rangle \\
&= |v|^2 \\
\end{align}
$$
Suppose we have a qubit $| \psi \rangle$ and unitary matrix $U$. Because $| \psi | = 1$, so $| U\psi | = 1$. In addition, given the orthogonal basis $|0\rangle$ and $|1\rangle$, because $\langle |0\rangle, |1\rangle \rangle = 1$, so $ \langle U|0\rangle, U |1\rangle \rangle = 1$. This means that $U|0\rangle$ and $U|1\rangle$ are a new pair of orthogonal basis.
On the Bloch sphere, applying a unitary matrix $U$ to qubit $| \psi \rangle$ is equivalent to moving the coordinate of the qubit on the Block sphere, since unitary matrix preserves the norm of vector. Apply a unitary matrix $U$ to both $|0\rangle$ and $|1\rangle$ is equivalent to rotate the north and south poles, i.e. the coordinate system, accordingly.
If we look into $| U \psi \rangle$ more closely.
$$
\begin{align}
| U \psi \rangle &= U \Big( \cos \frac{\theta}{2} | 0 \rangle + e^{i\varphi} \sin \frac{\theta}{2} | 1 \rangle \Big) \\
&= \cos \frac{\theta}{2} (U | 0 \rangle) + e^{i\varphi} \sin \frac{\theta}{2} (U | 1 \rangle) \\
\end{align}
$$
Since $U|0\rangle$ and $U|1\rangle$ are also orthogonal basis, manipulating qubit is also equivalent to manipulating the entire coordinate system. The coordinates of $| U \psi \rangle$ in the new coordinate system ($U|0\rangle$, $U|1\rangle$) is the same to the coordinates of $| \psi \rangle$ in the old coordinate system ($|0\rangle$, $|1\rangle$).
Bit VS Qubit
For a classic system consisting of $n$ binary components, there are $2^n$ different system states possible in total. Representing a classic system state only requires computer memory consisting of $n$ bits. Quantum system state consisting of $n$ binary components, however, is a superposition of all the $2^n$ different system states possible. The complex-numbered coefficients for all the possible system states are used to describe the quantum system state. Therefore, if simulating a quantum system state on a classic computer, the memory requirement will be $2^n \times \text{sizeof}(\text{complex number})$, i.e., $O(2^n)$, bits. This means, without some kind of approximation or special constraints or setups, simulating quantum system state on a classic computer is not feasible. For example, suppose the classic computer has $1$TB, which is equivalent to $2^{10} \times 2^{10} \times 2^{10} \times 2^{10} \times 2^3 = 2^{43}$ bits, of memory, and $\text{sizeof}(\text{complex number}) = 2^6$ bits which is just two $32$-bit floating point values, we could only represent quantum system consisting of at most $43 - 6 = 37$ qubits, not to mention doing other mathematical operations.
References
Quantum Bit and Bloch Sphere