Reparameterization Trick
Introduction
In directed probabilistic graphical models where neural networks are used to encode latent variables, the model optimization would often encounter the problem that the sampling function is not differentiable with respect to the parameters that are used for generating the latent variable samples.
Reparameterization trick is a technique that is used to make the sampling function differentiable with respect to the parameters that are used for generating the samples. In this article, we will present and what the reparameterization trick is and how it is used in practice.
Directed Probabilistic Graphical Models
Model Definition
Directed probabilistic graphical models, also known as Bayesian networks, are a type of probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph (DAG). The nodes of the graph represent random variables, and the edges represent conditional dependencies between the random variables. The graph encodes a factorization of the joint probability distribution of the random variables.
$$
p_{\boldsymbol{\theta}}(\mathbf{x}_{1}, \cdots, \mathbf{x}_{N}) = \prod_{i=1}^{N} p_{\boldsymbol{\theta}}(\mathbf{x}_{i} | \text{Pa}(\mathbf{x}_{i}))
$$
where $\text{Pa}(\mathbf{x}_{i})$ denotes the parents of $\mathbf{x}_{i}$ in the graph.
Learning Model Parameters
Learning a good directed probabilistic graphical model is useful for understanding the underlying structure of the data and creating synthetic that follows the distribution of the true data.
Learning the parameters of a directed probabilistic graphical model, $\boldsymbol{\theta}$, usually requires computing the estimation of some random variables over a posterior distribution of a latent variable. There are usually two ways to compute the estimation. One is to derive the closed-form solution and the other is to use the Monte Carlo method to estimate by sampling from the posterior distribution.
The former one is sometimes infeasible because of the difficulty in deriving the closed-form solution. The latter one, while inefficient, is usually feasible and is used in practice.
Differentiation Problem
However, when sampling is used to estimate the posterior distribution and gradient descent is used for updating the parameters, if the sampling function is not differentiable, then the gradient of the estimation with respect to the parameters that are used for generating the samples cannot be computed. Therefore, we have to come up with a differentiable sampling function so that the parameters can be updated by gradient descent. This is where the reparameterization trick comes in.
Reparameterization Trick
The reparameterization trick, while sounds confusing, fundamentally is just a way to transform a random variable in a deterministic way so that the transformed random variable follows a desired distribution. In this way, the sampling function becomes differentiable with respect to the parameters that are used for generating the samples.
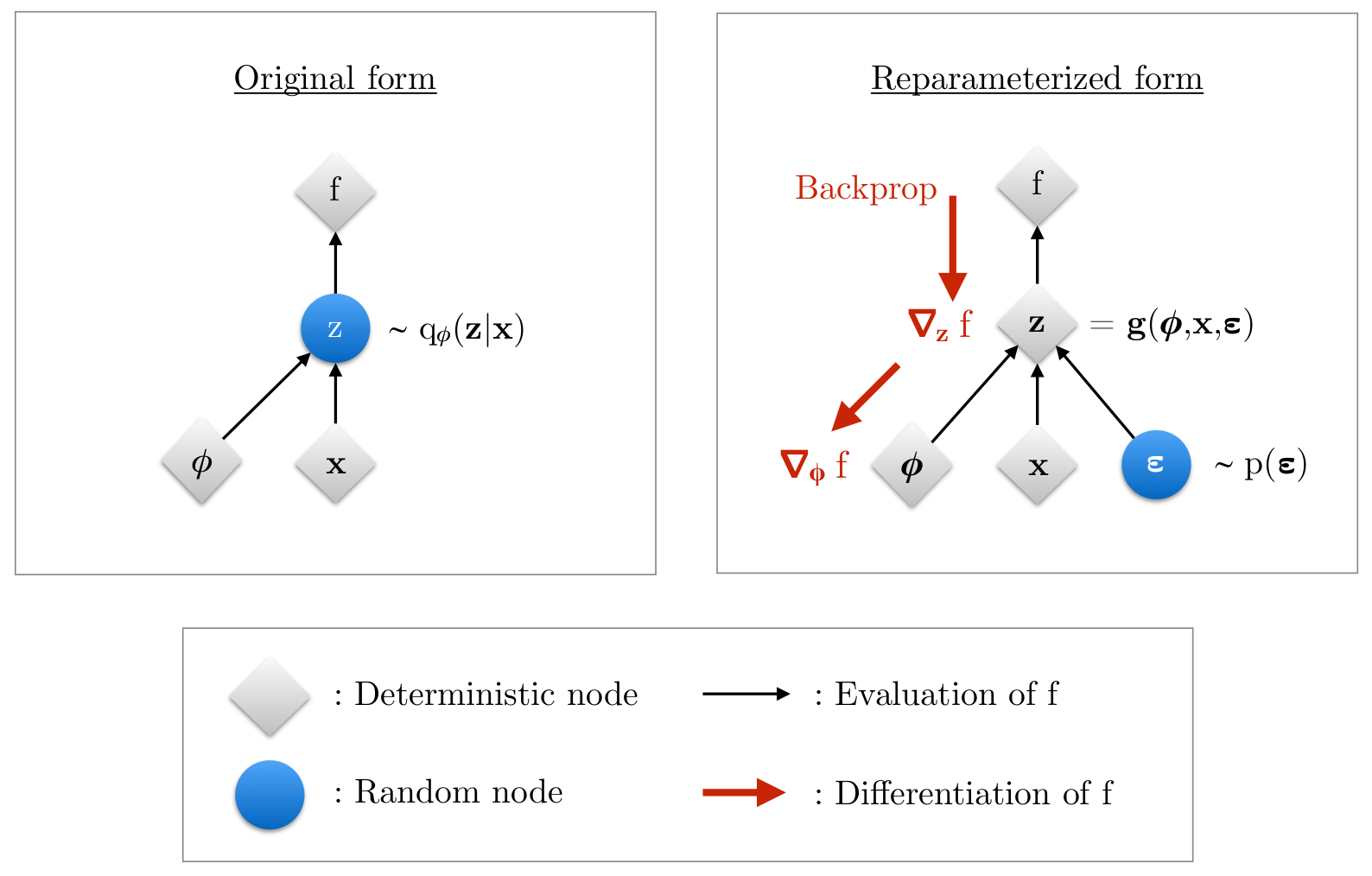
Now the question is, how to construct a variable transformation such that the transformed random variable follows a desired distribution?
According to the transformations of variables that we have proved in the previous article “Transformations of Random Variables”, the probability density function between the original random variable and the transformed random variable is only scaled by a scalar which is the absolute value of the determinant of the Jacobian matrix of the inverse transformation. Therefore, the distributions of the original random variable and the transformed random variable must belong to the same family. For continuous distributions, the rule of the probability density function of the transformed random variable can be described as follows.
Suppose that $\mathbf{X}$ is a random variable taking values in $S \subseteq \mathbb{R}^n$, and $X$ has a continuous distribution with probability density function $f$. In addition, suppose $\mathbf{Y} = r(\mathbf{X})$, where $r: S \to T$, $T \subseteq \mathbb{R}^m$, and $r$ is a one-to-one transformation. Then $\mathbf{Y}$ has a continuous distribution with probability density function $g$ given by
$$
\begin{align}
g(\mathbf{y})
&= f(r^{-1}(\mathbf{y})) \left| \det \mathbf{J}_{r^{-1}}(\mathbf{y}) \right| \\
&= f(\mathbf{x}) \left| \det \mathbf{J}_{r^{-1}}(\mathbf{y}) \right| \\
&= \frac{f(\mathbf{x})}{\left| \det \mathbf{J}_r(\mathbf{x}) \right|}
\end{align}
$$
where $\mathbf{y} = r(\mathbf{x})$, $\mathbf{x} = r^{-1}(\mathbf{y})$, $\mathbf{J}_r(\mathbf{x})$ is the Jacobian matrix of $r$ at $\mathbf{x}$, and $\mathbf{J}_{r^{-1}}(\mathbf{y})$ is the Jacobian matrix of $r^{-1}$ at $\mathbf{y}$.
Example
Univariate Normal Distribution
If the random variable $X$ should follow a desired normal distribution $\mathcal{N}(\mu, \sigma^2)$ in which $\mu$ and $\sigma^2$ are also random variables. The probability density function $P(X = x)$ is given by
$$
P(X = x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)
$$
We want to construct a transformation $r$ such that $X = r(Z)$ and $Z$ must also follow a normal distribution. Because $\mu$ and $\sigma^2$ are also random variables, the normal distribution that $Z$ follows must not be a function of $\mu$ and $\sigma^2$. Otherwise, we still have the same problem that the sampling function is not differentiable with respect to $\mu$ and $\sigma^2$. Thus, we can just pick a standard normal distribution $\mathcal{N}(0, 1)$ for $Z$. The probability density function $P(Z = z)$ is given by
$$
P(Z = z) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right)
$$
Now we need to construct a transformation $r$ such that $X = r(Z)$ in which $X$ follows a normal distribution $\mathcal{N}(\mu, \sigma^2)$ and $Z$ follows a standard normal distribution $\mathcal{N}(0, 1)$.
Because
$$
\begin{align}
P(X = x)
&= P(X = r(z)) \\
&= P(Z = r^{-1}(x)) \left| \det \mathbf{J}_{r^{-1}}(x) \right| \\
&= P(Z = z) \left| \det \mathbf{J}_{r^{-1}}(x) \right| \\
&= \frac{P(Z = z)}{\left| \det \mathbf{J}_r(z) \right|}
\end{align}
$$
We can plug in the probability density functions of $X$ and $Z$ to get
$$
\begin{align}
P(X = x)
&= P(X = r(z)) \\
&= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(r(z) - \mu)^2}{2\sigma^2}\right) \\
&= \frac{P(Z = z)}{\left| \det \mathbf{J}_r(z) \right|} \\
&= \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right) \cdot \frac{1}{\left| \det \mathbf{J}_r(z) \right|}
\end{align}
$$
From this relation, we can see that $r(z) = \mu + \sigma z$ and $\left| \det \mathbf{J}_r(z) \right| = \sigma$. It turns out that the absolute value of the determinant of the Jacobian matrix of the transformation $\left| \det \mathbf{J}_r(z) \right|$ is also consistent with what we could calculate from $r(z) = \mu + \sigma z$, confirming this transformation is correct.
Therefore, the transformation from $Z$ to $X$ is given by
$$
X = \mu + \sigma Z
$$
Multivariate Normal Distribution
If the $k$-dimensional random variable $\mathbf{X} \in \mathbb{R}^k$, represented using a column vector, should follow a desired multivariate normal distribution $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$ in which $\boldsymbol{\mu}$ and $\boldsymbol{\Sigma}$ are also random variables. The probability density function $P(\mathbf{X} = \mathbf{x})$ is given by
$$
P(\mathbf{X} = \mathbf{x}) = \frac{1}{(2\pi)^{\frac{k}{2}} \left( \det \boldsymbol{\Sigma} \right)^{\frac{1}{2}}} \exp\left(-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^{\top} \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)
$$
We want to construct a transformation $r$ such that $\mathbf{X} = r(\mathbf{Z})$ and $\mathbf{Z}$ must also follow a multivariate normal distribution. Because $\boldsymbol{\mu}$ and $\boldsymbol{\Sigma}$ are also random variables, the multivariate normal distribution that $\mathbf{Z}$ follows must not be a function of $\boldsymbol{\mu}$ and $\boldsymbol{\Sigma}$. Otherwise, we still have the same problem that the sampling function is not differentiable with respect to $\boldsymbol{\mu}$ and $\boldsymbol{\Sigma}$. Thus, we can just pick a standard multivariate normal distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$ for $\mathbf{Z}$. The probability density function $P(\mathbf{Z} = \mathbf{z})$ is given by
$$
P(\mathbf{Z} = \mathbf{z}) = \frac{1}{(2\pi)^{\frac{k}{2}}} \exp\left(-\frac{1}{2} \mathbf{z}^{\top} \mathbf{z}\right)
$$
Now we need to construct a transformation $r$ such that $\mathbf{X} = r(\mathbf{Z})$ in which $\mathbf{X}$ follows a multivariate normal distribution $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$ and $\mathbf{Z}$ follows a standard multivariate normal distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$.
Because
$$
\begin{align}
P(\mathbf{X} = \mathbf{x})
&= P(\mathbf{X} = r(\mathbf{z})) \\
&= P(\mathbf{Z} = r^{-1}(\mathbf{x})) \left| \det \mathbf{J}_{r^{-1}}(\mathbf{x}) \right| \\
&= P(\mathbf{Z} = \mathbf{z}) \left| \det \mathbf{J}_{r^{-1}}(\mathbf{x}) \right| \\
&= \frac{P(\mathbf{Z} = \mathbf{z})}{\left| \det \mathbf{J}_r(\mathbf{z}) \right|}
\end{align}
$$
We can plug in the probability density functions of $\mathbf{X}$ and $\mathbf{Z}$ to get
$$
\begin{align}
P(\mathbf{X} = \mathbf{x})
&= P(\mathbf{X} = r(\mathbf{z})) \\
&= \frac{1}{(2\pi)^{\frac{k}{2}} \left( \det \boldsymbol{\Sigma} \right)^{\frac{1}{2}}} \exp\left(-\frac{1}{2} (r(\mathbf{z}) - \boldsymbol{\mu})^{\top} \boldsymbol{\Sigma}^{-1} (r(\mathbf{z}) - \boldsymbol{\mu})\right) \\
&= \frac{P(\mathbf{Z} = \mathbf{z})}{\left| \det \mathbf{J}_r(\mathbf{z}) \right|} \\
&= \frac{1}{(2\pi)^{\frac{k}{2}}} \exp\left(-\frac{1}{2} \mathbf{z}^{\top} \mathbf{z}\right) \cdot \frac{1}{\left| \det \mathbf{J}_r(\mathbf{z}) \right|}
\end{align}
$$
From this relation, we can see that $\mathbf{r}(\mathbf{z}) = \boldsymbol{\mu} + \boldsymbol{A} \mathbf{z}$, where $\boldsymbol{A}$ is a matrix such that $\boldsymbol{A}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{A} = \boldsymbol{I}$, and $\left| \det \mathbf{J}_r(\mathbf{z}) \right| = \left( \det \boldsymbol{\Sigma} \right)^{\frac{1}{2}}$.
Because
$$
\begin{align}
\boldsymbol{\Sigma}^{-1}
&= \left(\boldsymbol{A}^{\top} \right)^{-1} \boldsymbol{A}^{-1} \\
&= \left( \boldsymbol{A} \boldsymbol{A}^{\top} \right)^{-1} \\
\end{align}
$$
We must have $\boldsymbol{\Sigma} = \boldsymbol{A} \boldsymbol{A}^{\top}$.
To derive the matrix $\boldsymbol{A}$, we can perform the Cholesky decomposition for $\boldsymbol{\Sigma}$ and the matrix $\boldsymbol{A}$ turns out to be a lower triangular matrix $\boldsymbol{L}$ such that $\boldsymbol{\Sigma} = \boldsymbol{L} \boldsymbol{L}^{\top}$. Based on the multiplicativity property of the determinant, we have $\left| \det \boldsymbol{\Sigma} \right| = \left| \det \boldsymbol{L} \right| \left| \det \boldsymbol{L}^{\top} \right| = \left| \det \boldsymbol{L} \right|^2$. Therefore, $\left| \det \boldsymbol{\Sigma} \right|^{\frac{1}{2}} = \left| \det \boldsymbol{L} \right|$. In addition, the determinant of a lower triangular matrix is the product of the diagonal elements. Therefore, $\left| \det \boldsymbol{L} \right| = \prod_{i=1}^{k} L_{ii}$.
References
Reparameterization Trick