Simon's Algorithm
Introduction
Simon’s algorithm is a quantum computing algorithm invented to solve a contrived problem which is called Simon’s problem. Compared to one of the other quantum computing algorithms, Deutsch-Jozsa algorithm, which only requires to run once, Simon’s algorithm requires to run the algorithm multiple times, yet it is still able to solve Simon’s problem exponentially faster asymptotically running on quantum circuits than the best conventional probabilistic algorithm running on classical circuits.
In this blog post, I would like to discuss Simon’s problem in details.
Prerequisites
XOR Properties
- Commutativity: $A \oplus B = B \oplus A$
- Associativity: $A \oplus (B \oplus C) = (A \oplus B) \oplus C$
- Identity element: $A \oplus 0 = A$
- Self-invertible: $A \oplus A = 0$
Reducing Sum or Difference to Boolean
If $x$ and $y$ are binary values, $x, y \in \{0, 1\}$, we have
$$
\begin{align}
(-1)^{x + y} &= (-1)^{x \oplus y} \\
(-1)^{x - y} &= (-1)^{x \oplus y} \\
\end{align}
$$
where $\oplus$ is $\text{XOR}$ (binary addition modulo 2). This could be easily verified using truth table.
Inner Product and Inner Product Space for Binary Vector Space
In the previous blog post, we have defined the inner product and inner product space for complex vector space. Similarly, we could also define the inner product and inner product space for binary vector space.
$$
\begin{align}
\langle -, - \rangle : \{0,1\}^n \times \{0,1\}^n \rightarrow \{0,1\}
\end{align}
$$
Given two binary vectors $\mathbf{x}, \mathbf{y} \in \{0,1\}^n$, $\mathbf{x} = \{x_0, x_1, \cdots, x_{n-1}\}$ and $\mathbf{y} = \{y_0, y_1, \cdots, y_{n-1}\}$, the inner product of $\mathbf{x}$ and $\mathbf{y}$ is defined as
$$
\begin{align}
& \langle \mathbf{x}, \mathbf{y} \rangle \\
&= (x_0 \wedge y_0) \oplus (x_1 \wedge y_1) \oplus \cdots \oplus (x_{n-1} \wedge y_{n-1}) \\
&= \bigoplus_{i=0}^{n-1} (x_i \wedge y_i ) \\
\end{align}
$$
which is somewhat similar to the inner product definition for real vector space.
The bitwise exclusive-or operation $\oplus$ was also defined for binary vectors $\mathbf{x}$ and $\mathbf{y}$ of the same length. Given two binary vectors $\mathbf{x}, \mathbf{y} \in \{0,1\}^n$, $\mathbf{x} = \{x_0, x_1, \cdots, x_{n-1}\}$ and $\mathbf{y} = \{y_0, y_1, \cdots, y_{n-1}\}$,
$$
\begin{align}
\mathbf{x} \oplus \mathbf{y} = \{x_0 \oplus y_0, x_1 \oplus y_1, \cdots, x_{n-1} \oplus y_{n-1}\}
\end{align}
$$
The following inner product properties are satisfied based on the above inner product definition.
Given $\mathbf{x}, \mathbf{x}^{\prime}, \mathbf{y}, \mathbf{y}^{\prime} \in \{0,1\}^n$, using the $\text{XOR}$ distributivity property we derived above,
$$
\begin{align}
& \langle \mathbf{x} \oplus \mathbf{x}^{\prime}, \mathbf{y} \rangle \\
&= \big((x_0 \oplus x_0^{\prime})\wedge y_0\big) \oplus \big((x_1 \oplus x_1^{\prime}) \wedge y_1\big) \oplus \cdots \\
&\qquad \oplus \big((x_{n-1} \oplus x_{n-1}^{\prime}) \wedge y_{n-1}\big) \\
&= \big((x_0 \wedge y_0) \oplus (x_0^{\prime} \wedge y_0) \big) \oplus \big((x_1 \wedge y_1) \oplus (x_1^{\prime} \wedge y_1) \big) \oplus \cdots \\
&\qquad \oplus \big((x_{n-1} \wedge y_{n-1}) \oplus (x_{n-1}^{\prime} \wedge y_{n-1}) \big) \\
&= (x_0 \wedge y_0) \oplus (x_0^{\prime} \wedge y_0) \oplus (x_1 \wedge y_1) \oplus (x_1^{\prime} \wedge y_1) \oplus \cdots \\
&\qquad \oplus (x_{n-1} \wedge y_{n-1}) \oplus (x_{n-1}^{\prime} \wedge y_{n-1}) \\
&= \big( (x_0 \wedge y_0) \oplus (x_1 \wedge y_1) \oplus \cdots \oplus (x_{n-1} \wedge y_{n-1}) \big) \\
&\qquad \oplus \big( (x_0^{\prime} \wedge y_0) \oplus (x_1^{\prime} \wedge y_1) \oplus \cdots \oplus (x_{n-1}^{\prime} \wedge y_{n-1}) \big) \\
&= \langle \mathbf{x}, \mathbf{y} \rangle \oplus \langle \mathbf{x}^{\prime}, \mathbf{y} \rangle \\
\end{align}
$$
Similarly,
$$
\begin{align}
\langle \mathbf{x}, \mathbf{y} \oplus \mathbf{y}^{\prime} \rangle = \langle \mathbf{x}, \mathbf{y} \rangle \oplus \langle \mathbf{x}, \mathbf{y}^{\prime} \rangle \\
\end{align}
$$
Let $\mathbf{0} = \{ \underbrace{0, 0, \cdots, 0}_{n} \} = 0^n$, we have
$$
\begin{align}
\langle \mathbf{0}, \mathbf{y} \rangle = 0 \\
\langle \mathbf{x}, \mathbf{0} \rangle = 0 \\
\end{align}
$$
Hadamard Operator
Most of the important properties of Hadamard operator have been derived in the prerequisites section of my previous blog post on Deutsch-Jozsa algorithm. Unlike Deutsch-Jozsa algorithm, Simon’s algorithm is only going to use a small fraction of the Hadamard operator properties that Deutsch-Jozsa algorithm has used. I would just copy the properties useful for Simon’s algorithm algorithm. For the derivation, proof, and other properties of Hadamard operator, the reader should refer to my previous blog post.
To extract an arbitrary column $j$ from $H^{\otimes {n}}$, we prepared a one-hot quantum system basic state vector $| \mathbf{y} \rangle = [y_0, y_1, \cdots, y_{2^n-1}]^{\top}$, where $y_j = 1$ and $y_k = 0$ for $k \neq j$.
$$
\begin{align}
&H^{\otimes {n}}_{:,j} \\
&= H^{\otimes {n}} | \mathbf{y} \rangle \\
&= H^{\otimes n}[\mathbf{0}, \mathbf{j}] | \mathbf{x}_0 \rangle + H^{\otimes n}[\mathbf{1}, \mathbf{j}] | \mathbf{x}_1 \rangle + \cdots \\
&\qquad + H^{\otimes n}[\mathbf{2^n-1}, \mathbf{j}] | \mathbf{x}_{2^{n}-1} \rangle \\
&= \frac{1}{\sqrt{2^n}} (-1)^{\langle \mathbf{0}, \mathbf{j} \rangle} | \mathbf{x}_0 \rangle + \frac{1}{\sqrt{2^n}} (-1)^{\langle \mathbf{1}, \mathbf{j} \rangle} | \mathbf{x}_1 \rangle + \cdots \\
&\qquad + \frac{1}{\sqrt{2^n}} (-1)^{\langle \mathbf{2^n-1}, \mathbf{j} \rangle} | \mathbf{x}_{2^{n}-1} \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{i=0}^{2^n-1} (-1)^{\langle \mathbf{i}, \mathbf{j} \rangle} | \mathbf{x}_i \rangle\\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{x}, \mathbf{j} \rangle} | \mathbf{x} \rangle\\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{x}, \mathbf{y} \rangle} | \mathbf{x} \rangle\\
\end{align}
$$
where $| \mathbf{x}_i \rangle$ is a quantum system one-hot basic state vector, $|\mathbf{x}_i\rangle = [x_0, x_1, \cdots, x_{2^{n}-1}]^{\top}$, where $x_i = 1$ and $x_k = 0$ for $k \neq i$.
Specifically, if $j = 0$, $| \mathbf{y} \rangle = [\underbrace{1, 0, 0, \cdots, 0}_{2^n} ]^{\top} = | \mathbf{0} \rangle$,
$$
\begin{align}
H^{\otimes {n}} | \mathbf{0} \rangle
&= \frac{1}{\sqrt{2^n}} \sum_{i=0}^{2^n-1} (-1)^{\langle \mathbf{i}, \mathbf{0} \rangle} | \mathbf{x}_i \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{i=0}^{2^n-1} (-1)^{0} | \mathbf{x}_i \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{i=0}^{2^n-1} | \mathbf{x}_i \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x} \rangle \\
\end{align}
$$
Simon’s Problem
Simon’s problem is defined as the follows. Given a black box function $f: \{0,1\}^n \rightarrow \{0,1\}^n$, we are further assured that there exists a hidden binary string $\mathbf{c} \in \{0,1\}^n$, such that, for all $\mathbf{x}, \mathbf{y} \in \{0,1\}^n$,
$$
f(\mathbf{x}) = f(\mathbf{y}) \Leftrightarrow \mathbf{y} = \mathbf{x} \oplus \mathbf{c}
$$
where $\oplus$ is (bit-wise) $\text{XOR}$ (binary addition modulo 2).
Our goal is to find out what $\mathbf{c}$ is.
Mapping Properties
There are some properties of the mapping $f$. $f$ is either a one-to-one or two-to-one mapping.
$\mathbf{c} = \mathbf{0}$ $\Leftrightarrow$ $f$ is a one-to-one mapping
Proof
For $f$ is a one-to-one mapping $\Rightarrow$ $\mathbf{c} = \mathbf{0}$, it is too trivial to prove.
For $\mathbf{c} = \mathbf{0}$ $\Rightarrow$ $f$ is a one-to-one mapping, we would like to prove by contradiction.
If $\mathbf{c} = \mathbf{0}$ and $f$ is not a one-to-one mapping, there must exists $\mathbf{x}$ and $\mathbf{y}$, $\mathbf{x} \neq \mathbf{y}$, and $f(\mathbf{x}) = f(\mathbf{y})$. According to the assurance, $\mathbf{y} = \mathbf{x} \oplus \mathbf{c} = \mathbf{x} \oplus \mathbf{0} = \mathbf{x}$. This raises contradiction and therefore $f$ has to be a one-to-one mapping when $\mathbf{c} = \mathbf{0}$.
This concludes the proof.
$\mathbf{c} \neq \mathbf{0}$ $\Leftrightarrow$ $f$ is a two-to-one mapping.
Proof
For $f$ is a two-to-one mapping $\Rightarrow$ $\mathbf{c} \neq \mathbf{0}$, it is too trivial to prove.
For $\mathbf{c} \neq \mathbf{0}$ $\Rightarrow$ $f$ is a two-to-one mapping, we would like to prove by contradiction.
If $\mathbf{c} \neq \mathbf{0}$, for any $\mathbf{x}$, we must have $\mathbf{y}$, where $\mathbf{y} = \mathbf{x} \oplus \mathbf{c}$ and $\mathbf{x} \neq \mathbf{y}$, $f(\mathbf{x}) = f(\mathbf{y})$. So $f$ is at least a two-to-one mapping. Assuming there exists a tuple of $\mathbf{x}$, $\mathbf{y}$, and $\mathbf{z}$, where $\mathbf{y} = \mathbf{x} \oplus \mathbf{c}$, $\mathbf{z} \neq \mathbf{x}$, and $\mathbf{z} \neq \mathbf{y}$, and $f(\mathbf{x}) = f(\mathbf{y}) = f(\mathbf{z})$. According to the assurance, $\mathbf{z} = \mathbf{x} \oplus \mathbf{c}$. But $\mathbf{x} \oplus \mathbf{c} = \mathbf{y}$ so we have $\mathbf{z} = \mathbf{y}$. This raises contradiction and therefore $f$ has to be a two-to-one mapping when $\mathbf{c} \neq \mathbf{0}$.
This concludes the proof.
Trivial Solution
Solving Simon’s problem could be trivial.
If we happen to know any $\mathbf{x}$ and $\mathbf{y}$, where $\mathbf{x} \neq \mathbf{y}$ and $f(\mathbf{x}) = f(\mathbf{y})$, we immediately know $\mathbf{c} \neq \mathbf{0}$ and $\mathbf{c} = \mathbf{x} \oplus \mathbf{y}$. This is because,
$$
\begin{align}
\mathbf{x} \oplus \mathbf{y} &= \mathbf{x} \oplus ( \mathbf{x} \oplus \mathbf{c} ) \\
&= ( \mathbf{x} \oplus \mathbf{x} ) \oplus \mathbf{c} \\
&= \mathbf{0} \oplus \mathbf{c} \\
&= \mathbf{c} \\
\end{align}
$$
If we have checked all $\mathbf{x}, \mathbf{y} \in \{0,1\}^n$ and found there are no $\mathbf{x}$ and $\mathbf{y}$, where $\mathbf{x} \neq \mathbf{y}$ and $f(\mathbf{x}) = f(\mathbf{y})$, we immediately know $\mathbf{c} = \mathbf{0}$.
So the trivial solution for solving Simon’s problem is to evaluate $f$ using the values in $\{0,1\}^n$ one by one, and check if the newly evaluated valued has been shown in the previous evaluations.
Asymptotic Complexity for Trivial Solution
Using hashing, we should be able to check if the newly evaluated valued has been shown in the previous evaluations in $O(1)$. However, most of the computational cost comes from evaluating $f$ using the values in $\{0,1\}^n$ one by one.
If $\mathbf{c} \neq \mathbf{0}$, if we are extremely lucky and the first two evaluated values $f(\mathbf{x}_0) = f(\mathbf{x}_1)$, then we are done and $\mathbf{c} = \mathbf{x}_0 \oplus \mathbf{x}_1$. However, in the worst scenario, we would have to have evaluate $2^{n-1} + 1$ of the values in $\{0,1\}^n$.
If $\mathbf{c} = \mathbf{0}$, we would know it after evaluating $2^{n-1} + 1$ of the values in $\{0,1\}^n$ by realizing that there are no two evaluated values are the same.
Therefore, using the trivial solution, in the worst scenario, we would have to run the evaluation $2^{n-1} + 1$ times to determine the value of $\mathbf{c}$.
So the question is, can we do better?
Simon’s Algorithm
Design Quantum Circus
Similar to the quantum gates we used for the Deutsch algorithm and the Deutsch-Jozsa algorithm, the black-box $f(\mathbf{x})$ is represented using a quantum gate $U_f$.
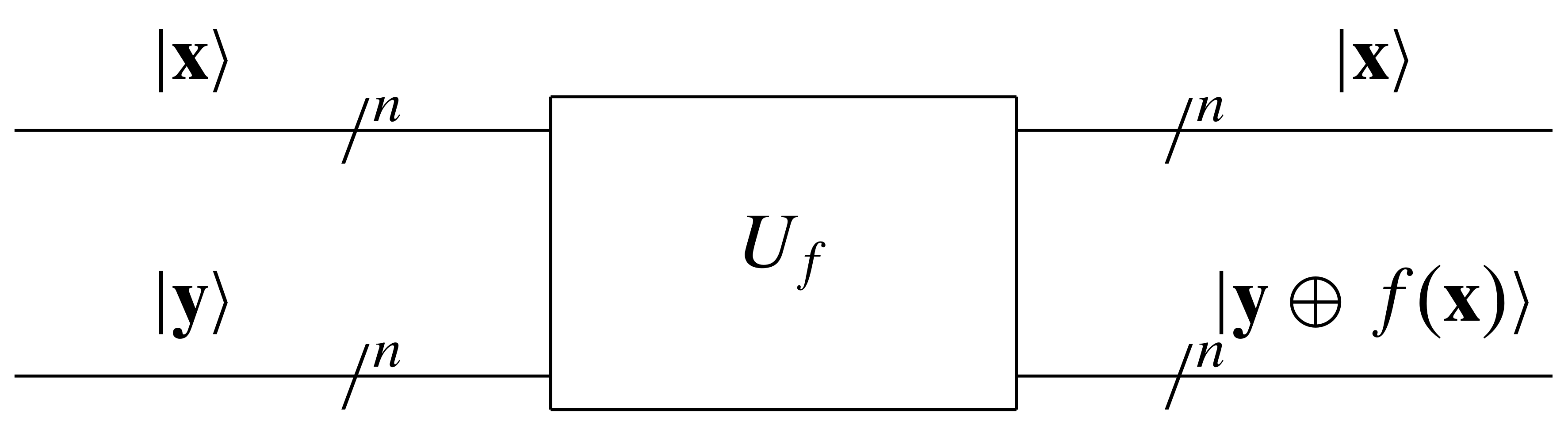
The quantum gate $U_f$ is a unitary matrix which maps from $| \mathbf{x} \rangle \otimes | \mathbf{y} \rangle$ to $| \mathbf{x} \rangle \otimes | f(\mathbf{x}) \oplus \mathbf{y} \rangle$, namely $U_f (| \mathbf{x} \rangle \otimes | \mathbf{y} \rangle) = | \mathbf{x} \rangle \otimes | f(\mathbf{x}) \oplus \mathbf{y} \rangle$, for $\mathbf{x} \in \{0, 1\}^n$ and $\mathbf{y} \in \{0, 1\}^n$. When $\mathbf{y} = \mathbf{0}$, $| f(\mathbf{x}) \oplus \mathbf{y} \rangle = | f(\mathbf{x}) \oplus \mathbf{0} \rangle = | f(\mathbf{x}) \rangle $, $| \mathbf{y} \oplus f(\mathbf{x}) \rangle$ is just $| f(\mathbf{x}) \rangle$.
Note that the above mapping is not necessarily valid when $| \mathbf{x} \rangle$ and $| \mathbf{y} \rangle$ are superpositions.
Let’s further check if we could achieve fewer runs with superpositions and $U_f$.
We have the following quantum circus. Let’s compute the each of the quantum states in the circus. The mathematics is actually much easier compared to the ones in the Deutsch-Jozsa algorithm.
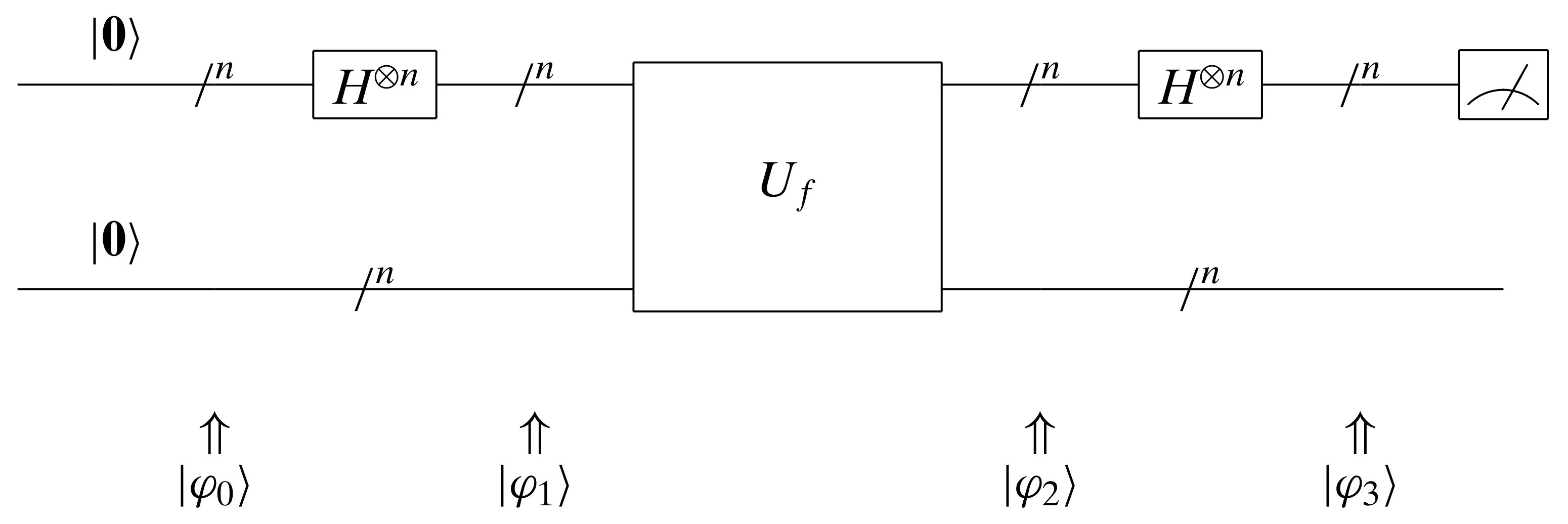
$$
\begin{align}
|\varphi_0\rangle &= |\mathbf{0}\rangle \otimes |\mathbf{0}\rangle\\
&= |\mathbf{0}, \mathbf{0}\rangle \\
\end{align}
$$
$$
\begin{align}
|\varphi_1\rangle &= (H^{\otimes n} \otimes I) |\varphi_0\rangle \\
&= (H^{\otimes n} \otimes I) (|\mathbf{0}\rangle \otimes |\mathbf{0}\rangle) \\
&= H^{\otimes n}|\mathbf{0}\rangle \otimes I | \mathbf{0} \rangle \\
&= \bigg( \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x} \rangle \bigg) \otimes | \mathbf{0} \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x} \rangle \otimes | \mathbf{0} \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x}, \mathbf{0} \rangle \\
\end{align}
$$
$$
\begin{align}
|\varphi_2\rangle &= U_f |\varphi_1\rangle \\
&= U_f \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x}, \mathbf{0} \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } U_f | \mathbf{x}, \mathbf{0} \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x} \rangle \otimes ( | \mathbf{0} \oplus f(\mathbf{x}) \rangle ) \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x} \rangle \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x}, f(\mathbf{x}) \rangle \\
\end{align}
$$
$$
\begin{align}
|\varphi_3\rangle &= (H^{\otimes n} \otimes I) |\varphi_2\rangle \\
&= (H^{\otimes n} \otimes I) \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x}, f(\mathbf{x}) \rangle \\
&= (H^{\otimes n} \otimes I) \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x}, f(\mathbf{x}) \rangle \\
&= \frac{1}{\sqrt{2^n}} (H^{\otimes n} \otimes I) \sum_{ \mathbf{x} \in \{0,1\}^n } | \mathbf{x} \rangle \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } (H^{\otimes n} \otimes I) (| \mathbf{x} \rangle \otimes | f(\mathbf{x}) \rangle) \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } H^{\otimes n} | \mathbf{x} \rangle \otimes I | f(\mathbf{x}) \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } H^{\otimes n} | \mathbf{x} \rangle \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{x} \in \{0,1\}^n } \bigg( \frac{1}{\sqrt{2^n}} \sum_{ \mathbf{z} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | \mathbf{z} \rangle \bigg) \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{z} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | \mathbf{z} \rangle \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{z} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | \mathbf{z}, f(\mathbf{x}) \rangle \\
\end{align}
$$
Suppose $\mathbf{x}_2 = \mathbf{x}_1 \oplus \mathbf{c}$, and we also have $\mathbf{x}_1 = \mathbf{x}_2 \oplus \mathbf{c}$. Because
$$
\begin{align}
&(-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} | \mathbf{z}, f(\mathbf{x}_1) \rangle \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_1) \rangle + | \mathbf{z}, f(\mathbf{x}_1) \rangle \big) \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_1) \rangle + | \mathbf{z}, f(\mathbf{x}_1 \oplus \mathbf{c}) \rangle \big) \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_1) \rangle + | \mathbf{z}, f(\mathbf{x}_2) \rangle \big) \\
\end{align}
$$
$$
\begin{align}
&(-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} | \mathbf{z}, f(\mathbf{x}_2) \rangle \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_2) \rangle + | \mathbf{z}, f(\mathbf{x}_2) \rangle \big) \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_2) \rangle + | \mathbf{z}, f(\mathbf{x}_2 \oplus \mathbf{c}) \rangle \big) \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_2) \rangle + | \mathbf{z}, f(\mathbf{x}_1) \rangle \big) \\
\end{align}
$$
$$
\begin{align}
& (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} | \mathbf{z}, f(\mathbf{x}_1) \rangle + (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} | \mathbf{z}, f(\mathbf{x}_2) \rangle \\
&= \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_1) \rangle + | \mathbf{z}, f(\mathbf{x}_2) \rangle \big) + \frac{1}{2} (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} \big( | \mathbf{z}, f(\mathbf{x}_2) \rangle + | \mathbf{z}, f(\mathbf{x}_1) \rangle \big) \\
&= \frac{(-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle}}{2} | \mathbf{z}, f(\mathbf{x}_1) \rangle + \frac{(-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle}}{2} | \mathbf{z}, f(\mathbf{x}_2) \rangle \\
&= \frac{(-1)^{\langle \mathbf{z}, \mathbf{x}_1 \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x}_1 \oplus \mathbf{c} \rangle}}{2} | \mathbf{z}, f(\mathbf{x}_1) \rangle + \frac{(-1)^{\langle \mathbf{z}, \mathbf{x}_2 \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x}_2 \oplus \mathbf{c} \rangle}}{2} | \mathbf{z}, f(\mathbf{x}_2) \rangle \\
\end{align}
$$
We could further rearrange $|\varphi_3\rangle $,
$$
\begin{align}
& |\varphi_3\rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{z} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x} \oplus \mathbf{c} \rangle}}{2} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle \oplus \langle \mathbf{z}, \mathbf{c} \rangle} }{2} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} + (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle + \langle \mathbf{z}, \mathbf{c} \rangle} }{2} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | \mathbf{z}, f(\mathbf{x}) \rangle \\
\end{align}
$$
Note that $\langle \mathbf{z}, \mathbf{c} \rangle$ is a binary value. When $\langle \mathbf{z}, \mathbf{c} \rangle = 1$, $\sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} = 0$, which means that for the top output qubits, we have exact zero probability of observing $\mathbf{z}$. We could only observe $\mathbf{z}$ whose $\langle \mathbf{z}, \mathbf{c}\rangle = 0$ for the top output qubits.
Statistically, when $\mathbf{c} = 0$, $\langle \mathbf{z}, \mathbf{c}\rangle = 0$, for all $\mathbf{z} \in \{0,1\}^2$. This means all $\mathbf{z}$ are possible to be observed from the top output qubits. So what is the probability of observing $\mathbf{z}$, $p(\mathbf{z})$? Is it uniformly distributed?
$$
\begin{align}
|\varphi_3\rangle
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | \mathbf{z}\rangle \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } | \mathbf{z}\rangle \otimes \Bigg( \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg) \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } | \mathbf{z}\rangle \otimes \Bigg( \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Bigg) \\
\end{align}
$$
$$
\begin{align}
p(\mathbf{z}) &= \frac{\Big\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Big\rvert^2}{ \sum_{ \mathbf{z} \in \{0,1\}^n } \Big\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Big\rvert^2}
\end{align}
$$
Because $\mathbf{c} = 0$ and $f$ is an one-to-one mapping, we have
$$
\begin{align}
\langle f(\mathbf{x}), f(\mathbf{y}) \rangle =
\begin{cases}
1 & \text{when $\mathbf{x} = \mathbf{y}$}\\
0 & \text{when $\mathbf{x} \neq \mathbf{y}$}\\
\end{cases}
\end{align}
$$
$$
\begin{align}
& \Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Bigg\rvert^2 \\
&= \Bigg\langle \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle, \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Bigg\rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{y} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} (-1)^{\langle \mathbf{z}, \mathbf{y} \rangle} \langle f(\mathbf{x}), f(\mathbf{y}) \rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \langle f(\mathbf{x}), f(\mathbf{x}) \rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } 1 \\
&= 2^n \\
\end{align}
$$
$$
\begin{align}
\sum_{ \mathbf{z} \in \{0,1\}^n } \Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Bigg\rvert^2
&= 2^n 2^n\\
&= 2^{2n}\\
\end{align}
$$
$$
\begin{align}
p(\mathbf{z}) &= \frac{\Big\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Big\rvert^2}{ \sum_{ \mathbf{z} \in \{0,1\}^n } \Big\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } (-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} | f(\mathbf{x}) \rangle \Big\rvert^2} \\
&= \frac{2^n}{2^{2n}} \\
&= \frac{1}{2^n} \\
\end{align}
$$
So when $\mathbf{c} = 0$, $p(\mathbf{z})$ is a uniform distribution and $p(\mathbf{z}) = \frac{1}{2^n}$.
How about when $\mathbf{c} \neq 0$?
$$
\begin{align}
& |\varphi_3\rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | \mathbf{z}, f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | \mathbf{z}\rangle \otimes | f(\mathbf{x}) \rangle \\
&= \frac{1}{2^n} \sum_{ \mathbf{z} \in \{0,1\}^n } | \mathbf{z}\rangle \otimes \Bigg( \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg) \\
\end{align}
$$
$$
\begin{align}
p(\mathbf{z}) &= \frac{ \Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg\rvert^2 }{ \sum_{ \mathbf{z} \in \{0,1\}^n } \Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg\rvert^2}
\end{align}
$$
Because $\mathbf{c} \neq 0$ and $f$ is a two-to-one mapping, we have
$$
\begin{align}
\langle f(\mathbf{x}), f(\mathbf{y}) \rangle =
\begin{cases}
1 & \text{when $\mathbf{x} = \mathbf{y}$ or $\mathbf{x} = \mathbf{y} \oplus \mathbf{c} $ }\\
0 & \text{else}\\
\end{cases}
\end{align}
$$
$$
\begin{align}
& \Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg\rvert^2 \\
&= \Bigg\langle \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle, \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg\rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{y} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} \frac{(-1)^{\langle \mathbf{z}, \mathbf{y} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} \langle f(\mathbf{x}), f(\mathbf{y}) \rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{y} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \oplus \mathbf{y} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big)^2 }{4} \langle f(\mathbf{x}), f(\mathbf{y}) \rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } \sum_{ \mathbf{y} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big)^2 }{4} \langle f(\mathbf{x}), f(\mathbf{y}) \rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big)^2 }{4} \langle f(\mathbf{x}), f(\mathbf{x}) \rangle \\
&\qquad + \frac{(-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big)^2 }{4} \langle f(\mathbf{x}), f(\mathbf{x} + \mathbf{c}) \rangle \\
&= \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big)^2 }{2} \\
&=
\begin{cases}
2^n & \text{when $\langle \mathbf{z}, \mathbf{c} \rangle = 0$}\\
0 & \text{when $\langle \mathbf{z}, \mathbf{c} \rangle = 1$}\\
\end{cases}
\end{align}
$$
In short,
$$
\begin{align}
\Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg\rvert^2
&=
\begin{cases}
2^n & \text{when $\langle \mathbf{z}, \mathbf{c} \rangle = 0$}\\
0 & \text{when $\langle \mathbf{z}, \mathbf{c} \rangle = 1$}\\
\end{cases}
\end{align}
$$
Similarly,
$$
\begin{align}
\sum_{ \mathbf{z} \in \{0,1\}^n } \Bigg\lvert \sum_{ \mathbf{x} \in \{0,1\}^n } \frac{(-1)^{\langle \mathbf{z}, \mathbf{x} \rangle} \big( 1 + (-1)^{\langle \mathbf{z}, \mathbf{c} \rangle} \big) }{2} | f(\mathbf{x}) \rangle \Bigg\rvert^2
&= 2^{n-1} 2^n\\
&= 2^{2n - 1}\\
\end{align}
$$
Taken together, when $\mathbf{c} \neq 0$,
$$
\begin{align}
p(\mathbf{z}) =
\begin{cases}
\frac{1}{2^{n-1}} & \text{when $\langle \mathbf{z}, \mathbf{c} \rangle = 0$}\\
0 & \text{when $\langle \mathbf{z}, \mathbf{c} \rangle = 1$}\\
\end{cases}
\end{align}
$$
Now, suppose we run the circus and observe the top output qubits $k$ times, we observed $\mathbf{z}_0$, $\mathbf{z}_1$, $\cdots$, $\mathbf{z}_{k-1}$. We now know that $\langle \mathbf{z}_i, \mathbf{c} \rangle = 0$ for $i \in [0, k-1]$.
Computing $\mathbf{c}$ is like solving linear equations. Let’s see how to do it.
Run Quantum Circus and Post Processing
In conventional linear algebra, to solve linear equations that have $n$ variables, we would need to have $n$ linearly independent linear equations. This also applies to solving linear equations in binary vector space.
In our particular problem, $\mathbf{c}$ is a binary vector that contains $n$ variables, $\{ \mathbf{c}_0, \mathbf{c}_1, \cdots, \mathbf{c}_{n-1} \}$, it turns out that we would need $n - 1$ linearly independent $\mathbf{z}_i$ such that $\langle \mathbf{z}_i, \mathbf{c} \rangle = 0$ to solve $\mathbf{c}$. (Actually, when $\mathbf{c} \neq 0$, we could only find at most $n - 1$ linearly independent $\mathbf{z}_i$)
In the context of linear dependency in binary vector space, we say the set of binary vectors are linearly dependent if at least one of the binary vectors can be defined as a linear combination of others. The no binary vector could be written in this way, then the binary vectors are linearly independent.
Given binary vectors $\mathbf{z}_0$, $\mathbf{z}_1$, $\cdots$ and $\mathbf{z}_{n-1}$, and boolean values $b_0$, $b_1$, $\cdots$, $b_{n-1}$, we say $\mathbf{z}_0$, $\mathbf{z}_1$, $\cdots$ and $\mathbf{z}_{n-1}$ are linearly independent, if
$$
\begin{align}
( b_0 \wedge \mathbf{z}_0 ) \oplus ( b_1 \wedge \mathbf{z}_1 ) \oplus ( b_2 \wedge \mathbf{z}_2 ) \oplus \cdots \oplus ( b_{n-1} \wedge \mathbf{z}_{n-1} ) = \mathbf{0}
\end{align}
$$
has only trivial solution $b_0 = b_1 = \cdots = b_{n-1} = 0$. Otherwise, $\mathbf{z}_0$, $\mathbf{z}_1$, $\cdots$ and $\mathbf{z}_{n-1}$ are linearly dependent.
This also suggests, to become linearly independent, $\mathbf{z}_i \neq \mathbf{0}$, for $i \in [1, n-1]$.
Suppose $\mathbf{z}_0$, $\mathbf{z}_1$, $\cdots$ and $\mathbf{z}_{n-1}$ are linearly dependent, at least one of the $n$ linear equations, $\langle \mathbf{z}_0, \mathbf{c} \rangle = 0$, $\langle \mathbf{z}_1, \mathbf{c} \rangle = 0$, $\cdots$, $\langle \mathbf{z}_n, \mathbf{c} \rangle = 0$, would be redundant.
$$
\begin{align}
0 &= \langle \mathbf{0}, \mathbf{c} \rangle \\
&= \langle ( b_0 \wedge \mathbf{z}_0 ) \oplus ( b_1 \wedge \mathbf{z}_1 ) \oplus ( b_2 \wedge \mathbf{z}_2 ) \oplus \cdots \\
&\qquad \oplus ( b_{n-1} \wedge \mathbf{z}_{n-1} ), \mathbf{c} \rangle \\
&= \langle b_0 \wedge \mathbf{z}_0, \mathbf{c} \rangle \oplus \langle b_1 \wedge \mathbf{z}_1, \mathbf{c} \rangle \oplus \langle b_2 \wedge \mathbf{z}_2, \mathbf{c} \rangle \oplus \cdots \\
&\qquad \oplus \langle b_{n-1} \wedge \mathbf{z}_{n-1}, \mathbf{c} \rangle \\
&= ( b_0 \wedge \langle \mathbf{z}_0, \mathbf{c} \rangle ) \oplus ( b_1 \wedge \langle \mathbf{z}_1, \mathbf{c} \rangle ) \oplus ( b_2 \wedge \langle \mathbf{z}_2, \mathbf{c} \rangle ) \oplus \cdots \\
&\qquad \oplus ( b_{n-1} \wedge \langle \mathbf{z}_{n-1}, \mathbf{c} \rangle ) \\
\end{align}
$$
Since $\mathbf{z}_0$, $\mathbf{z}_1$, $\cdots$ and $\mathbf{z}_{n-1}$ are linearly dependent, without loss of generality, assuming $b_i \neq 0$ ($b_i = 1$).
$$
\begin{align}
\langle \mathbf{z}_i, \mathbf{c} \rangle
&=b_i \wedge \langle \mathbf{z}_i, \mathbf{c} \rangle \\
&= (b_i \wedge \langle \mathbf{z}_i, \mathbf{c} \rangle) \oplus 0\\
&= (b_i \wedge \langle \mathbf{z}_i, \mathbf{c} \rangle) \oplus ( b_0 \wedge \langle \mathbf{z}_0, \mathbf{c} \rangle ) \oplus ( b_1 \wedge \langle \mathbf{z}_1, \mathbf{c} \rangle ) \oplus \\
&\qquad ( b_2 \wedge \langle \mathbf{z}_2, \mathbf{c} \rangle ) \oplus \cdots \oplus ( b_{n-1} \wedge \langle \mathbf{z}_{n-1}, \mathbf{c} \rangle ) \\
&= (b_i \wedge \langle \mathbf{z}_i, \mathbf{c} \rangle) \oplus (b_i \wedge \langle \mathbf{z}_i, \mathbf{c} \rangle) \oplus \bigoplus_{j \neq i}^{} (b_j \wedge \langle \mathbf{z}_j, \mathbf{c} \rangle) \\
&= 0 \oplus \bigoplus_{j \neq i}^{} (b_j \wedge \langle \mathbf{z}_j, \mathbf{c} \rangle) \\
&= \bigoplus_{j \neq i}^{} (b_j \wedge \langle \mathbf{z}_j, \mathbf{c} \rangle) \\
&= \bigoplus_{j \neq i}^{} (b_j \wedge 0) \\
&= \bigoplus_{j \neq i}^{} 0 \\
&= 0 \\
\end{align}
$$
Therefore, $\langle \mathbf{z}_i, \mathbf{c} \rangle $ in the $n$ linear equations will be redundant.
Given $n - 1$ linearly independent binary vectors, let’s further see how to solve linear equations in the binary vector space. The process is similar to Gaussian elimination used for solving conventional linear equations.
Let’s start with an example, where $n=3$. $\mathbf{z}_0 = \{1,0,1\}$, $\mathbf{z}_1 = \{1,1,1\}$. It is easy to verify that $\mathbf{z}_0$, $\mathbf{z}_1$ are linearly independent. Because, $\langle \mathbf{z}_0, \mathbf{c} \rangle = 0$, $\langle \mathbf{z}_1, \mathbf{c} \rangle = 0$,
$$
\begin{align}
\langle \mathbf{z}_0, \mathbf{c} \rangle = (1 \wedge \mathbf{c}_0) \oplus (0 \wedge \mathbf{c}_1) \oplus (1 \wedge \mathbf{c}_2) = 0 \\
\langle \mathbf{z}_1, \mathbf{c} \rangle = (1 \wedge \mathbf{c}_0) \oplus (1 \wedge \mathbf{c}_1) \oplus (1 \wedge \mathbf{c}_2) = 0 \\
\end{align}
$$
We could eliminate $(1 \wedge \mathbf{c}_0)$ by $\langle \mathbf{z}_0, \mathbf{c} \rangle \oplus \langle \mathbf{z}_1, \mathbf{c} \rangle$, we then have
$$
\begin{align}
& \langle \mathbf{z}_0, \mathbf{c} \rangle \oplus \langle \mathbf{z}_1, \mathbf{c} \rangle \\
&= (1 \wedge \mathbf{c}_0) \oplus (0 \wedge \mathbf{c}_1) \oplus (1 \wedge \mathbf{c}_2) (1 \wedge \mathbf{c}_0) \oplus (1 \wedge \mathbf{c}_1) \oplus (1 \wedge \mathbf{c}_2)\\
&= (0 \wedge \mathbf{c}_1) \oplus (1 \wedge \mathbf{c}_1) \\
&= (0 \oplus 1) \wedge \mathbf{c}_1 \\
&= 1 \wedge \mathbf{c}_1 \\
&= \mathbf{c}_1 \\
&= 0 \\
\end{align}
$$
So $\mathbf{c}_1 = 0$.
In addition, we have
$$
\begin{align}
\langle \mathbf{z}_1, \mathbf{c} \rangle
&= (1 \wedge \mathbf{c}_0) \oplus (1 \wedge \mathbf{c}_1) \oplus (1 \wedge \mathbf{c}_2) \\
&= \mathbf{c}_0 \oplus \mathbf{c}_2
\end{align}
$$
So $\mathbf{c}_0 = \mathbf{c}_2 = 0$ or $\mathbf{c}_0 = \mathbf{c}_2 = 1$.
Therefore, we have two $\mathbf{c}$ possible, $\mathbf{c}^{\prime} = \{0,0,0\}$ or $\mathbf{c}^{\prime\prime} = \{1,0,1\}$.
We could also see that solving the $n-1$ linear equations always results in a $\mathbf{c}^{\prime} = \mathbf{0}$ and another non-zero $\mathbf{c}^{\prime\prime}$.
How do we determine whether $\mathbf{c}^{\prime} = \mathbf{0}$ or $\mathbf{c}^{\prime\prime}$ is the correct solution? We run the circuit once to get the value for $f(\mathbf{0})$ and $f(\mathbf{c}^{\prime\prime})$. If $f(\mathbf{c}^{\prime\prime}) = f(\mathbf{0})$, $\mathbf{c} = \mathbf{c}^{\prime\prime}$. If $f(\mathbf{c}^{\prime\prime}) \neq f(\mathbf{0})$, $\mathbf{c} = \mathbf{0}$.
Algorithm Analysis
The final question is what are the probabilities of observing $n-1$ linearly independent $\mathbf{z}$ in a few runs.
Let’s compute the probability of observing $n-1$ linearly independent $\mathbf{z}$ in $n-1$ runs.
Suppose $\mathbf{c} \neq 0$. For the first time $t=0$ we “draw” $\mathbf{z}$, we have to avoid $\mathbf{z}_{t=0} \neq \mathbf{0}$, such probability is $1 - \frac{1}{2^{n-1}}$. Once $\mathbf{z}_{t=0}$ is drawn, at $t=1$, we could draw $\mathbf{z}_{t=1}$ for anything but $\mathbf{z}_{t=0}$ and $\mathbf{0}$, such probability is $1 - \frac{1}{2^{n-2}}$; $\mathbf{z}_{t=0}$ and $\mathbf{z}_{t=1}$ forms a subspace that consists of $2^2 = 4$ vectors, if we draw $\mathbf{z}_{t=2}$ from this subspace, we would have linear dependencies. So at $t=2$, we have to avoid these $2^2 = 4$ vectors, such probability is $1 - \frac{1}{2^{n-3}}$. We iterate until we have drawn $n-1$ $\mathbf{z}$. The probability of observing $n-1$ linearly independent $\mathbf{z}$ in $n-1$ runs is
$$
\begin{align}
\prod_{i=1}^{n-1} \Big( 1 - \frac{1}{2^i} \Big)
\end{align}
$$
We notice that $(1-a)(1-b) \geq 1 - (a + b)$ for $a, b \in [0, 1]$.
$$
\begin{align}
\prod_{i=1}^{n-1} \Big( 1 - \frac{1}{2^i} \Big)
&= \frac{1}{2} \prod_{i=2}^{n-1} \Big( 1 - \frac{1}{2^i} \Big) \\
&\geq \frac{1}{2} \Big(1 - \sum_{i=2}^{n-1} \frac{1}{2^i} \Big) \\
&= \frac{1}{2} \Big(1 - \frac{1}{2} \big(1 - \frac{1}{2^{n-2}}\big) \Big) \\
&\geq \frac{1}{2} \Big(1 - \frac{1}{2} \Big) \\
&= \frac{1}{4} \\
\end{align}
$$
So Simon’s algorithm succeeds with probability of at least $\frac{1}{4}$. We could improve the probability of success via repeating this process many times.
Conclusion
Simon’s problem and algorithm is a combination of quantum mechanics and statistics. From here, we started to see how quantum computing started to solve problems that follows some statistical rules.
References
Simon's Algorithm