Deutsch's Algorithm
Introduction
Deutsch’s algorithm is the simplest quantum computing algorithm invented to solve a slightly contrived problem. Suppose we have a black-box function $f(x)$ which maps from the set $\{0,1\}$ to the set $\{0,1\}$. It is easy to speculate that there are four possible mappings for $f(x)$. We call the function $f(x)$ constant if $f(0) = f(1)$, otherwise we call the function $f(x)$ balanced.
With classical circuits, we would have to run the black-box $f(x)$ twice to evaluate $f(0)$ and $f(1)$ and compare the values of $f(0)$ and $f(1)$ to see if they are equivalent or not. With quantum circuits, because we could take advantage of superposition, probably we could do better with fewer runs and operations.
In this blog post, I would like to discuss the Deutsch’s algorithm.
Prerequisites
Separable and Entangled States
States that can be broken into the Kronecker product of states from the constituent subsystems are called separable states, whereas states that are unbreakable are referred to as entangled states.
For example, we have the following two states $| \psi \rangle$ and $| \psi^{\prime} \rangle$.
$$
\begin{align}
| \psi \rangle &= \frac{| 0, 0 \rangle - | 0, 1 \rangle + | 1, 0 \rangle - | 1, 1 \rangle}{2}\\
&= \frac{| 0\rangle \otimes | 0 \rangle - | 0\rangle \otimes | 1 \rangle + | 1\rangle \otimes | 0 \rangle - | 1\rangle \otimes | 1 \rangle}{2}\\
&= \frac{| 0 \rangle + | 1 \rangle}{\sqrt{2}} \otimes \frac{| 0 \rangle - | 1 \rangle}{\sqrt{2}} \\
| \psi^{\prime} \rangle &= \frac{| 0, 1 \rangle + | 1, 0 \rangle}{\sqrt{2}}\\
\end{align}
$$
$| \psi \rangle$ is separable and $| \psi^{\prime} \rangle$ is entangled.
Unitary Quantum Operator
Every quantum operator $U$ is unitary and thus reversible. Because $UU^{\dagger} = U^{\dagger}U = I$, we have
$$
\begin{align}
U^{\dagger} (U |\varphi\rangle) &= (U^{\dagger} U) |\varphi\rangle \\
&= I |\varphi\rangle \\
&= |\varphi\rangle \\
\end{align}
$$
Hadamard Operator
Hardmard operator is a special quantum operator.
$$
\begin{align}
H &=
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{bmatrix}
\end{align}
$$
Notice that $H^{\dagger} = H$, therefore
$$
\begin{align}
H^{\dagger} (H |\varphi\rangle) &= H (H |\varphi\rangle) \\
&= (H^2) |\varphi\rangle \\
&= I |\varphi\rangle \\
&= |\varphi\rangle \\
\end{align}
$$
$$
\begin{align}
H|0\rangle &=
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{bmatrix}
\begin{bmatrix}
1 \\
0 \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
\end{bmatrix} \\
&= \frac{|0\rangle + |1\rangle}{\sqrt{2}}
\end{align}
$$
$$
\begin{align}
H\frac{|0\rangle + |1\rangle}{\sqrt{2}} &= HH|0\rangle \\
&= I|0\rangle \\
&= |0\rangle \\
\end{align}
$$
$$
\begin{align}
H|1\rangle &=
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{bmatrix}
\begin{bmatrix}
0 \\
1 \\
\end{bmatrix} \\
&=
\begin{bmatrix}
\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} \\
\end{bmatrix} \\
&= \frac{|0\rangle - |1\rangle}{\sqrt{2}}
\end{align}
$$
$$
\begin{align}
H\frac{|0\rangle - |1\rangle}{\sqrt{2}} &= HH|1\rangle \\
&= I|1\rangle \\
&= |1\rangle \\
\end{align}
$$
Reducing Sum or Difference to Boolean
If $f(x)$ maps from the set $\{0,1\}$ to the set $\{0,1\}$, we have
$$
\begin{align}
(-1)^{f(1) - f(0)} = (-1)^{f(0) \oplus f(1)}
\end{align}
$$
Where $\oplus$ is $\text{XOR}$ (binary addition modulo 2).
Deutsch’s Algorithm
The black-box $f(x)$ is represented using a quantum gate $U_f$. Just like the classical gate for $f(x)$, it has four possible candidates. Our job is to determine whether the $f(x)$ corresponding to the $U_f$ is constant or balanced.
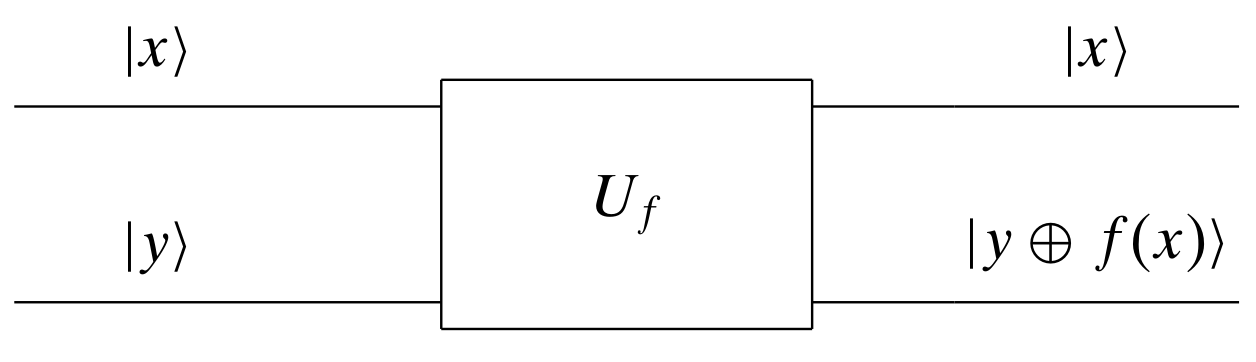
The quantum gate $U_f$ is a unitary matrix which maps from $| x \rangle \otimes | y \rangle$ to $| x \rangle \otimes | y \oplus f(x) \rangle$, namely $U_f (| x \rangle \otimes | y \rangle) = | x \rangle \otimes | y \oplus f(x) \rangle$, for $x, y \in \{0, 1\}$. When $y = 0$, $| y \oplus f(x) \rangle = | 0 \oplus f(x) \rangle = | f(x) \rangle $, $| y \oplus f(x) \rangle$ is just $| f(x) \rangle$.
Note that the above mapping is only valid when $| x \rangle$ and $| y \rangle$ are basic qubit states $| 0 \rangle$ or $| 1 \rangle$. When $| x \rangle$ and $| y \rangle$ are superpositions, the mapping does not necessarily hold.
Let’s further check when $| x \rangle$ and $| y \rangle$ are superpositions, what the outputs from $U_f$ will be. Perhaps we could achieve fewer runs with superpositions.
First Attempt
In the first attempt, we made the first qubit input to $U_f$ a superposition, which is achieved by applying a Hadamard operator to the input basic state $|0\rangle$. The superposition is
$$
\begin{align}
H|0\rangle &= \frac{|0\rangle + |1\rangle}{\sqrt{2}}
\end{align}
$$
The second qubit input to $U_f$ is just a normal basic state $|0\rangle$.
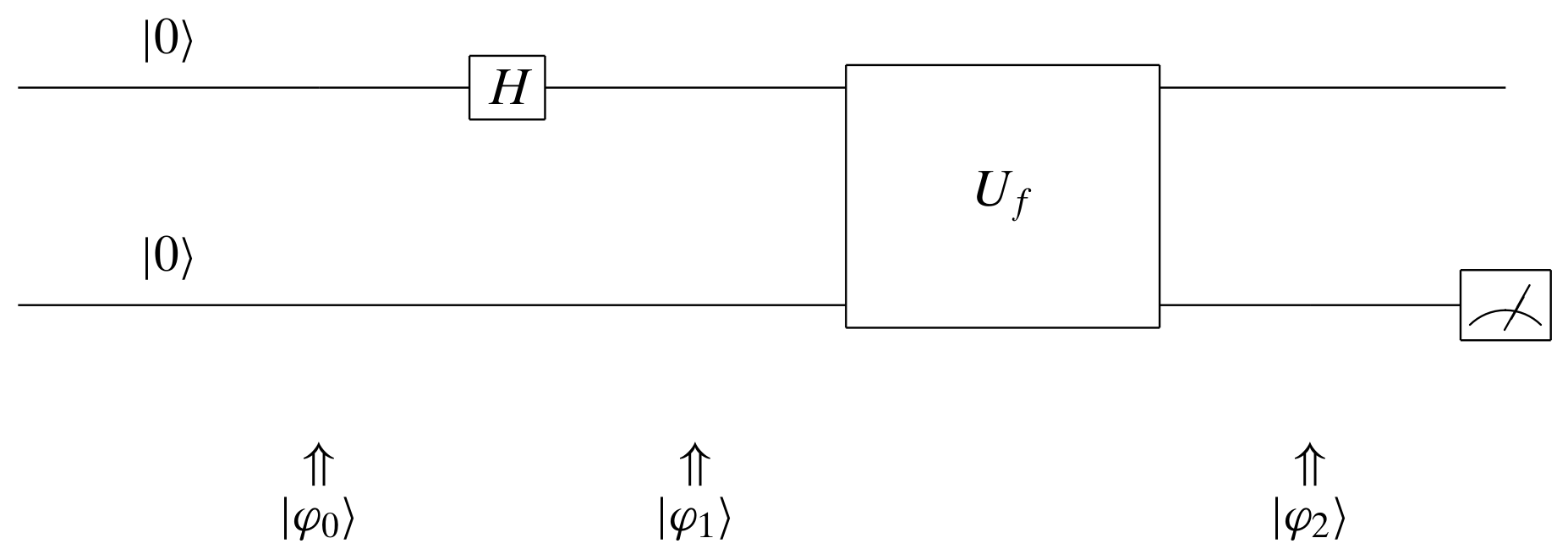
$$
\begin{align}
|\varphi_0\rangle &= |0\rangle \otimes |0\rangle\\
&= |0, 0\rangle \\
\end{align}
$$
$$
\begin{align}
|\varphi_1\rangle &= (H \otimes I) |\varphi_0\rangle \\
&= (H \otimes I) (|0\rangle \otimes |0\rangle) \\
&= H|0\rangle \otimes I |0\rangle \\
&= \frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes |0\rangle \\
&= \frac{|0\rangle \otimes |0\rangle + |1\rangle \otimes |0\rangle }{\sqrt{2}} \\
&= \frac{|0, 0\rangle + |1, 0\rangle}{\sqrt{2}} \\
\end{align}
$$
$$
\begin{align}
|\varphi_2\rangle &= U_f |\varphi_1\rangle \\
&= U_f \frac{|0, 0\rangle + |1, 0\rangle}{\sqrt{2}} \\
&= \frac{U_f |0, 0\rangle + U_f |1, 0\rangle}{\sqrt{2}} \\
&= \frac{U_f (|0\rangle \otimes |0\rangle) + U_f (|1\rangle \otimes |0\rangle)}{\sqrt{2}} \\
&= \frac{|0\rangle \otimes |0 \oplus f(0)\rangle + |1\rangle \otimes |0 \oplus f(1)\rangle}{\sqrt{2}} \\
&= \frac{|0\rangle \otimes |f(0)\rangle + |1\rangle \otimes |f(1)\rangle}{\sqrt{2}} \\
&= \frac{|0, f(0)\rangle + |1, f(1)\rangle}{\sqrt{2}} \\
\end{align}
$$
If $f(0) = 0$, $f(1) = 1$, one of the balanced cases,
$$
\begin{align}
|\varphi_2\rangle &= \frac{|0, 0\rangle + |1, 1\rangle}{\sqrt{2}} \\
\end{align}
$$
Note that this $|\varphi_2\rangle$ is entangled and could not be expressed as the Kronecker product of two qubits. The first qubit output from $U_f$ is not $H|0\rangle$ either. In fact it could not be described using single qubit! The two qubits must be described as a whole due to quantum entanglement. When we observe either the first qubit output or the second qubit output, we immediately know the observation of the other qubit. For example, if we observed the second qubit is 0, we know the observation of the first qubit must be 0. There are 50-50 percent chance observing 0 or 1 for both the first qubit and the second qubit.
If $f(0) = 1$, $f(1) = 0$, one of the balanced cases,
$$
\begin{align}
|\varphi_2\rangle &= \frac{|0, 1\rangle + |1, 0\rangle}{\sqrt{2}} \\
\end{align}
$$
This $|\varphi_2\rangle$ is entangled and there are 50-50 percent chance observing 0 or 1 for both the first qubit and the second qubit.
If $f(0) = 0$, $f(1) = 0$, one of the constant cases,
$$
\begin{align}
|\varphi_2\rangle &= \frac{|0, 0\rangle + |1, 0\rangle}{\sqrt{2}} \\
&= \frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes |0\rangle\\
&= \frac{-|0\rangle - |1\rangle}{\sqrt{2}} \otimes (-|0\rangle)\\
\end{align}
$$
This $|\varphi_2\rangle$ is separable. Although we are not sure the exact state the two qubit outputs would be in, due to the phase is not defined, we are sure that the observation of the bottom qubit must be 0.
If $f(0) = 1$, $f(1) = 1$, one of the constant cases,
$$
\begin{align}
|\varphi_2\rangle &= \frac{|0, 1\rangle + |1, 1\rangle}{\sqrt{2}} \\
&= \frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes |1\rangle\\
&= \frac{-|0\rangle - |1\rangle}{\sqrt{2}} \otimes (-|1\rangle)\\
\end{align}
$$
This $|\varphi_2\rangle$ is separable. Although we are not sure the exact state the two qubit outputs would be in, due to the phase is not defined, we are sure that the observation of the bottom qubit must be 1.
However, all of these are not helpful if we are only allowed to run once. After running once, no matter what we observed from the first qubit and the second qubit, we are not sure whether $f(x)$ is constant or balanced.
Second Attempt
In the second attempt, we made the second qubit input to $U_f$ a superposition, which is achieved by applying a Hadamard operator to the input basic state $|1\rangle$. The superposition is
$$
\begin{align}
H|1\rangle &= \frac{|0\rangle - |1\rangle}{\sqrt{2}}
\end{align}
$$
The second qubit input to $U_f$ is a variable and it could be either $|0\rangle$ or $|1\rangle$.
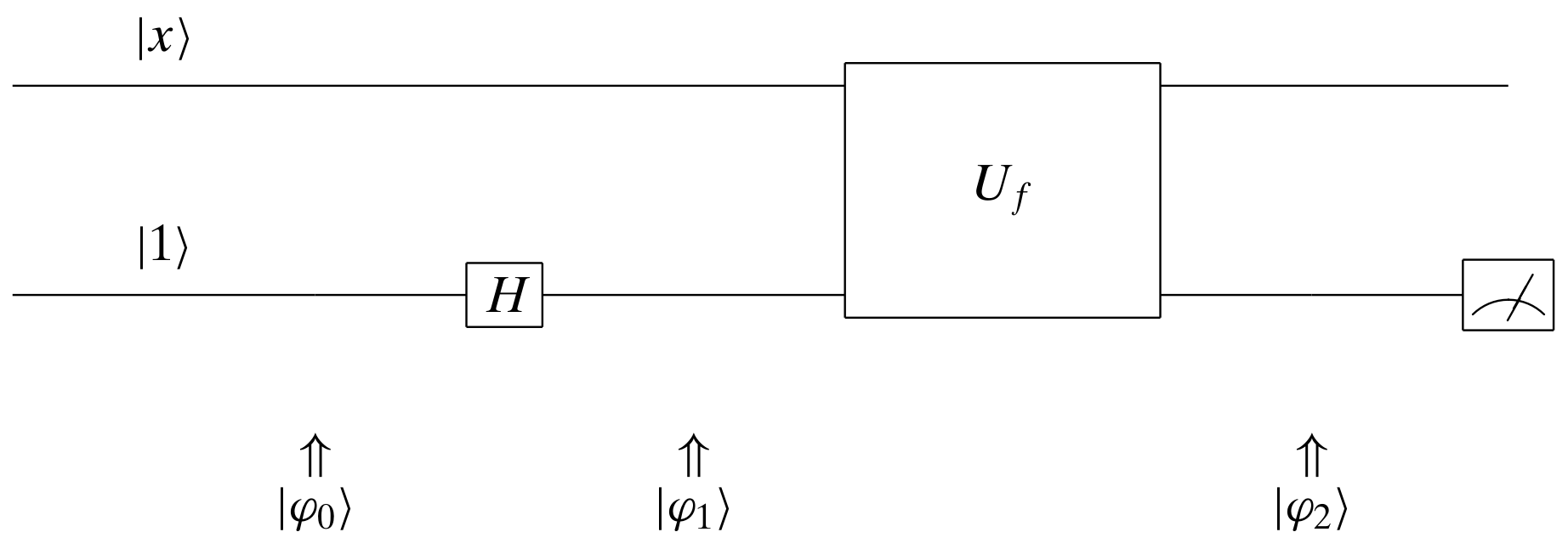
$$
\begin{align}
|\varphi_0\rangle &= |x\rangle \otimes |1\rangle\\
&= |x, 1\rangle \\
\end{align}
$$
$$
\begin{align}
|\varphi_1\rangle &= (I \otimes H) |\varphi_0\rangle \\
&= (I \otimes H) (|x\rangle \otimes |1\rangle) \\
&= I|x\rangle \otimes H |1\rangle \\
&= |x\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}} \\
&= \frac{|x, 0\rangle - |x, 1\rangle}{\sqrt{2}} \\
\end{align}
$$
$$
\begin{align}
|\varphi_2\rangle &= U_f |\varphi_1\rangle \\
&= U_f \frac{|x, 0\rangle - |x, 1\rangle}{\sqrt{2}} \\
&= \frac{U_f |x, 0\rangle - U_f |x, 1\rangle}{\sqrt{2}} \\
&= \frac{U_f (|x\rangle \otimes |0\rangle) - U_f (|x\rangle \otimes |1\rangle)}{\sqrt{2}} \\
&= \frac{|x\rangle \otimes |0 \oplus f(x)\rangle - |x\rangle \otimes |1 \oplus f(x)\rangle}{\sqrt{2}} \\
&= \frac{|x\rangle \otimes |f(x)\rangle - |x\rangle \otimes |\overline{f(x)}\rangle}{\sqrt{2}} \\
&= |x\rangle \otimes \frac{|f(x)\rangle - |\overline{f(x)}\rangle}{\sqrt{2}} \\
\end{align}
$$
Because $\frac{|f(x)\rangle - |\overline{f(x)}\rangle}{\sqrt{2}}$ is either $\frac{|0\rangle - |1\rangle}{\sqrt{2}}$ or $\frac{|1\rangle - |0\rangle}{\sqrt{2}}$, $|\varphi_2\rangle $ could be further simplified as
$$
\begin{align}
|\varphi_2\rangle &= (-1)^{f(x)} |x\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}} \\
\end{align}
$$
The observation from the first qubit output is always the same to the first qubit input, whereas there are 50-50 percent chance observing 0 or 1 for the second qubit.
This provides no information of determining whether $f(x)$ is constant or balanced either.
Third Attempt
In the third attempt, we made the both qubit inputs to $U_f$ superpositions. The superpositions for the first qubit and the second qubit are $H|0\rangle$ and $H|1\rangle$, respectively.
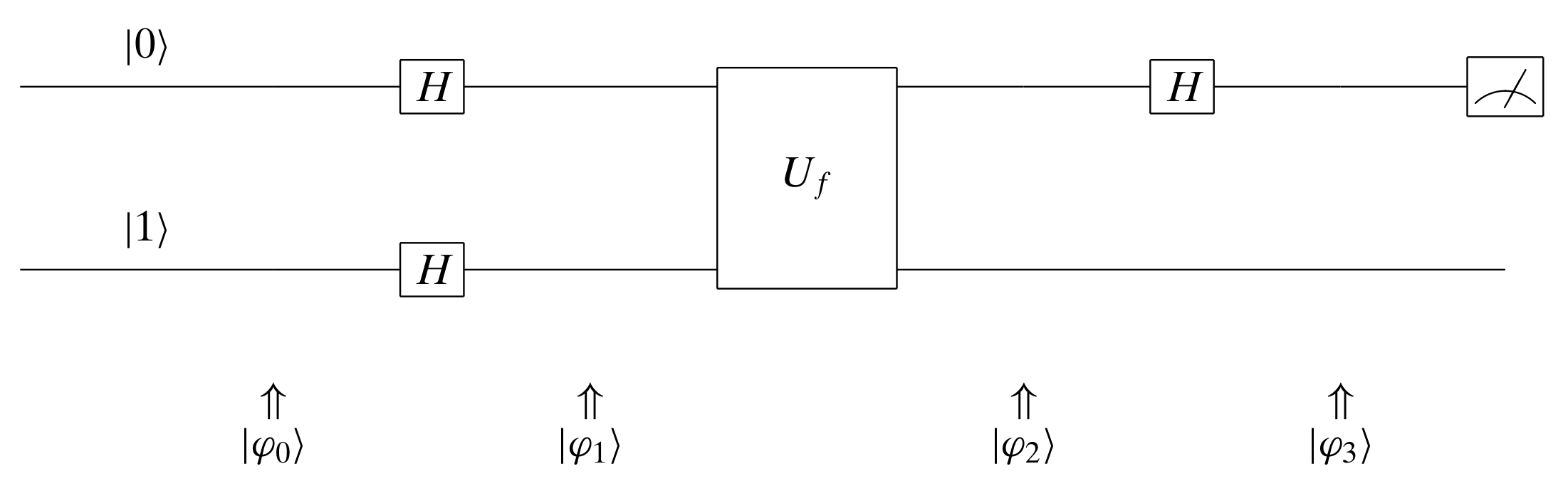
$$
\begin{align}
|\varphi_0\rangle &= |0\rangle \otimes |1\rangle\\
&= |0, 1\rangle \\
\end{align}
$$
$$
\begin{align}
|\varphi_1\rangle &= (H \otimes H) |\varphi_0\rangle \\
&= (H \otimes H) (|0\rangle \otimes |1\rangle) \\
&= H|0\rangle \otimes H |1\rangle \\
&= \frac{|0\rangle + |1\rangle}{\sqrt{2}} \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}} \\
&= \frac{|0, 0\rangle - |0, 1\rangle + |1, 0\rangle - |1, 1\rangle}{2} \\
\end{align}
$$
$$
\begin{align}
|\varphi_2\rangle &= U_f |\varphi_1\rangle \\
&= U_f \frac{|0, 0\rangle - |0, 1\rangle + |1, 0\rangle - |1, 1\rangle}{2} \\
&= \frac{1}{\sqrt{2}} U_f \frac{|0, 0\rangle - |0, 1\rangle + |1, 0\rangle - |1, 1\rangle}{\sqrt{2}} \\
&= \frac{1}{\sqrt{2}} \Big[ U_f \frac{|0, 0\rangle - |0, 1\rangle}{\sqrt{2}} + U_f \frac{|1, 0\rangle - |1, 1\rangle}{\sqrt{2}} \Big]\\
&= \frac{1}{\sqrt{2}} \Big[ (-1)^{f(0)} |0\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}} + (-1)^{f(1)} |1\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}} \Big]\\
&= \frac{1}{2} \Big[ (-1)^{f(0)} |0\rangle \otimes (|0\rangle - |1\rangle) + (-1)^{f(1)} |1\rangle \otimes (|0\rangle - |1\rangle) \Big]\\
&= \frac{1}{2} (-1)^{f(0)} \Big[ |0\rangle \otimes (|0\rangle - |1\rangle) + (-1)^{f(1) - f(0)} |1\rangle \otimes (|0\rangle - |1\rangle) \Big]\\
&= \frac{1}{2} (-1)^{f(0)} \Big[ |0\rangle \otimes (|0\rangle - |1\rangle) + (-1)^{f(0) \oplus f(1)} |1\rangle \otimes (|0\rangle - |1\rangle) \Big]\\
&= \frac{1}{2} (-1)^{f(0)} \Big[ \big(|0\rangle + (-1)^{f(0) \oplus f(1)} |1\rangle \big) \otimes (|0\rangle - |1\rangle) \Big]\\
\end{align}
$$
Note that if $f(0) \oplus f(1) = 0$, $f(x)$ is constant; if $f(0) \oplus f(1) = 1$, $f(x)$ is balanced. This information is encoded in the phase of the first qubit. How could we extract this key information?
We noticed that in the first qubit output $|0\rangle + (-1)^{f(0) \oplus f(1)} |1\rangle$ is either $|0\rangle + |1\rangle$ when $f(0) \oplus f(1) = 0$ or $|0\rangle - |1\rangle$ when $f(0) \oplus f(1) = 1$. Applying a Hadamard operator to it results in $|0\rangle$ when $f(0) \oplus f(1) = 0$ or $|1\rangle$ when $f(0) \oplus f(1) = 1$.
This means if $f(x)$ is constant, we must observe 0 for the first qubit whereas if $f(x)$ is balanced, we must observe 1 for the first qubit. Therefore, we are able to determine if $f(x)$ is constant or balanced using such quantum circuits.
Final Remarks
Conventionally, we compare algorithms on the same platform, either it is a classical computer or a quantum computer. However, in our case, it is a little bit weird that the classical algorithm is using classical gate whereas the quantum algorithm uses quantum gate, yet we still have to compare the two algorithms. Therefore, in my opinion, such comparison is not fair.
##S References
Deutsch's Algorithm