Axis/Angle 3D Rotation Representation
Introduction
Previously, we have systematically discussed about the 2D plane transformations. The 3D transformation, the 3D rotation in particular, is not as straightforward as the 2D rotation.
In this blog post, I would like to derive the 3D rotation matrix used for axis/angle rotation representation mathematically.
Prerequisites
Dot Product to Matrix Multiplication
Suppose $\mathbf{a}$ and $\mathbf{b}$ are both column vectors, we have the following property.
$$
\mathbf{b} (\mathbf{b} \cdot \mathbf{a}) = (\mathbf{b} \mathbf{b}^{\top}) \mathbf{a}
$$
Proof
$$
\begin{align}
\mathbf{b} (\mathbf{b} \cdot \mathbf{a}) &= \mathbf{b} (\mathbf{b}^{\top} \mathbf{a}) \\
&= (\mathbf{b} \mathbf{b}^{\top}) \mathbf{a} \\
\end{align}
$$
Cross Product
The cross product is defined by the formula
$$
\mathbf{a} \times \mathbf{b} = \lVert \mathbf{a} \rVert \lVert \mathbf{b} \rVert (\sin \theta) \mathbf{n}
$$
- $\theta$ is the angle between $\mathbf{a}$ and $\mathbf{b}$ in the plane containing them (hence, it is between 0° and 180°).
- $\lVert \mathbf{a} \rVert $ and $\lVert \mathbf{b} \rVert$ are the magnitudes of vectors $\mathbf{a}$ and $\mathbf{b}$.
- $\mathbf{n}$ is a unit vector perpendicular to the plane containing $\mathbf{a}$ and $\mathbf{b}$, in the direction given by the right-hand rule.
If $\theta = 90°$ and $\lVert \mathbf{b} \rVert = 1$, the cross product of $\mathbf{a}$ and $\mathbf{b}$ is just rotating $\mathbf{a}$ around $\mathbf{b}$ for 90°.
$$
\mathbf{a} \times \mathbf{b} = \lVert \mathbf{a} \rVert \mathbf{n}
$$
Cross Product Matrix Multiplication Form
As we have discussed in my previous blog post “Geometry for Computing Dihedral Angles”, we could express the vector cross product using matrix multiplication.
Suppose $\mathbf{u} = [u_1, u_2, u_3]$ and $\mathbf{v} = [v_1, v_2, v_3]$ are column vectors, we have the matrix multiplication expression.
$$
\begin{align}
\mathbf{u} \times \mathbf{v}
&= [\mathbf{u}]_{\times} \mathbf{v} \\
&= -[\mathbf{v}]_{\times} \mathbf{u} \\
\end{align}
$$
where
$$
[\mathbf{u}]_{\times} =
\begin{bmatrix}
0 & -u_3 & u_2 \\
u_3 & 0 & -u_1 \\
-u_2 & u_1 & 0 \\
\end{bmatrix}
$$
and
$$
[\mathbf{v}]_{\times} =
\begin{bmatrix}
0 & -v_3 & v_2 \\
v_3 & 0 & -v_1 \\
-v_2 & v_1 & 0 \\
\end{bmatrix}
$$
3D Rotation Matrix
Rodriguez’s Formula
A rotation could be represented by a rotation axis $\hat{\mathbf{n}}$, where $\hat{\mathbf{n}} = (\hat{n}_1, \hat{n}_2, \hat{n}_3)$ is a unit vector, and an angle $\theta$.
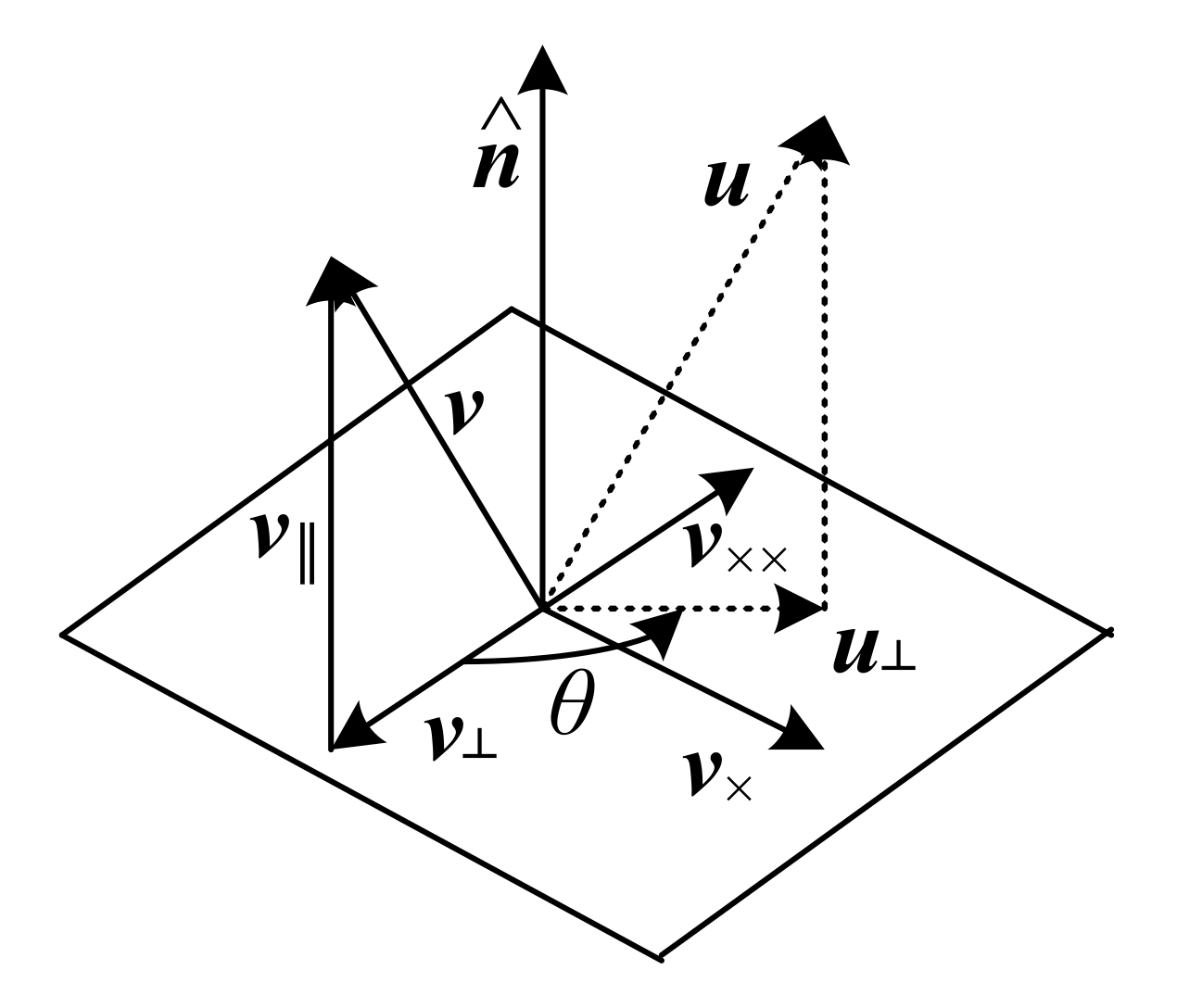
Because
$$
\hat{\mathbf{n}} \cdot \mathbf{v} = \lVert \hat{\mathbf{n}} \rVert \lVert \mathbf{v} \rVert \cos \phi
$$
and
$$
\lVert \hat{\mathbf{n}} \rVert = 1
$$
We have
$$
\begin{align}
\mathbf{v}_{\parallel} &= \frac{\hat{\mathbf{n}}}{\lVert \hat{\mathbf{n}} \rVert} \lVert \mathbf{v} \rVert \cos \phi \\
&= \frac{\hat{\mathbf{n}}}{\lVert \hat{\mathbf{n}} \rVert} \frac{\hat{\mathbf{n}} \cdot \mathbf{v}}{\lVert \hat{\mathbf{n}} \rVert} \\
&= \hat{\mathbf{n}} ( \hat{\mathbf{n}} \cdot \mathbf{v} ) \\
&= \hat{\mathbf{n}} ( \hat{\mathbf{n}}^{\top} \mathbf{v} ) \\
&= (\hat{\mathbf{n}} \hat{\mathbf{n}}^{\top})\mathbf{v} \\
\end{align}
$$
$$
\begin{align}
\mathbf{v}_{\bot} &= \mathbf{v} - \mathbf{v}_{\parallel} \\
&= \mathbf{I} \mathbf{v} - (\hat{\mathbf{n}} \hat{\mathbf{n}}^{\top})\mathbf{v} \\
&= (\mathbf{I} - \hat{\mathbf{n}} \hat{\mathbf{n}}^{\top})\mathbf{v} \\
\end{align}
$$
$\mathbf{v}_{\times}$ is the vector of rotating $\mathbf{v}_{\bot}$ around $\hat{\mathbf{n}}$ for 90° and is perpendicular to the $\hat{\mathbf{n}}$ and $\mathbf{v}_{\bot}$. It can be computed using the cross product of the unit vector $\hat{\mathbf{n}}$ and $\mathbf{v}$.
$$
\begin{align}
\mathbf{v}_{\times} &= \hat{\mathbf{n}} \times \mathbf{v} \\
&= [\hat{\mathbf{n}}]_{\times} \mathbf{v}
\end{align}
$$
where
$$
[\hat{\mathbf{n}}]_{\times} =
\begin{bmatrix}
0 & -\hat{n}_3 & \hat{n}_2 \\
\hat{n}_3 & 0 & -\hat{n}_1 \\
-\hat{n}_2 & \hat{n}_1 & 0 \\
\end{bmatrix}
$$
$\mathbf{v}_{\times\times}$ is the vector of rotating $\mathbf{v}_{\times}$ around $\hat{\mathbf{n}}$ for 90° and is perpendicular to the $\hat{\mathbf{n}}$ and $\mathbf{v}_{\times}$. It can be computed using the cross product of the unit vector $\hat{\mathbf{n}}$ and $\mathbf{v}_{\times}$.
$$
\begin{align}
\mathbf{v}_{\times\times} &= \hat{\mathbf{n}} \times \mathbf{v}_{\times} \\
&= [\hat{\mathbf{n}}]_{\times} \mathbf{v}_{\times} \\
&= [\hat{\mathbf{n}}]_{\times} ([\hat{\mathbf{n}}]_{\times} \mathbf{v}) \\
&= [\hat{\mathbf{n}}]_{\times}^2 \mathbf{v} \\
\end{align}
$$
Notice that
$$
\lVert \mathbf{v}_{\bot} \rVert = \lVert \mathbf{v}_{\times} \rVert = \lVert \mathbf{v}_{\times\times} \rVert
$$
and
$$
\begin{align}
\mathbf{v}_{\bot} &= - \mathbf{v}_{\times\times} \\
&= - [\hat{\mathbf{n}}]_{\times}^2 \mathbf{v} \\
\end{align}
$$
Thus,
$$
\begin{align}
\mathbf{v}_{\parallel} &= \mathbf{v} - \mathbf{v}_{\bot} \\
&= \mathbf{v} + [\hat{\mathbf{n}}]_{\times}^2 \mathbf{v} \\
&= (\mathbf{I} + [\hat{\mathbf{n}}]_{\times}^2) \mathbf{v} \\
\end{align}
$$
The projection of the rotated vector $\mathbf{u}$ on the plane of $\mathbf{v}_{\bot}$ and $\mathbf{v}_{\times}$, $\mathbf{u}_{\bot}$ is
$$
\begin{align}
\mathbf{u}_{\bot} &= \mathbf{v}_{\bot} \cos \theta + \mathbf{v}_{\times} \sin \theta \\
&= (- [\hat{\mathbf{n}}]_{\times}^2 \mathbf{v}) \cos \theta + ([\hat{\mathbf{n}}]_{\times} \mathbf{v}) \sin \theta \\
&= ( [\hat{\mathbf{n}}]_{\times} \sin \theta - [\hat{\mathbf{n}}]_{\times}^2 \cos \theta ) \mathbf{v} \\
\end{align}
$$
Therefore,
$$
\begin{align}
\mathbf{u} &= \mathbf{u}_{\bot} + \mathbf{v}_{\parallel} \\
&= ( [\hat{\mathbf{n}}]_{\times} \sin \theta - [\hat{\mathbf{n}}]_{\times}^2 \cos \theta ) \mathbf{v} + (\mathbf{I} + [\hat{\mathbf{n}}]_{\times}^2) \mathbf{v} \\
&= \big( \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \big) \mathbf{v} \\
\end{align}
$$
The 3D rotation matrix described by a rotation axis $\hat{\mathbf{n}}$, where $\hat{\mathbf{n}}$ is a unit vector, and an angle $\theta$ is
$$
\mathbf{R}(\hat{\mathbf{n}}, \theta) = \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta )
$$
which is known as the Rodriguez’s formula.
Rodriguez’s Formula Via Exponential Twist
There is a more convenient and elegant way to obtain the Rodriguez’s Formula, called exponential twist. Consider we move the vector $\mathbf{v}$ around the rotation axis $\hat{\mathbf{n}}$ for an extremely small angle $\varphi$, the resulting vector $\mathbf{v}^{\prime}$ will be
$$
\begin{align}
\mathbf{v}^{\prime} &= \mathbf{v} + \mathbf{v}_{\times} \sin \varphi \\
&= \mathbf{v} + [\hat{\mathbf{n}}]_{\times} \mathbf{v} \sin \varphi \\
&= \mathbf{v} + [\hat{\mathbf{n}}]_{\times} \mathbf{v} \varphi \\
&= (\mathbf{I} + \varphi [\hat{\mathbf{n}}]_{\times}) \mathbf{v}\\
\end{align}
$$
Therefore, the vector $\mathbf{u}$ after rotating the vector $\mathbf{v}$ around the rotation axis $\hat{\mathbf{n}}$ for angle $\theta$ is
$$
\begin{align}
\mathbf{u} &= \lim_{k\to\infty} (\mathbf{I} + \frac{\theta}{k} [\hat{\mathbf{n}}]_{\times})^k \mathbf{v} \\
&= \lim_{k\to\infty} (\mathbf{I} + \frac{\theta [\hat{\mathbf{n}}]_{\times}}{k})^k \mathbf{v} \\
&= \mathbf{R}(\hat{\mathbf{n}}, \theta) \mathbf{v} \\
\end{align}
$$
By the limit definition of matrix exponential,
$$
\begin{align}
\exp ( \theta [\hat{\mathbf{n}}]_{\times} ) &= \lim_{k\to\infty} (\mathbf{I} + \frac{\theta [\hat{\mathbf{n}}]_{\times}}{k})^k \\
\end{align}
$$
We further expand the matrix exponential using the series definition of matrix exponential,
$$
\begin{align}
\exp ( \theta [\hat{\mathbf{n}}]_{\times} ) &= \sum_{k=0}^{\infty} \frac{(\theta [\hat{\mathbf{n}}]_{\times})^k}{k!} \\
&= I + \theta [\hat{\mathbf{n}}]_{\times} + \frac{\theta^2}{2} [\hat{\mathbf{n}}]_{\times}^2 + \frac{\theta^3}{3} [\hat{\mathbf{n}}]_{\times}^3 + \cdots \\
\end{align}
$$
Because
$$
\begin{align}
\hat{\mathbf{n}} \times (\hat{\mathbf{n}} \times \mathbf{v}_{\bot})
&= [\hat{\mathbf{n}}]_{\times} ([\hat{\mathbf{n}}]_{\times} \mathbf{v}_{\bot}) \\
&= [\hat{\mathbf{n}}]_{\times}^2 \mathbf{v}_{\bot} \\
&= - \mathbf{v}_{\bot} \\
\end{align}
$$
We have
$$
\begin{align}
[\hat{\mathbf{n}}]_{\times}^2 &= - \mathbf{I} \\
\end{align}
$$
Thus, $\mathbf{R}(\hat{\mathbf{n}}, \theta)$ becomes
$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, \theta) &= \lim_{k\to\infty} (\mathbf{I} + \frac{\theta [\hat{\mathbf{n}}]_{\times}}{k})^k \\
&= \exp ( \theta [\hat{\mathbf{n}}]_{\times} ) \\
&= I + \theta [\hat{\mathbf{n}}]_{\times} + \frac{\theta^2}{2} [\hat{\mathbf{n}}]_{\times}^2 + \frac{\theta^3}{3} [\hat{\mathbf{n}}]_{\times}^3 + \cdots \\
&= I + (\theta - \frac{\theta^3}{3} + \frac{\theta^5}{5} - \cdots) [\hat{\mathbf{n}}]_{\times} + (\frac{\theta^2}{2} - \frac{\theta^4}{4} + \frac{\theta^6}{6} - \cdots) [\hat{\mathbf{n}}]_{\times}^2 \\
\end{align}
$$
Notice that the Taylor series for $\sin \theta$ and $\cos \theta$ evaluated at 0 are
$$
\sin \theta = \theta - \frac{\theta^3}{3} + \frac{\theta^5}{5} - \cdots
$$
and
$$
\cos \theta = 1 - \frac{\theta^2}{2} + \frac{\theta^4}{4} - \frac{\theta^6}{6} + \cdots
$$
Therefore,
$$
\mathbf{R}(\hat{\mathbf{n}}, \theta) = \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta )
$$
We derived the Rodriguez’s formula again via exponential twist.
Rodriguez’s Formula Properties
It is easy to find that when $\theta = 0$
$$
\mathbf{R}(\hat{\mathbf{n}}, 0) = \mathbf{I}
$$
In addition, we should expect that
$$
\mathbf{R}(\hat{\mathbf{n}}, \theta) \mathbf{R}(\hat{\mathbf{n}}, - \theta) = \mathbf{I}
$$
Let’s verify this property.
$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, \theta) \mathbf{R}(\hat{\mathbf{n}}, - \theta) &= \left( \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \right) \left( \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin (-\theta) + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos (-\theta) ) \right) \\
&= \left( \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \right) \left( \mathbf{I} - [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \right) \\
&= \mathbf{I} + [\hat{\mathbf{n}}]_{\times}^2 (\cos \theta - 1)^2 + [\hat{\mathbf{n}}]_{\times}^4 (\cos \theta - 1)^2 \\
&= \mathbf{I} + [\hat{\mathbf{n}}]_{\times}^2 \left( [\hat{\mathbf{n}}]_{\times}^2 + \mathbf{I} \right) (\cos \theta - 1)^2 \\
\end{align}
$$
Because
$$
\begin{align}
[\hat{\mathbf{n}}]_{\times}^2
&=
\begin{bmatrix}
0 & -\hat{n}_3 & \hat{n}_2 \\
\hat{n}_3 & 0 & -\hat{n}_1 \\
-\hat{n}_2 & \hat{n}_1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
0 & -\hat{n}_3 & \hat{n}_2 \\
\hat{n}_3 & 0 & -\hat{n}_1 \\
-\hat{n}_2 & \hat{n}_1 & 0 \\
\end{bmatrix}
\\
&=
\begin{bmatrix}
-\hat{n}_3^2 -\hat{n}_2^2 & \hat{n}_1 \hat{n}_2 & \hat{n}_1 \hat{n}_3 \\
\hat{n}_1 \hat{n}_2 & -\hat{n}_3^2 -\hat{n}_1^2 & \hat{n}_2 \hat{n}_3 \\
\hat{n}_1 \hat{n}_3 & \hat{n}_2 \hat{n}_3 & -\hat{n}_2^2 -\hat{n}_1^2 \\
\end{bmatrix}
\end{align}
$$
$$
\begin{align}
[\hat{\mathbf{n}}]_{\times}^2 + \mathbf{I}
&=
\begin{bmatrix}
1 -\hat{n}_3^2 -\hat{n}_2^2 & \hat{n}_1 \hat{n}_2 & \hat{n}_1 \hat{n}_3 \\
\hat{n}_1 \hat{n}_2 & 1 -\hat{n}_3^2 -\hat{n}_1^2 & \hat{n}_2 \hat{n}_3 \\
\hat{n}_1 \hat{n}_3 & \hat{n}_2 \hat{n}_3 & 1 -\hat{n}_2^2 -\hat{n}_1^2 \\
\end{bmatrix}
\\
&=
\begin{bmatrix}
\hat{n}_1^2 & \hat{n}_1 \hat{n}_2 & \hat{n}_1 \hat{n}_3 \\
\hat{n}_1 \hat{n}_2 & \hat{n}_2^2 & \hat{n}_2 \hat{n}_3 \\
\hat{n}_1 \hat{n}_3 & \hat{n}_2 \hat{n}_3 & \hat{n}_3^2 \\
\end{bmatrix}
\\
\end{align}
$$
$$
\begin{align}
[\hat{\mathbf{n}}]_{\times}^2 \left( [\hat{\mathbf{n}}]_{\times}^2 + \mathbf{I} \right)
&=
\begin{bmatrix}
-\hat{n}_3^2 -\hat{n}_2^2 & \hat{n}_1 \hat{n}_2 & \hat{n}_1 \hat{n}_3 \\
\hat{n}_1 \hat{n}_2 & -\hat{n}_3^2 -\hat{n}_1^2 & \hat{n}_2 \hat{n}_3 \\
\hat{n}_1 \hat{n}_3 & \hat{n}_2 \hat{n}_3 & -\hat{n}_2^2 -\hat{n}_1^2 \\
\end{bmatrix}
\begin{bmatrix}
\hat{n}_1^2 & \hat{n}_1 \hat{n}_2 & \hat{n}_1 \hat{n}_3 \\
\hat{n}_1 \hat{n}_2 & \hat{n}_2^2 & \hat{n}_2 \hat{n}_3 \\
\hat{n}_1 \hat{n}_3 & \hat{n}_2 \hat{n}_3 & \hat{n}_3^2 \\
\end{bmatrix}
\\
&= \mathbf{0} \\
\end{align}
$$
Therefore,
$$
\mathbf{R}(\hat{\mathbf{n}}, \theta) \mathbf{R}(\hat{\mathbf{n}}, - \theta) = \mathbf{I}
$$
Similarly, we should also expect that $\mathbf{R}(\hat{\mathbf{n}}, - \theta) = \mathbf{R}(- \hat{\mathbf{n}}, \theta)$.
$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, - \theta) &= \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin (-\theta) + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos (-\theta) ) \\
&= \mathbf{I} - [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \\
\end{align}
$$
$$
\begin{align}
\mathbf{R}(- \hat{\mathbf{n}}, \theta) &= \mathbf{I} - [\hat{\mathbf{n}}]_{\times} \sin \theta + \left([-\hat{\mathbf{n}}]_{\times}\right)^2 (1 - \cos \theta ) \\
&= \mathbf{I} - [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \\
\end{align}
$$
Therefore,
$$
\mathbf{R}(\hat{\mathbf{n}}, - \theta) = \mathbf{R}(- \hat{\mathbf{n}}, \theta)
$$
It is also not too difficult to find that $\mathbf{R}(\hat{\mathbf{n}}, - \theta) = \mathbf{R}(\hat{\mathbf{n}}, \theta)^{\top}$.
$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, \theta)^{\top} &= \left( \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \right)^{\top} \\
&= \mathbf{I}^{\top} + [\hat{\mathbf{n}}]_{\times}^{\top} \sin \theta + \left([\hat{\mathbf{n}}]_{\times}^2\right)^{\top} (1 - \cos \theta ) \\
&= \mathbf{I}^{\top} - [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \\
&= \mathbf{R}(\hat{\mathbf{n}}, - \theta) \\
\end{align}
$$
Taken together, similar to 2D rotation matrix, 3D rotation matrix is also orthonormal.
$$
\mathbf{R}(\hat{\mathbf{n}}, \theta)^{\top} = \mathbf{R}(\hat{\mathbf{n}}, \theta)^{-1} = \mathbf{R}(\hat{\mathbf{n}}, - \theta) = \mathbf{R}(- \hat{\mathbf{n}}, \theta)
$$
Small Angle Approximation
When $\theta$ is small, according to the small angle approximation, $\sin \theta = \theta$ and $\cos \theta = 1$.
We define
$$
\begin{align}
\mathbf{\omega} &= \theta \hat{\mathbf{n}} \\
&= (\theta \hat{n}_1, \theta \hat{n}_2, \theta \hat{n}_3) \\
&= (\omega_1, \omega_2, \omega_3) \\
\end{align}
$$
Thus, we have
$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, \theta) &= \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta - [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \\
&= \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \theta \\
&= \mathbf{I} + [\theta \hat{\mathbf{n}}]_{\times} \\
&= \mathbf{I} + [\mathbf{\omega}]_{\times} \\
&=
\begin{bmatrix}
1 & -\theta \hat{n}_3 & \theta \hat{n}_2 \\
\theta \hat{n}_3 & 1 & -\theta \hat{n}_1 \\
-\theta \hat{n}_2 & \theta \hat{n}_1 & 1 \\
\end{bmatrix} \\
&=
\begin{bmatrix}
1 & -\omega_3 & \omega_2 \\
\omega_3 & 1 & -\omega_1 \\
-\omega_2 & \omega_1 & 1 \\
\end{bmatrix} \\
&= \mathbf{R}(\mathbf{\omega})
\end{align}
$$
In this scenario, the rotation becomes
$$
\begin{align}
\mathbf{u} &= \mathbf{R}(\mathbf{\omega}) \mathbf{v} \\
&= (\mathbf{I} + [\mathbf{\omega}]_{\times}) \mathbf{v} \\
&= \mathbf{v} + [\mathbf{\omega}]_{\times} \mathbf{v} \\
&= \mathbf{v} - [\mathbf{v}]_{\times} \mathbf{\omega} \\
&= \mathbf{v} + \mathbf{\omega} \times \mathbf{v} \\
\end{align}
$$
Computing the derivatives are also simple since we have the matrix multiplication form.
$$
\begin{align}
\frac{\partial \mathbf{u}}{\mathbf{v}} = \mathbf{R}(\mathbf{\omega}) \\
\end{align}
$$
and
$$
\begin{align}
\frac{\partial \mathbf{u}}{\mathbf{\omega}} = - [\mathbf{v}]_{\times} \\
\end{align}
$$
Miscellaneous
The rotation representation using the axis coordinates and angle information directly is called “axis/angle representation”. There are other rotation representations, such as “unit quaternion”, which we will discuss later in other articles.
References
Axis/Angle 3D Rotation Representation