Unit Quaternion 3D Rotation Representation

Introduction

In my previous article “Axis/Angle 3D Rotation Representation”, we have learned the axis/angle 3D rotation representation, there is another commonly used representation which is called unit quaternion 3D rotation representation.

In this blog post, I would like to discuss the quaternion 3D rotation representation and derive some of its properties mathematically.

Axis/Angle Rotation Representation

Here is a quick recovery from my previous article “Axis/Angle 3D Rotation Representation” on the axis/angle rotation representation.

$$
\mathbf{R}(\hat{\mathbf{n}}, \theta) = \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta )
$$

where the unit rotation vector $\hat{\mathbf{n}} = (\hat{n}_1, \hat{n}_2, \hat{n}_3)$ and $\lVert \hat{\mathbf{n}} \rVert = \sqrt{\hat{n}_1^2 + \hat{n}_2^2 + \hat{n}_3^2} = 1$ and

$$
[\hat{\mathbf{n}}]_{\times} =
\begin{bmatrix}
0 & -\hat{n}_3 & \hat{n}_2 \\
\hat{n}_3 & 0 & -\hat{n}_1 \\
-\hat{n}_2 & \hat{n}_1 & 0 \\
\end{bmatrix}
$$

Quaternion Rotation Representation

The quaternion rotation representation is closely related to the axis/angle rotation representation. The two representations could be converted from each other.

$$
\begin{align}
\mathbf{q} &= \left(x, y, z, w\right) \\
&= \left(\mathbf{v}, w\right) \\
&= \left(\hat{\mathbf{n}} \sin \frac{\theta}{2}, \cos \frac{\theta}{2}\right) \\
&= \left(\hat{n}_1 \sin \frac{\theta}{2}, \hat{n}_2 \sin \frac{\theta}{2}, \hat{n}_3 \sin \frac{\theta}{2}, \cos \frac{\theta}{2}\right) \\
\end{align}
$$

where

$$
\begin{align}
x &= \hat{n}_1 \sin \frac{\theta}{2} \\
y &= \hat{n}_2 \sin \frac{\theta}{2} \\
z &= \hat{n}_3 \sin \frac{\theta}{2} \\
w &= \cos \frac{\theta}{2} \\
\end{align}
$$

It is easy to verify that $\mathbf{q}$ is a unit vector.

$$
\begin{align}
\lVert \mathbf{q} \rVert &= \sqrt{\lVert \hat{\mathbf{n}} \rVert^2 \sin^2 \frac{\theta}{2} + \cos^2 \frac{\theta}{2}} \\
&= \sqrt{\sin^2 \frac{\theta}{2} + \cos^2 \frac{\theta}{2}} \\
&= 1
\end{align}
$$

Because $\sin \theta = 2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}$ and $1 - \cos \theta = 2 \sin^2 \frac{\theta}{2}$,

$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, \theta) &= \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \sin \theta + [\hat{\mathbf{n}}]_{\times}^2 (1 - \cos \theta ) \\
&= \mathbf{I} + [\hat{\mathbf{n}}]_{\times} \left( 2 \sin \frac{\theta}{2} \cos \frac{\theta}{2} \right) + [\hat{\mathbf{n}}]_{\times}^2 \left( 2 \sin^2 \frac{\theta}{2} \right) \\
&= \mathbf{I} + 2w \left( [\hat{\mathbf{n}}]_{\times} \sin \frac{\theta}{2} \right) + 2 \left( [\hat{\mathbf{n}}]_{\times} \sin \frac{\theta}{2} \right)^2 \\
\end{align}
$$

We define a new matrix $[\hat{\mathbf{v}}]_{\times}$,

$$
\begin{align}
[\hat{\mathbf{v}}]_{\times} &= [\hat{\mathbf{n}}]_{\times} \sin \frac{\theta}{2} \\
&=
\begin{bmatrix}
0 & -\hat{n}_3 \sin \frac{\theta}{2} & \hat{n}_2 \sin \frac{\theta}{2} \\
\hat{n}_3 \sin \frac{\theta}{2} & 0 & -\hat{n}_1 \sin \frac{\theta}{2} \\
-\hat{n}_2 \sin \frac{\theta}{2} & \hat{n}_1 \sin \frac{\theta}{2} & 0 \\
\end{bmatrix} \\
&=
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0 \\
\end{bmatrix} \\
\end{align}
$$

Thus,

$$
\begin{align}
[\hat{\mathbf{v}}]_{\times}^2 &=
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0 \\
\end{bmatrix}
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0 \\
\end{bmatrix}
\\
&=
\begin{bmatrix}
-y^2 - z^2 & xy & xz \\
xy & -x^2 - z^2 & yz \\
xz & yz & -x^2 - y^2 \\
\end{bmatrix}
\\
\end{align}
$$

Therefore, the rotation matrix could be expressed using $\mathbf{q} = (x, y, z, w)$.

$$
\begin{align}
\mathbf{R}(\hat{\mathbf{n}}, \theta)
&= \mathbf{I} + 2w \left( [\hat{\mathbf{n}}]_{\times} \sin \frac{\theta}{2} \right) + 2 \left( [\hat{\mathbf{n}}]_{\times} \sin \frac{\theta}{2} \right)^2 \\
&= \mathbf{I} + 2w [\hat{\mathbf{v}}]_{\times} + 2 [\hat{\mathbf{v}}]_{\times}^2 \\
&=
\begin{bmatrix}
1 - 2(y^2 + z^2) & 2(xy - zw) & 2(xz + yw) \\
2(xy + zw) & 1 - 2(x^2 + z^2) & 2(yz- xw) \\
2(xz - yw) & 2(yz + xw) & 1 - 2(x^2 + y^2) \\
\end{bmatrix}
\\
\end{align}
$$

Formally, the rotation matrix $\mathbf{R}(\mathbf{q})$ could be expressed as

$$
\begin{align}
\mathbf{R}(\mathbf{q})
&=
\begin{bmatrix}
1 - 2(y^2 + z^2) & 2(xy - zw) & 2(xz + yw) \\
2(xy + zw) & 1 - 2(x^2 + z^2) & 2(yz- xw) \\
2(xz - yw) & 2(yz + xw) & 1 - 2(x^2 + y^2) \\
\end{bmatrix}
\\
\end{align}
$$

Notice that

$$
\begin{align}
1 - 2(y^2 + z^2) &= \left( 1 - (y^2 + z^2) \right) - (y^2 + z^2) \\
&= \left( 1 - \sin^2 \frac{\theta}{2}(\hat{n}_2^2 + \hat{n}_3^2) \right) - (y^2 + z^2)\\
&= \left( 1 - \sin^2 \frac{\theta}{2}(1 - \hat{n}_1^2) \right) - (y^2 + z^2)\\
&= \left( 1 - \sin^2 \frac{\theta}{2} + \sin^2 \frac{\theta}{2} \hat{n}_1^2 \right) - (y^2 + z^2)\\
&= \left( \cos^2 \frac{\theta}{2} + \sin^2 \frac{\theta}{2} \hat{n}_1^2 \right) - (y^2 + z^2)\\
&= w^2 + x^2 - y^2 - z^2 \\
\end{align}
$$

Similarly,

$$
\begin{align}
1 - 2(x^2 + z^2)
&= w^2 + y^2 - x^2 - z^2 \\
\end{align}
$$

$$
\begin{align}
1 - 2(x^2 + y^2)
&= w^2 + z^2 - x^2 - y^2 \\
\end{align}
$$

So the rotation matrix $\mathbf{R}(\mathbf{q})$ could also be expressed as

$$
\begin{align}
\mathbf{R}(\mathbf{q})
&=
\begin{bmatrix}
w^2 + x^2 - y^2 - z^2 & 2(xy - zw) & 2(xz + yw) \\
2(xy + zw) & w^2 + y^2 - x^2 - z^2 & 2(yz- xw) \\
2(xz - yw) & 2(yz + xw) & w^2 + z^2 - x^2 - y^2 \\
\end{bmatrix}
\\
\end{align}
$$

Quaternion Algebra and Properties

Identity Quaternion

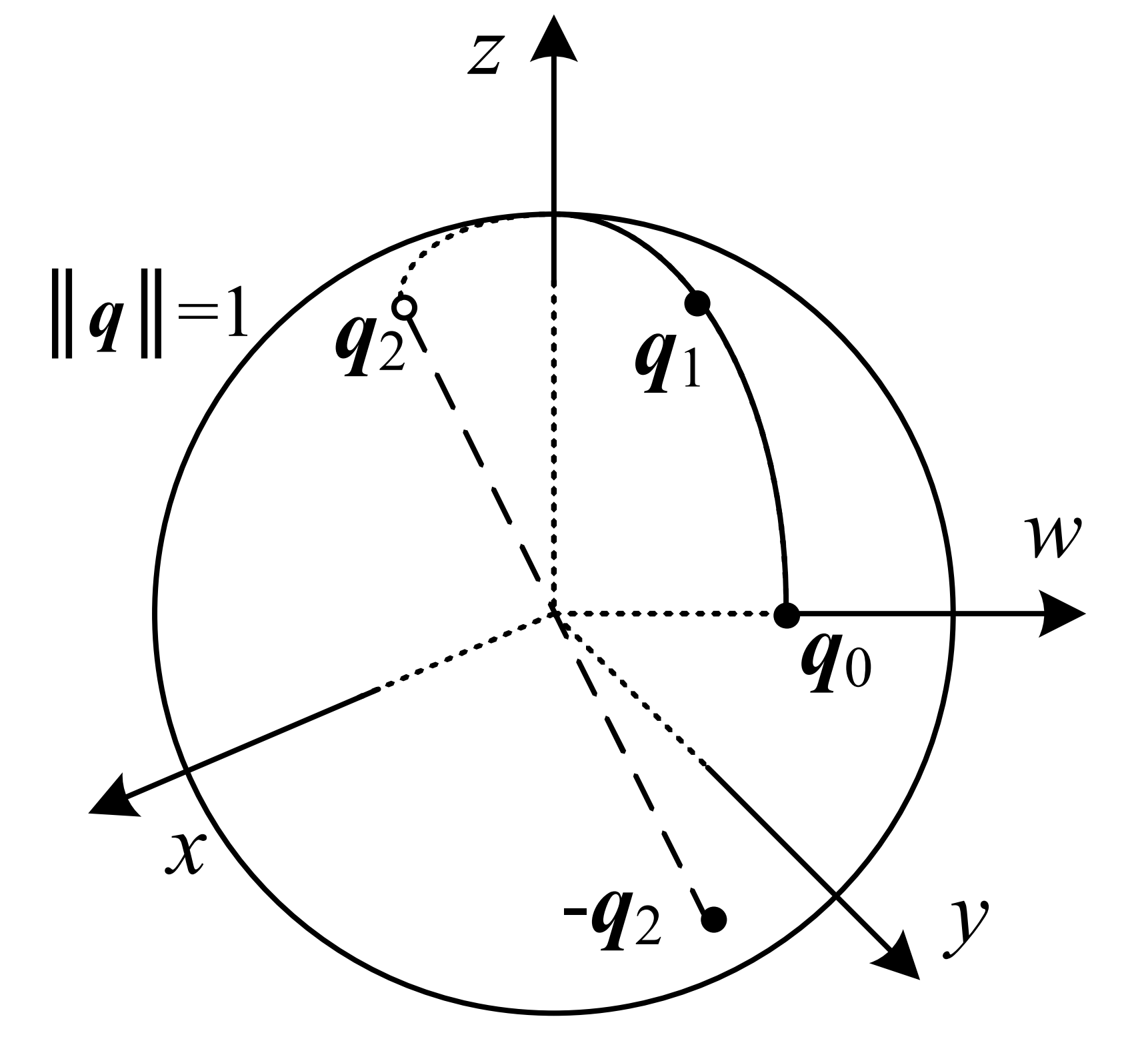
It is easy to find that the identity quaternion is $\mathbf{q} = (\mathbf{0}, 1) = (0, 0, 0, 1)$.

Antipodal Quaternion

Quaternion $\mathbf{q} = (\mathbf{v}, w) = (x, y, z, w)$ and its antipodal quaternion $-\mathbf{q} = (-\mathbf{v}, -w) = (-x, -y, -z, -w)$ represent the same rotation, because it is easy to find that the rotational matrices $\mathbf{R}(\mathbf{q})$ and $\mathbf{R}(-\mathbf{q})$ are exactly the same, i.e., $\mathbf{R}(\mathbf{q}) = \mathbf{R}(-\mathbf{q})$.

Quaternion Multiplication

Suppose $\mathbf{q}_0 = (\mathbf{v}_0, w_0) = (x_0, y_0, z_0, w_0)$, $\mathbf{q}_1 = (\mathbf{v}_1, w_1) = (x_1, y_1, z_1, w_1)$, $\mathbf{q}_2 = (\mathbf{v}_2, w_2) = (x_2, y_2, z_2, w_2)$, quaternion multiplication is defined as follows

$$
\begin{align}
\mathbf{q}_2
&= \mathbf{q}_0 \mathbf{q}_1 \\
&= \left(\mathbf{v}_0 \times \mathbf{v}_1 + w_0 \mathbf{v}_1 + w_1 \mathbf{v}_0, w_0 w_1 - \mathbf{v}_0 \mathbf{v}_1 \right) \\
\end{align}
$$

It carries the property that $\mathbf{R}(\mathbf{q}_2) = \mathbf{R}(\mathbf{q}_0) \mathbf{R}(\mathbf{q}_1)$, which means quaternion multiplication is just applying two rotations $\mathbf{q}_1$ and $\mathbf{q}_0$ sequentially (not $\mathbf{q}_0$ and $\mathbf{q}_1$!). The verification of this property is skipped in this article as the algebra is too complex.

Concretely,

$$
\begin{align}
\mathbf{q}_2
&= \mathbf{q}_0 \mathbf{q}_1 \\
&= \left(\mathbf{v}_0 \times \mathbf{v}_1 + w_0 \mathbf{v}_1 + w_1 \mathbf{v}_0, w_0 w_1 - \mathbf{v}_0 \mathbf{v}_1 \right) \\
&= ((y_0 z_1 - z_0 y_1, z_0 x_1 - x_0 z_1, x_0 y_1 - y_0 x_1) + (w_0 x_1, w_0 y_1, w_0 z_1) \\
&\quad + (w_1 x_0, w_1 y_0, w_1 z_0), w_0 w_1 - \left(x_0 x_1 + y_0 y_1 + z_0 z_1 \right) ) \\
&= (x_2, y_2, z_2, w_2) \\
\end{align}
$$

where

$$
\begin{align}
x_2 &= y_0 z_1 - z_0 y_1 + w_0 x_1 + w_1 x_0 \\
y_2 &= z_0 x_1 - x_0 z_1 + w_0 y_1 + w_1 y_0 \\
z_2 &= x_0 y_1 - y_0 x_1 + w_0 z_1 + w_1 z_0 \\
w_2 &= w_0 w_1 - x_0 x_1 - y_0 y_1 - z_0 z_1 \\
\end{align}
$$

Notice that quaternion Multiplication is not communicative, i.e., usually $\mathbf{q}_0 \mathbf{q}_1 \neq \mathbf{q}_1 \mathbf{q}_0$, simply because the rotation axis of the two rotations could be different. In addition, quaternion multiplication with identity quaternion does not change the quaternion, i.e., $\mathbf{q} \mathbf{q}_0 = \mathbf{q}_0 \mathbf{q} = \mathbf{q}$, when $\mathbf{q}_0 = (\mathbf{0}, 1)$.

Inverse Quaternion

Quaternion $\mathbf{q} = (\mathbf{v}, w) = (x, y, z, w)$ and its inverse quaternion $\mathbf{q}^{-1}$ cancel each other.

From my previous article “Axis/Angle 3D Rotation Representation”, we already know that $(\hat{\mathbf{n}}, - \theta)$ or $(-\hat{\mathbf{n}}, \theta)$ cancels $(\hat{\mathbf{n}}, \theta)$. Because the axis/angle representation $(\hat{\mathbf{n}}, \theta)$ corresponds to the quaternion representation $(\mathbf{v}, w) = (x, y, z, w)$, $(\hat{\mathbf{n}}, -\theta)$ corresponds to $(-\mathbf{v}, w) = (-x, -y, -z, w)$, $(-\hat{\mathbf{n}}, \theta)$ corresponds to $(-\mathbf{v}, w) = (-x, -y, -z, w)$, we could say $(-\mathbf{v}, w)$ cancels $(\mathbf{v}, w)$. Therefore, $\mathbf{q}^{-1} = (-\mathbf{v}, w) = (-x, -y, -z, w)$.

In fact, $(\hat{\mathbf{n}}, 2\pi - \theta)$ also cancels $(\hat{\mathbf{n}}, \theta)$, the axis/angle representation $(\hat{\mathbf{n}}, 2\pi - \theta)$ corresponds to the quaternion representation $(\mathbf{v}, -w) = (x, y, z, -w)$. Therefore, $\mathbf{q}^{-1} = (\mathbf{v}, -w) = (x, y, z, -w)$.

Taken together, there could be at least two expressions for the inverse quaternion $\mathbf{q}^{-1}$, $\mathbf{q}^{-1} = (\mathbf{v}, -w) = (x, y, z, -w)$ or $\mathbf{q}^{-1} = (-\mathbf{v}, w) = (-x, -y, -z, w)$.

Suppose we used the inverse quaternion expression $\mathbf{q}^{-1} = (\mathbf{v}, -w) = (x, y, z, -w)$, let’s verify if rotation $\mathbf{q}^{-1} = (x, y, z, -w)$ cancels rotation $\mathbf{q} = (\mathbf{v}, w) = (x, y, z, w)$.

$$
\begin{align}
\mathbf{R}(\mathbf{q}^{-1})
&=
\begin{bmatrix}
1 - 2(y^2 + z^2) & 2(xy + zw) & 2(xz - yw) \\
2(xy - zw) & 1 - 2(x^2 + z^2) & 2(yz + xw) \\
2(xz + yw) & 2(yz - xw) & 1 - 2(x^2 + y^2) \\
\end{bmatrix}
\\
&= \mathbf{R}(\mathbf{q})^{\top} \\
\end{align}
$$

From my previous article “Axis/Angle 3D Rotation Representation”, we can know that $\mathbf{R}(\mathbf{q})$ is orthonormal and $\mathbf{R}(\mathbf{q})^{\top} = \mathbf{R}(\mathbf{q})^{-1}$. Therefore,

$$
\mathbf{R}(\mathbf{q}^{-1}) = \mathbf{R}(\mathbf{q})^{\top} = \mathbf{R}(\mathbf{q})^{-1}
$$

So,

$$
\mathbf{R}(\mathbf{q}^{-1}) \mathbf{R}(\mathbf{q}) = \mathbf{I}
$$

Similarly, we could also show that rotation $\mathbf{q}^{-1} = (-\mathbf{v}, w) = (-x, -y, -z, w)$ cancels rotation $\mathbf{q} = (\mathbf{v}, w) = (x, y, z, w)$.

Notice that $\mathbf{q} \mathbf{q}^{-1} = \mathbf{q}^{-1} \mathbf{q} = (\mathbf{0}, 1) = (0, 0, 0, 1)$.

Quaternion Division

Suppose $\mathbf{q}_0 = (\mathbf{v}_0, w_0) = (x_0, y_0, z_0, w_0)$, $\mathbf{q}_1 = (\mathbf{v}_1, w_1) = (x_1, y_1, z_1, w_1)$, $\mathbf{q}_2 = (\mathbf{v}_2, w_2) = (x_2, y_2, z_2, w_2)$, quaternion division is defined as follows

$$
\begin{align}
\mathbf{q}_2
&= \frac{\mathbf{q}_0}{\mathbf{q}_1} \\
&= \mathbf{q}_0\mathbf{q}_1^{-1} \\
&= \left(\mathbf{v}_0 \times \mathbf{v}_1 + w_0 \mathbf{v}_1 - w_1 \mathbf{v}_0, - w_0 w_1 - \mathbf{v}_0 \mathbf{v}_1 \right) \\
&= \left(- \mathbf{v}_0 \times \mathbf{v}_1 - w_0 \mathbf{v}_1 + w_1 \mathbf{v}_0, w_0 w_1 + \mathbf{v}_0 \mathbf{v}_1 \right) \\
\end{align}
$$

Spherical Linear Interpolation

In some scenarios, we would like to compute a rotation that is in the pathway of two rotations. This procedure is called spherical linear interpolation or slerp for short.

Suppose we have two rotations using unit quaternion representation, $\mathbf{q}_0$ and $\mathbf{q}_1$, we would like to compute the rotation $\mathbf{q}_2$ that is $\alpha$ partway of the two rotations. The key to this procedure is to compute the rotation angle $\theta_r$ between the two rotations.

Suppose $\mathbf{q}_1 = \mathbf{q}_r \mathbf{q}_0$, i.e., $\mathbf{q}_1$ is applying $\mathbf{q}_0$ followed by $\mathbf{q}_r$, and $\mathbf{q}_2 = \mathbf{q}_\alpha \mathbf{q}_0$. Because

$$
\begin{align}
\mathbf{q}_1 \mathbf{q}_0^{-1} &= \mathbf{q}_r \mathbf{q}_0 \mathbf{q}_0^{-1} \\
&= \mathbf{q}_r (\mathbf{0}, 1) \\
&= \mathbf{q}_r \\
\end{align}
$$

Using quaternion division, we could compute $\mathbf{q}_r$,

$$
\begin{align}
\mathbf{q}_r &= \mathbf{q}_1 \mathbf{q}_0^{-1} = (\mathbf{v}_r, w_r)
\end{align}
$$

We want to make sure that $-\frac{\pi}{2} \leq \frac{\theta_r}{2} \leq \frac{\pi}{2}$, i.e., $w_r \geq 0$. There are chances $w_r < 0$, we could just apply the antipodal quaternion property and flip the quaternion $\mathbf{q}_r$, i.e., $\mathbf{q}_r \leftarrow - \mathbf{q}$. After all $\mathbf{q}_r$ and $-\mathbf{q}_r$ represent the same rotation.

Because $\lVert \mathbf{v}_r \rVert = \sin \frac{\theta_r}{2}$ and $w_r = \cos \frac{\theta_r}{2}$

$$
\begin{align}
\tan \frac{\theta_r}{2} &= \frac{\sin \frac{\theta_r}{2}}{\cos \frac{\theta_r}{2}} \\
&= \frac{\lVert \mathbf{v}_r \rVert}{w_r}
\end{align}
$$

$\theta_r$ could be computed using

$$
\begin{align}
\theta_r = 2 \arctan \left( \frac{\lVert \mathbf{v}_r \rVert}{w_r} \right)
\end{align}
$$

The fraction of the rotation angle $\theta_\alpha$ is therefore

$$
\theta_\alpha = \alpha \theta_r
$$

The unit rotation axis could also be computed using

$$
\begin{align}
\hat{\mathbf{n}}_r &= (\hat{n}_{r,1}, \hat{n}_{r,2}, \hat{n}_{r,3}) \\
&= \frac{\left( \hat{n}_{r,1} \sin \frac{\theta_r}{2}, \hat{n}_{r,2} \sin \frac{\theta_r}{2}, \hat{n}_{r,3} \sin \frac{\theta_r}{2} \right)}{\sin \frac{\theta_r}{2}} \\
&= \frac{\mathbf{v}_r}{\lVert \mathbf{v}_r \rVert} \\
\end{align}
$$

Thus, by the definition of quaternion,

$$
\mathbf{q}_\alpha = \left( \hat{\mathbf{n}}_r \sin \frac{\theta_\alpha}{2}, \cos \frac{\theta_\alpha}{2} \right)
$$

$$
\mathbf{q}_2 = \mathbf{q}_\alpha \mathbf{q}_0
$$